人教版九年级上册数学第22章二次函数复习课件(36张)
文档属性
| 名称 | 人教版九年级上册数学第22章二次函数复习课件(36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览










文档简介
(共36张PPT)
二次函数的总结与复习
学习目标
复习二次函数的相关知识点
提高用二次函数的相关知识点解决问题的能力
形如
(a、b、c是常数,a≠0)的函数叫做
x
的二次函数,a叫做二次函数的系数,b叫做一次项的系数,c叫作常数项。
二次函数:
抛物线:
二次函数的图象都是抛物线。
一般地,形如
(a,b,c是常数,
__)的函数,叫做二次函数.
y=ax2+bx+c
a
≠0
[注意]
(1)等号右边必须是整式;(2)自变量的最高次数是2;(3)当b=0,c=0时,y=ax2是特殊的二次函数.
二次函数的概念
开口方向与
a
的关系;
注意:
抛物线与
y
轴的交点与
c
的关系;
对称轴与
a,b
的关系;
抛物线与
x
轴交点数目与
b2-4ac
的符号关系。
一般地,抛物线
y=ax2
的对称轴是____轴,顶点是_______.
当a
>
0时,抛物线的开口向__,顶点是抛物线的________,a
越大,抛物线的开口越___;当a
<
0时,抛物线的开口向____,顶点是抛物线的最____点,a
越大,抛物线的开口越____.
y
原点
最低点
上
小
下
高
大
抛物线
y=ax2
的图象
:
抛物线
y
=
a
(x-h)2
+k
图象的移动
:
一般地,抛物线
y
=
a
(x-h)2
+k
与
y
=
ax2
形状相同,位置不同,把抛物线
y
=
ax2
向上(下)向左(右)平移,可以得到抛物线
y
=
a
(x-h)2
+k
.平移的方向、距离要根据
h,k
的值来决定.
(1)当a>0时,开口向上;
当a<0时,开口向下;
(2)对称轴是直线
x=h;
(3)顶点坐标是(h,k).
抛物线
y
=
a
(x-h)2
+k
(顶点式)的图象特点:
顶点坐标:
对称轴:
抛物线
y
=
ax?+bx+c
(一般式)
的图象特点:
y
=
ax?+bx+c
一般地,因为抛物线
y
=
ax?+bx+c
的顶点是最低(高)点,所以当
时,二次函数
y
=
ax?+bx+c
有最小(大)值
。
二次函数的最值问题:
二次函数
y=ax2+bx+c
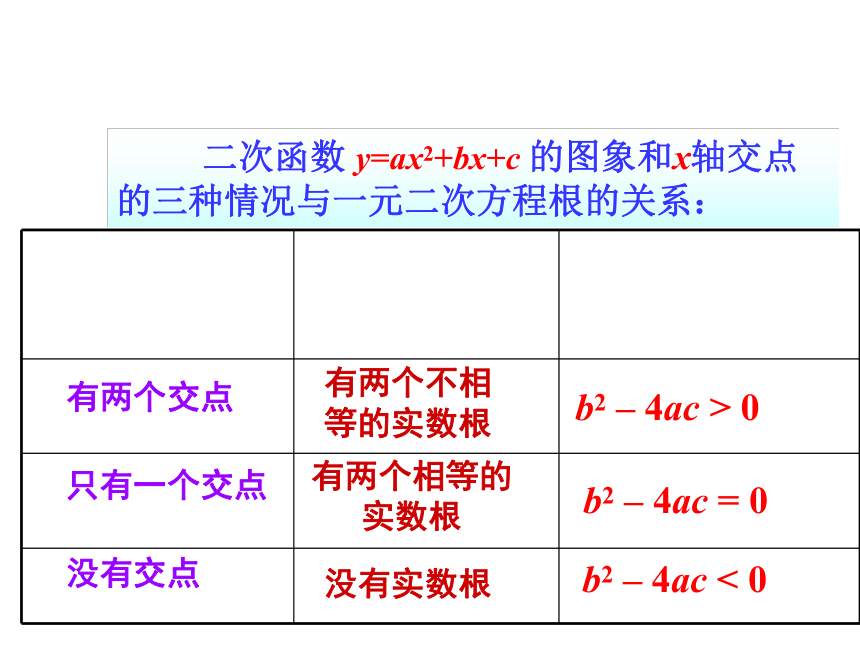
的图象和x轴交点的三种情况与一元二次方程根的关系:
有两个交点
有两个不相等的实数根
只有一个交点
有两个相等的实数根
没有交点
没有实数根
b2
–
4ac
>
0
b2
–
4ac
=
0
b2
–
4ac
<
0
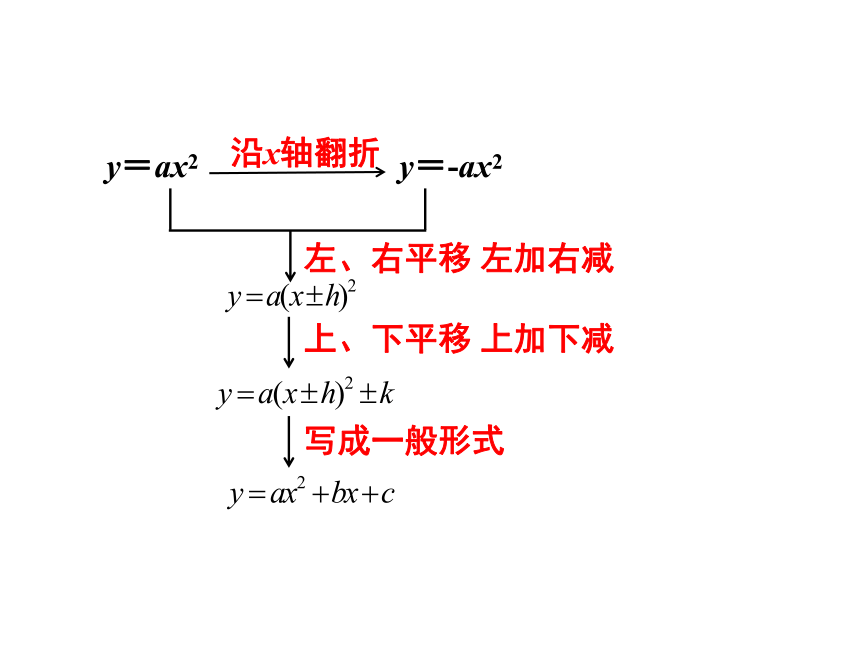
y=ax2
左、右平移
左加右减
上、下平移
上加下减
y=-ax2
写成一般形式
沿x轴翻折
4.二次函数表达式的求法
1.一般式法:y=ax2+bx+c
(a≠
0)
2.顶点法:y=a(x-h)2+k(a≠0)
3.交点法:y=a(x-x1)(x-x2)(a≠0)
1.
二次函数的定义、图象、图象的平移、性质、图象与系数的关系。
2.
二次函数解析式求法。
3.
二次函数图象与一元二次方程的根的关系。
中考热点
1.
二次函数的形式及结构特点。
2.
忽略自变量的取值范围,误认为二次函数的最值点就是顶点。
3.
二次函数与一元二次方程的关系。
4.
点的坐标与距离的区别和联系。
本章易错点
知识运用了,你是最棒的!
加油!
抛物线y=x2-2x+3的顶点坐标为________.
【解析】
方法一:配方,得y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
方法二代入公式
,
,
则顶点坐标为(1,2).
(1,2)
解决此类题目可以
先把二次函数y=ax2+bx+c配方为顶点式y=a(x-h)2+k的形式,得到:对称轴是直线x=h,最值为y=k,顶点坐标为(h,k);
也可以直接利用公式求解.
对于y=2(x-3)2+2的图像下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为y=3
C.当x≥3时,y随x的增大而增大
D.当x≥3时,y随x的增大而减小
C
针对训练
下列函数中,当x>0时,y值随x值增大而减小的是(
)
A.
y=
B.y=x-1
C.
D.y=-3x2
D
二次函数y=-x2+bx+c的图像如图所示,若点A(x1,y1),B(x2,y2)在此函数图像上,且x1A.
y1≤y2
B.y1C.y1≥y2
D.y1>y2
由图像看出,抛物线开口向下,对称轴是x=1,当x<1时,y随x的增大而增大.
∵x1.
故选B.
B
已知二次函数y=ax2+bx+c的图像如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2.
其中正确的个数是( )
A.1 B.2 C.3 D.4
D
将抛物线y=x2-6x+5向上平移
2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6
B.y=(x-4)2-2
C.y=(x-2)2-2
D.y=(x-1)2-3
因为y=x2-6x+5=(x-3)2-4,所以向上平移2个单位长度,再向右平移1个单位长度后,得到的解析式为y=(x-3-1)2-4+2,即y=
(x-4)2-2.故选B.
若抛物线
y=-7(x+4)2-1平移得到
y=-7x2,则可能(
)
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向下平移4个单位
B
已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.
解:设所求的二次函数为y=ax2+bx+c,
由题意得:
解得,
a=2,b=-3,c=5.
∴
所求的二次函数为y=2x2-3x+5.
已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的表达式.
解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状
相同?
a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
?
顶点为(1,5)或(1,-5)
所以其表达式为:
(1)
y=(x-1)2+5
(2)
y=(x-1)2-5
(3)
y=-(x-1)2+5
(4)
y=-(x-1)2-5
若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A.x1=0,x2=6
B.x1=1,x2=7
C.x1=1,x2=﹣7
D.x1=﹣1,x2=7
∵二次函数y=x2+mx的对称轴是x=3,
∴
=3,解得m=-6,
∴关于x的方程x2+mx=7可化为x2-6x-7=0,
即(x+1)(x-7)=0,解得x1=-1,x2=7.
故选D.
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
解:(1)根据题意,得
解得k=-1,b=120.故所求一次函数的表达式为y=-x+120.
(2)W=(x-60)?(-x+120)=-x2+180x-7200=-(x-90)2+900,
∵抛物线的开口向下,
∴当x<90时,W随x的增大而增大,
而60≤x≤60×(1+45%),即60≤x≤87,
∴当x=87时,W有最大值,此时W=-(87-90)2+900=891.
一家电脑公司推出一款新型电脑,投放市场以来3个月的利润情况如图所示,该图可以近似看作为抛物线的一部分,请结合图象,解答以下问题:
(1)求该抛物线对应的二次函数解析式;(2)该公司在经营此款电脑过程中,第几月的利润最大?最大利润是多少?
(3)若照此经营下去,请你结合所学的知识,对公司在此款电脑的经营状况(是否亏损?何时亏损?)作预测分析.
解:(1)因图象过原点,则设函数解析式为y=ax2+bx,由图象的点的含义,得
解得a=-1,b=14.
故所求一次函数的表达式为y=-x2+14x.
(2)
y=-x2+14x=-(x-7)2+49.即当x=7时,利润最大,y=49(万元)
(3)
没有利润,即y=-x2+14x=0.解得x1=0(舍去)或x2=14,而这时利润为滑坡状态,所以第15个月,公司亏损.
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长;
(2)设四边形DEBG的面积为S,求S与x的函数关系式;
(3)当x为何值时,S有最大值?并求出这个最大值.
解:(1)由题意,得EF=AE=DE=BC=x,AB=30.
∴BF=2x-30.
(2)∵∠F=∠A=45°,∠CBF-=∠ABC=90°,
∴∠BGF=∠F=45°,BG=BF=2x-30.
所以S△DEF-S△GBF=
DE2-
BF2=
x2-
(2x-30)2=
x2+60x-450.
(3)S=
x2+60x-450=
(x-20)2+150.
∵a=
<0,15<20<30,
∴当x=20时,S有最大值,
最大值为150.
张大伯准备用40m长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25m的墙,设计了如图一个矩形的羊圈.
(1)请你求出张大伯矩形羊圈的面积;
(2)请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由.
25m
解:(1)由题意得羊圈的长为25m,宽为(40-25)÷2=7.5(m).
故羊圈的面积为25×7.5=187.5(m2)
(2)设羊圈与墙垂直的一边为xm,则与墙相对的一边长为(40-2x)m,羊圈的面积S=x(40-2x)=-2x2+40x=-2(x-10)2+200,(0<x<20).
因为0<10<20,所以当x=10时,S有最大值,此时S=200.
故张大伯的设计不合理.羊圈与墙垂直的两边长为10m,而与墙相对的一边长为(40-2x)m=20m.
成功不是靠梦想和希望,而是靠努力和实践。
加油吧!同学们!
二次函数的总结与复习
学习目标
复习二次函数的相关知识点
提高用二次函数的相关知识点解决问题的能力
形如
(a、b、c是常数,a≠0)的函数叫做
x
的二次函数,a叫做二次函数的系数,b叫做一次项的系数,c叫作常数项。
二次函数:
抛物线:
二次函数的图象都是抛物线。
一般地,形如
(a,b,c是常数,
__)的函数,叫做二次函数.
y=ax2+bx+c
a
≠0
[注意]
(1)等号右边必须是整式;(2)自变量的最高次数是2;(3)当b=0,c=0时,y=ax2是特殊的二次函数.
二次函数的概念
开口方向与
a
的关系;
注意:
抛物线与
y
轴的交点与
c
的关系;
对称轴与
a,b
的关系;
抛物线与
x
轴交点数目与
b2-4ac
的符号关系。
一般地,抛物线
y=ax2
的对称轴是____轴,顶点是_______.
当a
>
0时,抛物线的开口向__,顶点是抛物线的________,a
越大,抛物线的开口越___;当a
<
0时,抛物线的开口向____,顶点是抛物线的最____点,a
越大,抛物线的开口越____.
y
原点
最低点
上
小
下
高
大
抛物线
y=ax2
的图象
:
抛物线
y
=
a
(x-h)2
+k
图象的移动
:
一般地,抛物线
y
=
a
(x-h)2
+k
与
y
=
ax2
形状相同,位置不同,把抛物线
y
=
ax2
向上(下)向左(右)平移,可以得到抛物线
y
=
a
(x-h)2
+k
.平移的方向、距离要根据
h,k
的值来决定.
(1)当a>0时,开口向上;
当a<0时,开口向下;
(2)对称轴是直线
x=h;
(3)顶点坐标是(h,k).
抛物线
y
=
a
(x-h)2
+k
(顶点式)的图象特点:
顶点坐标:
对称轴:
抛物线
y
=
ax?+bx+c
(一般式)
的图象特点:
y
=
ax?+bx+c
一般地,因为抛物线
y
=
ax?+bx+c
的顶点是最低(高)点,所以当
时,二次函数
y
=
ax?+bx+c
有最小(大)值
。
二次函数的最值问题:
二次函数
y=ax2+bx+c
的图象和x轴交点的三种情况与一元二次方程根的关系:
有两个交点
有两个不相等的实数根
只有一个交点
有两个相等的实数根
没有交点
没有实数根
b2
–
4ac
>
0
b2
–
4ac
=
0
b2
–
4ac
<
0
y=ax2
左、右平移
左加右减
上、下平移
上加下减
y=-ax2
写成一般形式
沿x轴翻折
4.二次函数表达式的求法
1.一般式法:y=ax2+bx+c
(a≠
0)
2.顶点法:y=a(x-h)2+k(a≠0)
3.交点法:y=a(x-x1)(x-x2)(a≠0)
1.
二次函数的定义、图象、图象的平移、性质、图象与系数的关系。
2.
二次函数解析式求法。
3.
二次函数图象与一元二次方程的根的关系。
中考热点
1.
二次函数的形式及结构特点。
2.
忽略自变量的取值范围,误认为二次函数的最值点就是顶点。
3.
二次函数与一元二次方程的关系。
4.
点的坐标与距离的区别和联系。
本章易错点
知识运用了,你是最棒的!
加油!
抛物线y=x2-2x+3的顶点坐标为________.
【解析】
方法一:配方,得y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
方法二代入公式
,
,
则顶点坐标为(1,2).
(1,2)
解决此类题目可以
先把二次函数y=ax2+bx+c配方为顶点式y=a(x-h)2+k的形式,得到:对称轴是直线x=h,最值为y=k,顶点坐标为(h,k);
也可以直接利用公式求解.
对于y=2(x-3)2+2的图像下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为y=3
C.当x≥3时,y随x的增大而增大
D.当x≥3时,y随x的增大而减小
C
针对训练
下列函数中,当x>0时,y值随x值增大而减小的是(
)
A.
y=
B.y=x-1
C.
D.y=-3x2
D
二次函数y=-x2+bx+c的图像如图所示,若点A(x1,y1),B(x2,y2)在此函数图像上,且x1
y1≤y2
B.y1
D.y1>y2
由图像看出,抛物线开口向下,对称轴是x=1,当x<1时,y随x的增大而增大.
∵x1
故选B.
B
已知二次函数y=ax2+bx+c的图像如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2.
其中正确的个数是( )
A.1 B.2 C.3 D.4
D
将抛物线y=x2-6x+5向上平移
2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6
B.y=(x-4)2-2
C.y=(x-2)2-2
D.y=(x-1)2-3
因为y=x2-6x+5=(x-3)2-4,所以向上平移2个单位长度,再向右平移1个单位长度后,得到的解析式为y=(x-3-1)2-4+2,即y=
(x-4)2-2.故选B.
若抛物线
y=-7(x+4)2-1平移得到
y=-7x2,则可能(
)
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向下平移4个单位
B
已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.
解:设所求的二次函数为y=ax2+bx+c,
由题意得:
解得,
a=2,b=-3,c=5.
∴
所求的二次函数为y=2x2-3x+5.
已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的表达式.
解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状
相同?
a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
?
顶点为(1,5)或(1,-5)
所以其表达式为:
(1)
y=(x-1)2+5
(2)
y=(x-1)2-5
(3)
y=-(x-1)2+5
(4)
y=-(x-1)2-5
若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A.x1=0,x2=6
B.x1=1,x2=7
C.x1=1,x2=﹣7
D.x1=﹣1,x2=7
∵二次函数y=x2+mx的对称轴是x=3,
∴
=3,解得m=-6,
∴关于x的方程x2+mx=7可化为x2-6x-7=0,
即(x+1)(x-7)=0,解得x1=-1,x2=7.
故选D.
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
解:(1)根据题意,得
解得k=-1,b=120.故所求一次函数的表达式为y=-x+120.
(2)W=(x-60)?(-x+120)=-x2+180x-7200=-(x-90)2+900,
∵抛物线的开口向下,
∴当x<90时,W随x的增大而增大,
而60≤x≤60×(1+45%),即60≤x≤87,
∴当x=87时,W有最大值,此时W=-(87-90)2+900=891.
一家电脑公司推出一款新型电脑,投放市场以来3个月的利润情况如图所示,该图可以近似看作为抛物线的一部分,请结合图象,解答以下问题:
(1)求该抛物线对应的二次函数解析式;(2)该公司在经营此款电脑过程中,第几月的利润最大?最大利润是多少?
(3)若照此经营下去,请你结合所学的知识,对公司在此款电脑的经营状况(是否亏损?何时亏损?)作预测分析.
解:(1)因图象过原点,则设函数解析式为y=ax2+bx,由图象的点的含义,得
解得a=-1,b=14.
故所求一次函数的表达式为y=-x2+14x.
(2)
y=-x2+14x=-(x-7)2+49.即当x=7时,利润最大,y=49(万元)
(3)
没有利润,即y=-x2+14x=0.解得x1=0(舍去)或x2=14,而这时利润为滑坡状态,所以第15个月,公司亏损.
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长;
(2)设四边形DEBG的面积为S,求S与x的函数关系式;
(3)当x为何值时,S有最大值?并求出这个最大值.
解:(1)由题意,得EF=AE=DE=BC=x,AB=30.
∴BF=2x-30.
(2)∵∠F=∠A=45°,∠CBF-=∠ABC=90°,
∴∠BGF=∠F=45°,BG=BF=2x-30.
所以S△DEF-S△GBF=
DE2-
BF2=
x2-
(2x-30)2=
x2+60x-450.
(3)S=
x2+60x-450=
(x-20)2+150.
∵a=
<0,15<20<30,
∴当x=20时,S有最大值,
最大值为150.
张大伯准备用40m长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25m的墙,设计了如图一个矩形的羊圈.
(1)请你求出张大伯矩形羊圈的面积;
(2)请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由.
25m
解:(1)由题意得羊圈的长为25m,宽为(40-25)÷2=7.5(m).
故羊圈的面积为25×7.5=187.5(m2)
(2)设羊圈与墙垂直的一边为xm,则与墙相对的一边长为(40-2x)m,羊圈的面积S=x(40-2x)=-2x2+40x=-2(x-10)2+200,(0<x<20).
因为0<10<20,所以当x=10时,S有最大值,此时S=200.
故张大伯的设计不合理.羊圈与墙垂直的两边长为10m,而与墙相对的一边长为(40-2x)m=20m.
成功不是靠梦想和希望,而是靠努力和实践。
加油吧!同学们!
同课章节目录
