人教版数学八年级上册11.2.1-三角形的内角-教案设计
文档属性
| 名称 | 人教版数学八年级上册11.2.1-三角形的内角-教案设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 529.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览


文档简介
三角形的内角
【教学目标】
1.探索并证明三角形内角和定理,能应用三角形内角和定理解决一些简单的实际问题。
2.理解三角形内角和的探索,其本质就是想办法把三个内角拼在同一处,使得它们构成一个平角,借助于拼合的方法来引出作平行线的方法。
3.通过测量、剪拼、猜想、推理等数学活动,探索三角形的内角和,会多角度寻求解决问题的途径,发现操作实验的局限性,感受推理证明的必要性,发展合情推理能力和语言表达能力。
【教学重难点】
1.探索并证明三角形内角和定理,体会证明的必要性。
2.如何添加辅助线证明三角形内角和定理。
【教学过程】
一、创设情境,引入新课。
问题1:动画中三个兄弟都是什么图形?(三角形)
它们分别叫什么名字。(锐角三角形、直角三角形、钝角三角形)
问题2:它们按什么进行分类?(按内角的大小来分为锐角三角形、直角三角形、钝角三角形)
问题3:它们在争吵什么?(内角和)
什么是内角和?你们怎么理解?(内角和就是三个内角的和)
问题4:你认为谁的内角和最大?为什么?(一样大,因为三角形的内角和都是180度)
今天我们进一步来研究三角形的三个内角,看看它们的内角和为什么是180°。(书课题)
设计意图:问题是思维的出发点,教师从学生实际出发,为学生创设丰富的问题情境,自然引入新课,激发了学生学习兴趣和求知欲望。
二、探索并证明三角形内角和定理。
教师:在小学时,同学们就学过三角形的内角和为180°,那是不是所有的三角形的内角和都是180°呢?你们还记得这个结论是用什么方法得到的吗?
学生活动:学生思考后举手回答。
教师活动:下面老师把我们小学研究过的方法做成一个微视频,我们大家一起来回顾一下。大家观看的时候一定要想想哪种方法更能准确的得到三角形的内角和为180°呢?
师生活动:通过回顾同学们小学研究过的度量、剪拼或折拼的方法验证三角形三个内角和等于180°,但同学们明确地感受到了这些方法的弊端,度量法存在误差现象,几何画板度量的结论只适用于所有三角形中有限的几个,而形状不同的三角形有无数多个,画板是不能逐一验证的,而剪拼和折拼法明显不能保证拼后的一定是平角,只是感官上看上去是平角而已,这些方法都没有说服力。那么在中学,我们将如何来说明“所有的三角形的三个内角的和都等于180°”这个结论呢?
师生活动:小组交流,小组代表汇报交流结果,最后达成共识:需要通过推理的方法去证明。
设计意图:因为是学生小学操作过的实验,所以教学时采用了微视频播放帮助学生回忆,目的一是避免课堂无必要的浪费时间,二是让学生通过观察实验操作,一方面发现实验操作的局限性(视觉误差、度量误差,实验有限性与三角形个数无限的矛盾),进而了解证明的必要性;另一方面从实验的过程中受到启发,为下一步证明三角形内角和定理提供思路和方法。
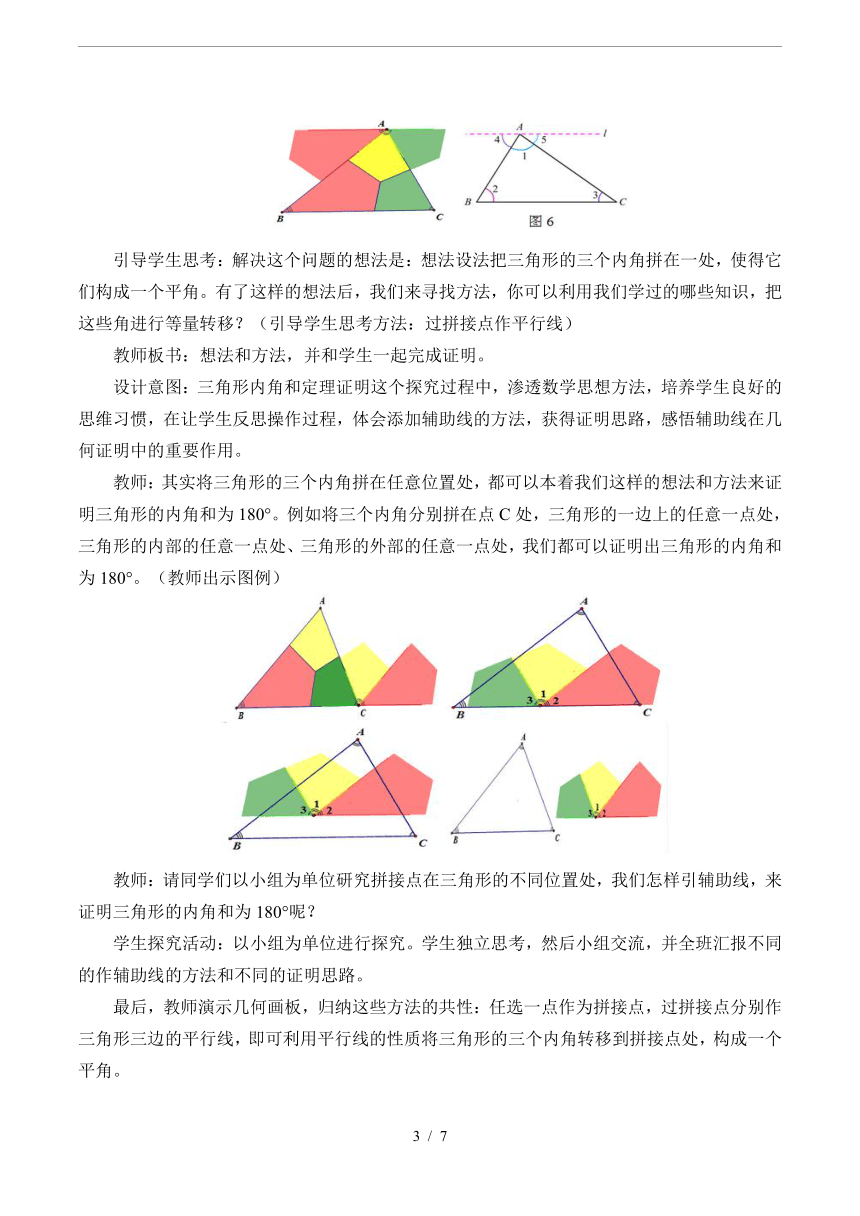
教师:虽然剪拼和折拼的方法都有很大的弊端,但是这些方法给了我们证明的思路。我们以剪拼为例,哪位同学能到前面来帮助老师把三角形的三个角拼在顶点A处。你能从以上的操作过程中受到启发,想出证明“三角形内角和等于180°”的方法吗?
引导学生思考:解决这个问题的想法是:想法设法把三角形的三个内角拼在一处,使得它们构成一个平角。有了这样的想法后,我们来寻找方法,你可以利用我们学过的哪些知识,把这些角进行等量转移?(引导学生思考方法:过拼接点作平行线)
教师板书:想法和方法,并和学生一起完成证明。
设计意图:三角形内角和定理证明这个探究过程中,渗透数学思想方法,培养学生良好的思维习惯,在让学生反思操作过程,体会添加辅助线的方法,获得证明思路,感悟辅助线在几何证明中的重要作用。
教师:其实将三角形的三个内角拼在任意位置处,都可以本着我们这样的想法和方法来证明三角形的内角和为180°。例如将三个内角分别拼在点C处,三角形的一边上的任意一点处,三角形的内部的任意一点处、三角形的外部的任意一点处,我们都可以证明出三角形的内角和为180°。(教师出示图例)
教师:请同学们以小组为单位研究拼接点在三角形的不同位置处,我们怎样引辅助线,来证明三角形的内角和为180°呢?
学生探究活动:以小组为单位进行探究。学生独立思考,然后小组交流,并全班汇报不同的作辅助线的方法和不同的证明思路。
最后,教师演示几何画板,归纳这些方法的共性:任选一点作为拼接点,过拼接点分别作三角形三边的平行线,即可利用平行线的性质将三角形的三个内角转移到拼接点处,构成一个平角。
设计意图:鼓励学生从不同的角度思考问题,进一步体会作辅助线的方法,丰富学生的解题经验。此处可根据学生的实际情况进行取舍。
三、运用三角形内角和定理。
例1:如图11,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线。求∠ADB的度数。
师生活动:
1.教师引导学生分析解题思路:要想求出∠ADB的度数,根据三角形内角和定理,只要求出∠DAB的度数即可。由于∠BAC=40°,AD是△ABC的角平分线,所以很容易得出∠DAB=20°。
2.学生独立完成解题过程,一名学生板书。
3.师生共同分析学生板书的解题过程。
设计意图:运用三角形内角和定理求相关角的度数,使学生进一步巩固定理内容。
例2:如图12,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB呢?
师生活动:
1.教师引导学生将实际问题转化为数学中的三角形的角的问题,即A,B,C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角。
2.教师引导学生分析解题思路:在△ABC中,若能求出∠CAB和∠ABC,根据三角形内角和定理,即可求出∠ACB,而根据已知条件,∠CAB和∠ABC很容易求出。
3.学生独立完成解题过程,并相互批改。
设计意图:利用三角形内角和定理解决生活中的简单问题,提高学生的应用意识和数学表达能力。
四、互余定理。
如图,在直角三角形ABC中,∠C=90°,由三角形内角和定理,得
∠A+∠B+∠C=180°,即∠A+∠B+90°=180°,所以∠A+∠B=90°
我们以此可以看出,三角形内角和定理在直角三角形中也是适用的,成立。
从上面我们可以得出:∠A+∠B的和是多少?
生:90度。
师:对,这两个角的和恰好等于∠C的大小,这不是一种巧合,这是直角三角形的一个性质。
我们得出:在直角三角形中,如果两个锐角的和等于90°,那么我们说这两个锐角是互余的。
正在这里,我们有一种专门的标记直角三角形的特殊符号:“Rt”
直角三角形ABC可以写成Rt△ABC。
大家在演草纸上试着书写下这个符号,一定要分清,第一个字母是大写,第二个字母是小写哦!大家明白了吗?
生:明白了!
师:那好,下面我们就看下这个性质的应用,我们看例3。
例3:如图,∠C=∠D=90°,AD,BC相交于点E,∠CAE于∠DBC有什么关系?为什么?
解:在Rt△ACE中,∠CAE=90°-∠AEC.
在Rt△BDE中,∠DBE=90°-∠BED.
因为∠AEC=∠BED,
所以∠CAE=∠DBE.
好,我们完成了这个性质的应用。我们进一步思考:
如果一个三角形是直角三角形,那么这个三角形有两个角互余。反过来,有两个角互余的三角形是直角三角形吗?大家思考一下,举手回答。
生:是,有两个角互余,说这两个角的和是90°,再根据三角形内角和等于180°,可以得到另外的一个角是90°,即是直角,进而可以判断这个三角形是直角三角形。
师:回答的非常好,思路清晰,严密。
五、练习。
1.如图,说出各图中∠1的度数。
2.如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。从C处观测A,B两处时视角∠ACB是多少?
师生活动:学生回答第1题,独立完成第2题。
设计意图:第1题是通过简单的计算,使学生进一步熟悉三角形内角和定理。
第2题是让学生运用三角形内角和定理解决简单的实际问题。
六、小结。
教师与学生一起回顾本节课所学的主要内容,并请学生回答以下问题:
1.本节课学习了哪些主要内容?
2.为什么要用推理的方法证明“三角形的内角和等于180°”?
3.你是怎么找到三角形内角和定理的证明思路的?
4.在探究三角形的内角和的过程中,你感受到了哪些研究问题的思想方法?
设计意图:通过小结,使学生梳理本节课所学内容,掌握本节课的核心——三角形内角和定理,进一步体会证明的必要性,感悟辅助线的添加方法在几何证明中的作用,体会数学研究学习中的思想方法的重要性。
七、目标测试。
1.如图,写出下列图中x的值。
设计意图:考查学生对三角形内角和定理的理解。
2.如图,某模具厂的一种模具按规定BA,CD的延长线的夹角应为61°,因交点不在模板上,不方便测量,王师傅测得∠B=42°,∠C=79°,请你帮王师傅判断该模具是否符合要求,并说明理由。
设计意图:考查学生运用三角形内角和定理解决实际问题。
3.如图,在△ABC中,∠B=45°,∠C=75°,AD是△ABC的角平分线。求∠ADC的度数。
设计意图:考查学生运用三角形内角和定理及角平分线的定义解决几何问题。
/
【教学目标】
1.探索并证明三角形内角和定理,能应用三角形内角和定理解决一些简单的实际问题。
2.理解三角形内角和的探索,其本质就是想办法把三个内角拼在同一处,使得它们构成一个平角,借助于拼合的方法来引出作平行线的方法。
3.通过测量、剪拼、猜想、推理等数学活动,探索三角形的内角和,会多角度寻求解决问题的途径,发现操作实验的局限性,感受推理证明的必要性,发展合情推理能力和语言表达能力。
【教学重难点】
1.探索并证明三角形内角和定理,体会证明的必要性。
2.如何添加辅助线证明三角形内角和定理。
【教学过程】
一、创设情境,引入新课。
问题1:动画中三个兄弟都是什么图形?(三角形)
它们分别叫什么名字。(锐角三角形、直角三角形、钝角三角形)
问题2:它们按什么进行分类?(按内角的大小来分为锐角三角形、直角三角形、钝角三角形)
问题3:它们在争吵什么?(内角和)
什么是内角和?你们怎么理解?(内角和就是三个内角的和)
问题4:你认为谁的内角和最大?为什么?(一样大,因为三角形的内角和都是180度)
今天我们进一步来研究三角形的三个内角,看看它们的内角和为什么是180°。(书课题)
设计意图:问题是思维的出发点,教师从学生实际出发,为学生创设丰富的问题情境,自然引入新课,激发了学生学习兴趣和求知欲望。
二、探索并证明三角形内角和定理。
教师:在小学时,同学们就学过三角形的内角和为180°,那是不是所有的三角形的内角和都是180°呢?你们还记得这个结论是用什么方法得到的吗?
学生活动:学生思考后举手回答。
教师活动:下面老师把我们小学研究过的方法做成一个微视频,我们大家一起来回顾一下。大家观看的时候一定要想想哪种方法更能准确的得到三角形的内角和为180°呢?
师生活动:通过回顾同学们小学研究过的度量、剪拼或折拼的方法验证三角形三个内角和等于180°,但同学们明确地感受到了这些方法的弊端,度量法存在误差现象,几何画板度量的结论只适用于所有三角形中有限的几个,而形状不同的三角形有无数多个,画板是不能逐一验证的,而剪拼和折拼法明显不能保证拼后的一定是平角,只是感官上看上去是平角而已,这些方法都没有说服力。那么在中学,我们将如何来说明“所有的三角形的三个内角的和都等于180°”这个结论呢?
师生活动:小组交流,小组代表汇报交流结果,最后达成共识:需要通过推理的方法去证明。
设计意图:因为是学生小学操作过的实验,所以教学时采用了微视频播放帮助学生回忆,目的一是避免课堂无必要的浪费时间,二是让学生通过观察实验操作,一方面发现实验操作的局限性(视觉误差、度量误差,实验有限性与三角形个数无限的矛盾),进而了解证明的必要性;另一方面从实验的过程中受到启发,为下一步证明三角形内角和定理提供思路和方法。
教师:虽然剪拼和折拼的方法都有很大的弊端,但是这些方法给了我们证明的思路。我们以剪拼为例,哪位同学能到前面来帮助老师把三角形的三个角拼在顶点A处。你能从以上的操作过程中受到启发,想出证明“三角形内角和等于180°”的方法吗?
引导学生思考:解决这个问题的想法是:想法设法把三角形的三个内角拼在一处,使得它们构成一个平角。有了这样的想法后,我们来寻找方法,你可以利用我们学过的哪些知识,把这些角进行等量转移?(引导学生思考方法:过拼接点作平行线)
教师板书:想法和方法,并和学生一起完成证明。
设计意图:三角形内角和定理证明这个探究过程中,渗透数学思想方法,培养学生良好的思维习惯,在让学生反思操作过程,体会添加辅助线的方法,获得证明思路,感悟辅助线在几何证明中的重要作用。
教师:其实将三角形的三个内角拼在任意位置处,都可以本着我们这样的想法和方法来证明三角形的内角和为180°。例如将三个内角分别拼在点C处,三角形的一边上的任意一点处,三角形的内部的任意一点处、三角形的外部的任意一点处,我们都可以证明出三角形的内角和为180°。(教师出示图例)
教师:请同学们以小组为单位研究拼接点在三角形的不同位置处,我们怎样引辅助线,来证明三角形的内角和为180°呢?
学生探究活动:以小组为单位进行探究。学生独立思考,然后小组交流,并全班汇报不同的作辅助线的方法和不同的证明思路。
最后,教师演示几何画板,归纳这些方法的共性:任选一点作为拼接点,过拼接点分别作三角形三边的平行线,即可利用平行线的性质将三角形的三个内角转移到拼接点处,构成一个平角。
设计意图:鼓励学生从不同的角度思考问题,进一步体会作辅助线的方法,丰富学生的解题经验。此处可根据学生的实际情况进行取舍。
三、运用三角形内角和定理。
例1:如图11,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线。求∠ADB的度数。
师生活动:
1.教师引导学生分析解题思路:要想求出∠ADB的度数,根据三角形内角和定理,只要求出∠DAB的度数即可。由于∠BAC=40°,AD是△ABC的角平分线,所以很容易得出∠DAB=20°。
2.学生独立完成解题过程,一名学生板书。
3.师生共同分析学生板书的解题过程。
设计意图:运用三角形内角和定理求相关角的度数,使学生进一步巩固定理内容。
例2:如图12,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB呢?
师生活动:
1.教师引导学生将实际问题转化为数学中的三角形的角的问题,即A,B,C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角。
2.教师引导学生分析解题思路:在△ABC中,若能求出∠CAB和∠ABC,根据三角形内角和定理,即可求出∠ACB,而根据已知条件,∠CAB和∠ABC很容易求出。
3.学生独立完成解题过程,并相互批改。
设计意图:利用三角形内角和定理解决生活中的简单问题,提高学生的应用意识和数学表达能力。
四、互余定理。
如图,在直角三角形ABC中,∠C=90°,由三角形内角和定理,得
∠A+∠B+∠C=180°,即∠A+∠B+90°=180°,所以∠A+∠B=90°
我们以此可以看出,三角形内角和定理在直角三角形中也是适用的,成立。
从上面我们可以得出:∠A+∠B的和是多少?
生:90度。
师:对,这两个角的和恰好等于∠C的大小,这不是一种巧合,这是直角三角形的一个性质。
我们得出:在直角三角形中,如果两个锐角的和等于90°,那么我们说这两个锐角是互余的。
正在这里,我们有一种专门的标记直角三角形的特殊符号:“Rt”
直角三角形ABC可以写成Rt△ABC。
大家在演草纸上试着书写下这个符号,一定要分清,第一个字母是大写,第二个字母是小写哦!大家明白了吗?
生:明白了!
师:那好,下面我们就看下这个性质的应用,我们看例3。
例3:如图,∠C=∠D=90°,AD,BC相交于点E,∠CAE于∠DBC有什么关系?为什么?
解:在Rt△ACE中,∠CAE=90°-∠AEC.
在Rt△BDE中,∠DBE=90°-∠BED.
因为∠AEC=∠BED,
所以∠CAE=∠DBE.
好,我们完成了这个性质的应用。我们进一步思考:
如果一个三角形是直角三角形,那么这个三角形有两个角互余。反过来,有两个角互余的三角形是直角三角形吗?大家思考一下,举手回答。
生:是,有两个角互余,说这两个角的和是90°,再根据三角形内角和等于180°,可以得到另外的一个角是90°,即是直角,进而可以判断这个三角形是直角三角形。
师:回答的非常好,思路清晰,严密。
五、练习。
1.如图,说出各图中∠1的度数。
2.如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。从C处观测A,B两处时视角∠ACB是多少?
师生活动:学生回答第1题,独立完成第2题。
设计意图:第1题是通过简单的计算,使学生进一步熟悉三角形内角和定理。
第2题是让学生运用三角形内角和定理解决简单的实际问题。
六、小结。
教师与学生一起回顾本节课所学的主要内容,并请学生回答以下问题:
1.本节课学习了哪些主要内容?
2.为什么要用推理的方法证明“三角形的内角和等于180°”?
3.你是怎么找到三角形内角和定理的证明思路的?
4.在探究三角形的内角和的过程中,你感受到了哪些研究问题的思想方法?
设计意图:通过小结,使学生梳理本节课所学内容,掌握本节课的核心——三角形内角和定理,进一步体会证明的必要性,感悟辅助线的添加方法在几何证明中的作用,体会数学研究学习中的思想方法的重要性。
七、目标测试。
1.如图,写出下列图中x的值。
设计意图:考查学生对三角形内角和定理的理解。
2.如图,某模具厂的一种模具按规定BA,CD的延长线的夹角应为61°,因交点不在模板上,不方便测量,王师傅测得∠B=42°,∠C=79°,请你帮王师傅判断该模具是否符合要求,并说明理由。
设计意图:考查学生运用三角形内角和定理解决实际问题。
3.如图,在△ABC中,∠B=45°,∠C=75°,AD是△ABC的角平分线。求∠ADC的度数。
设计意图:考查学生运用三角形内角和定理及角平分线的定义解决几何问题。
/
