人教版八年级上册数学课件:13.3.1等腰三角形的性质(27张PPT)
文档属性
| 名称 | 人教版八年级上册数学课件:13.3.1等腰三角形的性质(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 817.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览




文档简介
等腰三角形的性质
学习目标
1、了解等腰三角形的概念, 掌握等腰三角形的性质
2、会运用等腰三角形的概念及性质解决相关问题。
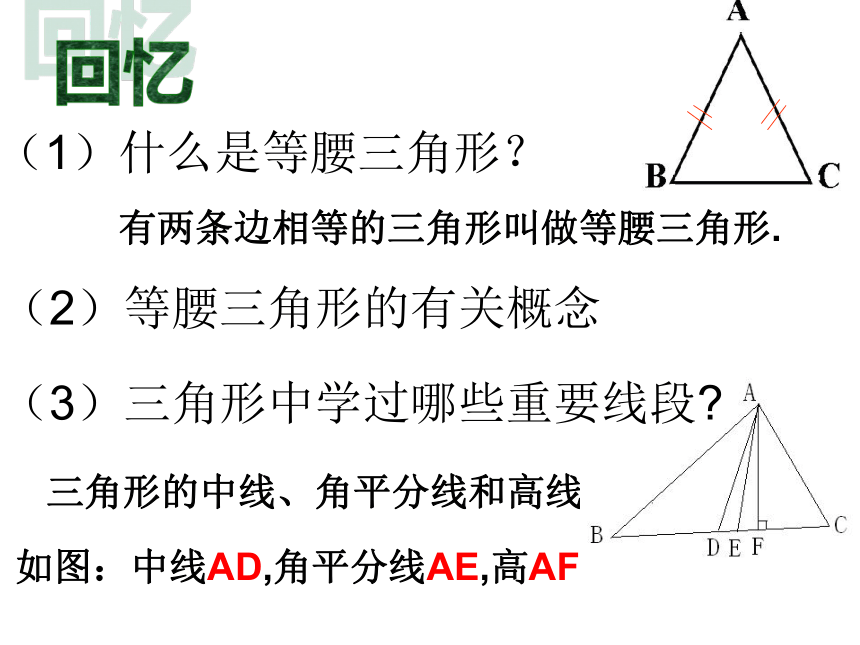
有两条边相等的三角形叫做等腰三角形.
回忆
三角形的中线、角平分线和高线
如图:中线AD,角平分线AE,高AF
(1)什么是等腰三角形?
(2)等腰三角形的有关概念
(3)三角形中学过哪些重要线段?
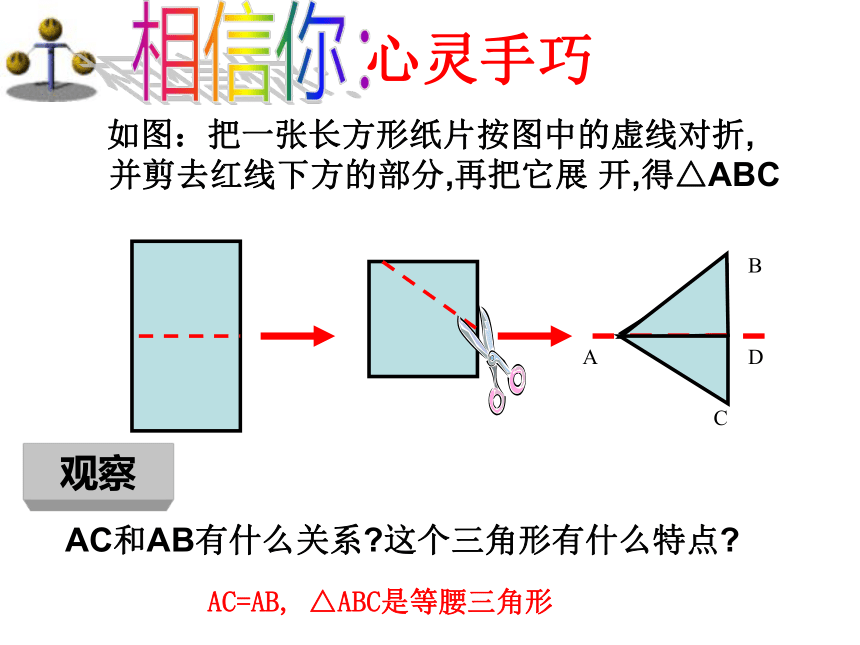
如图:把一张长方形纸片按图中的虚线对折,
并剪去红线下方的部分,再把它展 开,得△ABC
A
C
D
B
观察
AC和AB有什么关系?这个三角形有什么特点?
AC=AB, △ABC是等腰三角形
心灵手巧
相信你:
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
找一找
等腰三角形是轴对称图形吗?
思考
是
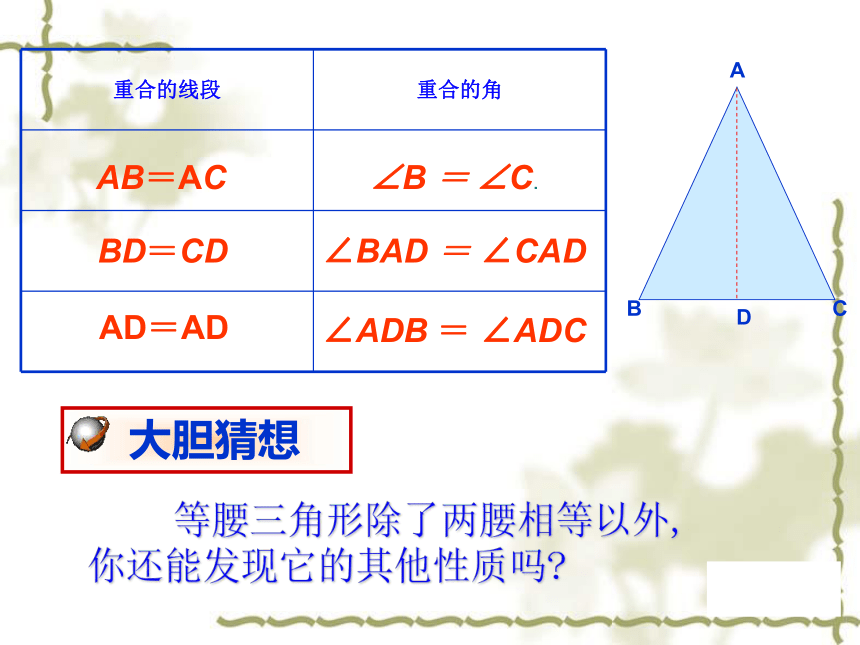
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗?
大胆猜想
猜想与论证
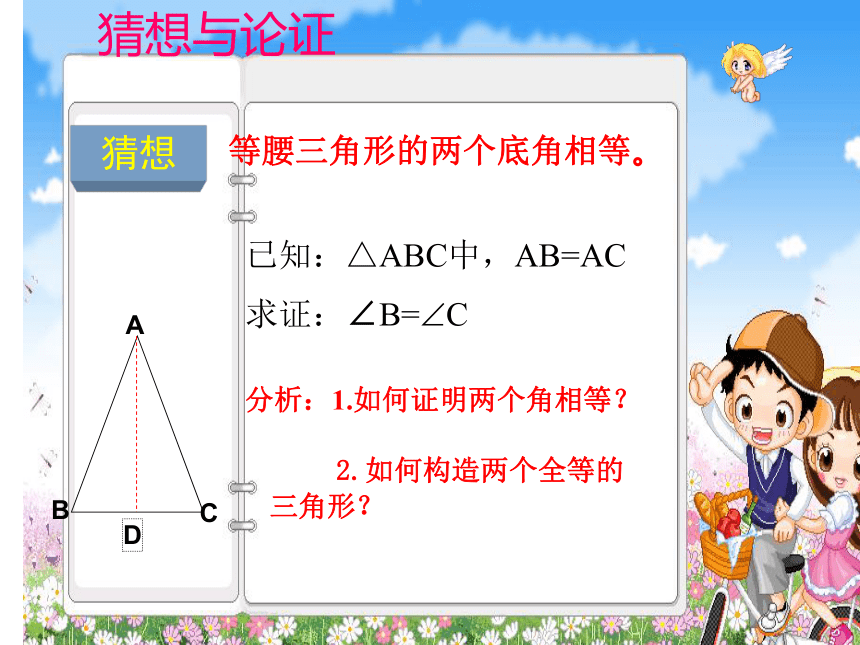
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的 三角形?
猜想
A
B
C
D
A
B
C
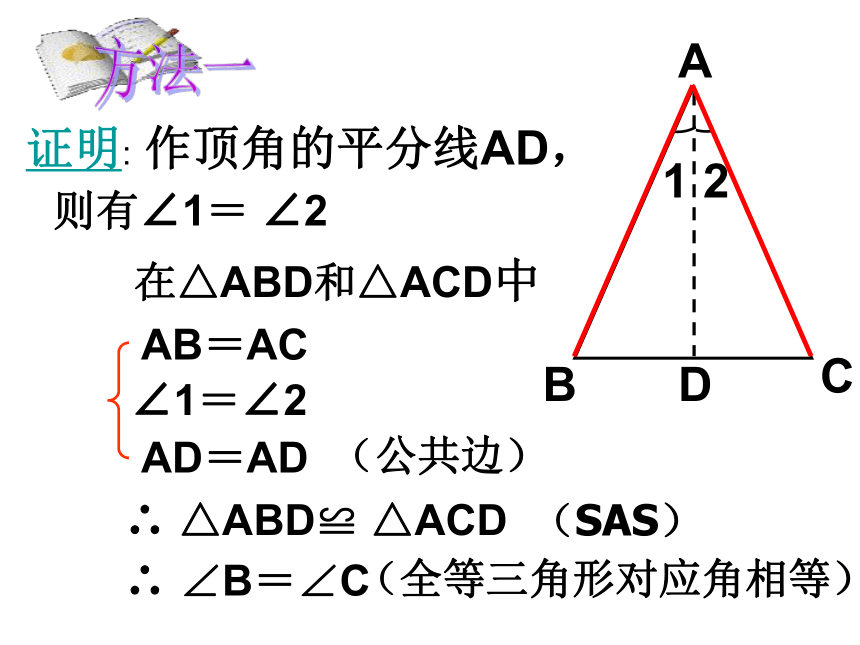
则有∠1= ∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
A
B
C
则有 BD= CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法二
A
B
C
则有 ∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
方法三
归纳结论
等腰三角形的两个底角相等。
性质1
(等边对等角)
用符号语言表示为:
在△ABC中,
∵ AC=AB(已知)
∴ ∠B=∠C (等边对等角)
A
B
C
看谁算得快
如图,在下列等腰三角形中,分别求
出它们的底角的度数。
A
B
C
120°
A
B
C
36°
⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。
75°, 30°
70°,40°或55°,55°
35°,35°
巩固练习(1)
想一想:
刚才的证明除了能得到∠B=∠C 你还能发现什么?
重合的线段
重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
猜想:等腰三角形的顶角平分线,
底边上的中线,底边上的高互相重合
A
B
C
则有∠1= ∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ BD=CD
∠ADB =∠ADC=
90°
论证猜想
(等腰三角形三线合一)
等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合
性质2:
归纳结论
用符号语言表示为:
在△ABC中,AB =AC, 点 D在BC上
1、∵AD ⊥ BC
∴∠ = ∠ , = 。
2、∵AD是中线,
∴ ⊥ ,∠ =∠ 。
3、∵AD是角平分线,
∴ ⊥ , = 。
A
B
C
D
⌒
⌒
1
2
1
2
1
2
BD
CD
AD
BC
1
2
AD
BC
BD
CD
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合!
三线合一
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
为什么不一样?
深入分析
例1、如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数。
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD (等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,∠ABC=∠C=72°
x
⌒
2x
⌒
2x
⌒
⌒
2x
1、等腰三角形的顶角一定是锐角。
2、等腰三角形的底角可能是锐角或者直角、
钝角都可以。
3、等腰三角形的顶角平分线一定垂直底边。
4、等腰三角形的角平分线、中线和高互相重
合。
5、等腰三角形底边上的中线一定平分顶角
(X)
(X)
(√)
(X)
(√)
一、明辨是非
二 :△ ABC是等腰直角三角形 (AB=AC, ∠ BAC=90°),AD是底 边BC上的高,标出∠ B, ∠ C, ∠ BAD, ∠ DAC的度数?
三:在△ ABC中,AB=AD=DC, ∠BAD=16°,求∠ B和∠ C的度数
B
A
C
D
B
D
C
A
巩固练习
答: ∠ B= ∠ C= ∠ BAD= ∠ DAC=45°
答:∠ B= 82° ,∠ C =41°
A
C
B
D
如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说∠C 的度数也是37°.
②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.
请同学们想想,工人师傅的说法对吗?请说明理由.
如图,已知AB=AC,∠BAC=1100,AD是△ABC的中线。
(1)求∠1和∠2的度数;
(2)AD⊥BC吗?为什么?
A
B
C
D
1
2
(1)解:在△ABC ∵AB=AC(已知)
又∵AD是△ABC的中线(已知)
∴ ∠1=∠2= ∠BAC(等腰三角形底边上的中线平分顶角)
∵ ∠BAC=1100(已知)
∴ ∠1=∠2=550(等式性质)。
(2)在△ABC ∵AB=AC(已知)
又∵AD是△ABC的中线(已知)
∴ AD⊥BC(等腰三角形底边上的中线垂直底边)。
我思,我进步
1
一题多解
如图,点D、E在△ABC的边BC上,
且AB=AC,AD=AE,此时BD与CE有
何关系?请说明理由。
谈谈你的收获!
轴对称图形
性质一:两个底角相等(等边对角)
性质二:顶角平分线、底边上的中线、
和底边上的高互相重合(三线合 一)
等腰三角形
小 结
下课了!
谢谢指导
再 见
A
C
B
腰
腰
底边
顶角
底角
底角
等腰三角形的有关概念
返回
学习目标
1、了解等腰三角形的概念, 掌握等腰三角形的性质
2、会运用等腰三角形的概念及性质解决相关问题。
有两条边相等的三角形叫做等腰三角形.
回忆
三角形的中线、角平分线和高线
如图:中线AD,角平分线AE,高AF
(1)什么是等腰三角形?
(2)等腰三角形的有关概念
(3)三角形中学过哪些重要线段?
如图:把一张长方形纸片按图中的虚线对折,
并剪去红线下方的部分,再把它展 开,得△ABC
A
C
D
B
观察
AC和AB有什么关系?这个三角形有什么特点?
AC=AB, △ABC是等腰三角形
心灵手巧
相信你:
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
找一找
等腰三角形是轴对称图形吗?
思考
是
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗?
大胆猜想
猜想与论证
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的 三角形?
猜想
A
B
C
D
A
B
C
则有∠1= ∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
A
B
C
则有 BD= CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法二
A
B
C
则有 ∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
方法三
归纳结论
等腰三角形的两个底角相等。
性质1
(等边对等角)
用符号语言表示为:
在△ABC中,
∵ AC=AB(已知)
∴ ∠B=∠C (等边对等角)
A
B
C
看谁算得快
如图,在下列等腰三角形中,分别求
出它们的底角的度数。
A
B
C
120°
A
B
C
36°
⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。
75°, 30°
70°,40°或55°,55°
35°,35°
巩固练习(1)
想一想:
刚才的证明除了能得到∠B=∠C 你还能发现什么?
重合的线段
重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
猜想:等腰三角形的顶角平分线,
底边上的中线,底边上的高互相重合
A
B
C
则有∠1= ∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ BD=CD
∠ADB =∠ADC=
90°
论证猜想
(等腰三角形三线合一)
等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合
性质2:
归纳结论
用符号语言表示为:
在△ABC中,AB =AC, 点 D在BC上
1、∵AD ⊥ BC
∴∠ = ∠ , = 。
2、∵AD是中线,
∴ ⊥ ,∠ =∠ 。
3、∵AD是角平分线,
∴ ⊥ , = 。
A
B
C
D
⌒
⌒
1
2
1
2
1
2
BD
CD
AD
BC
1
2
AD
BC
BD
CD
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合!
三线合一
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
为什么不一样?
深入分析
例1、如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数。
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD (等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,∠ABC=∠C=72°
x
⌒
2x
⌒
2x
⌒
⌒
2x
1、等腰三角形的顶角一定是锐角。
2、等腰三角形的底角可能是锐角或者直角、
钝角都可以。
3、等腰三角形的顶角平分线一定垂直底边。
4、等腰三角形的角平分线、中线和高互相重
合。
5、等腰三角形底边上的中线一定平分顶角
(X)
(X)
(√)
(X)
(√)
一、明辨是非
二 :△ ABC是等腰直角三角形 (AB=AC, ∠ BAC=90°),AD是底 边BC上的高,标出∠ B, ∠ C, ∠ BAD, ∠ DAC的度数?
三:在△ ABC中,AB=AD=DC, ∠BAD=16°,求∠ B和∠ C的度数
B
A
C
D
B
D
C
A
巩固练习
答: ∠ B= ∠ C= ∠ BAD= ∠ DAC=45°
答:∠ B= 82° ,∠ C =41°
A
C
B
D
如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说∠C 的度数也是37°.
②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.
请同学们想想,工人师傅的说法对吗?请说明理由.
如图,已知AB=AC,∠BAC=1100,AD是△ABC的中线。
(1)求∠1和∠2的度数;
(2)AD⊥BC吗?为什么?
A
B
C
D
1
2
(1)解:在△ABC ∵AB=AC(已知)
又∵AD是△ABC的中线(已知)
∴ ∠1=∠2= ∠BAC(等腰三角形底边上的中线平分顶角)
∵ ∠BAC=1100(已知)
∴ ∠1=∠2=550(等式性质)。
(2)在△ABC ∵AB=AC(已知)
又∵AD是△ABC的中线(已知)
∴ AD⊥BC(等腰三角形底边上的中线垂直底边)。
我思,我进步
1
一题多解
如图,点D、E在△ABC的边BC上,
且AB=AC,AD=AE,此时BD与CE有
何关系?请说明理由。
谈谈你的收获!
轴对称图形
性质一:两个底角相等(等边对角)
性质二:顶角平分线、底边上的中线、
和底边上的高互相重合(三线合 一)
等腰三角形
小 结
下课了!
谢谢指导
再 见
A
C
B
腰
腰
底边
顶角
底角
底角
等腰三角形的有关概念
返回
