人教版数学八年级上册12.3角平分线的性质课件(19张)
文档属性
| 名称 | 人教版数学八年级上册12.3角平分线的性质课件(19张) |  | |
| 格式 | ppt | ||
| 文件大小 | 104.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 09:42:35 | ||
图片预览

文档简介
12.3 角平分线的性质
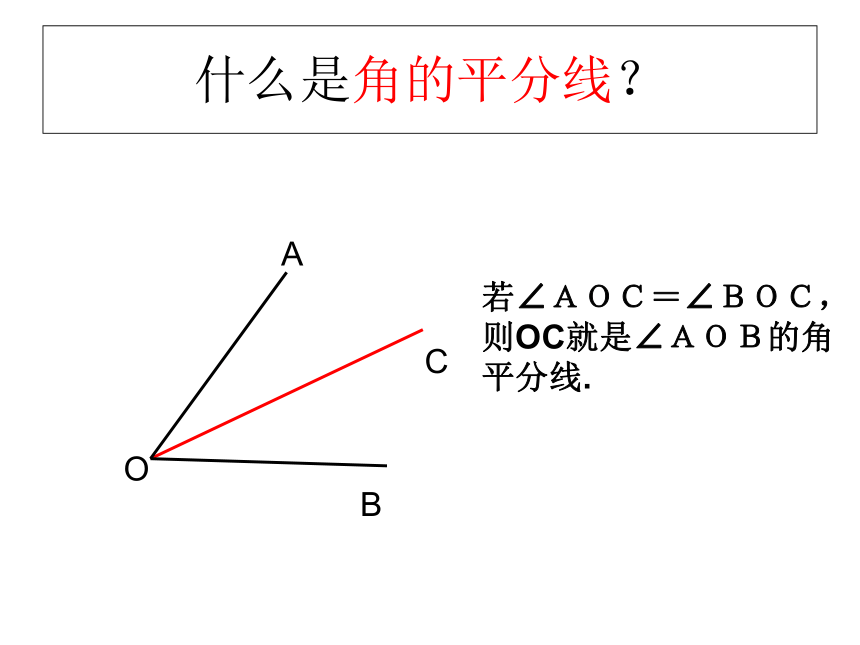
什么是角的平分线?
A
O
B
C
若∠AOC=∠BOC,则OC就是∠AOB的角平分线.
A
O
B
C
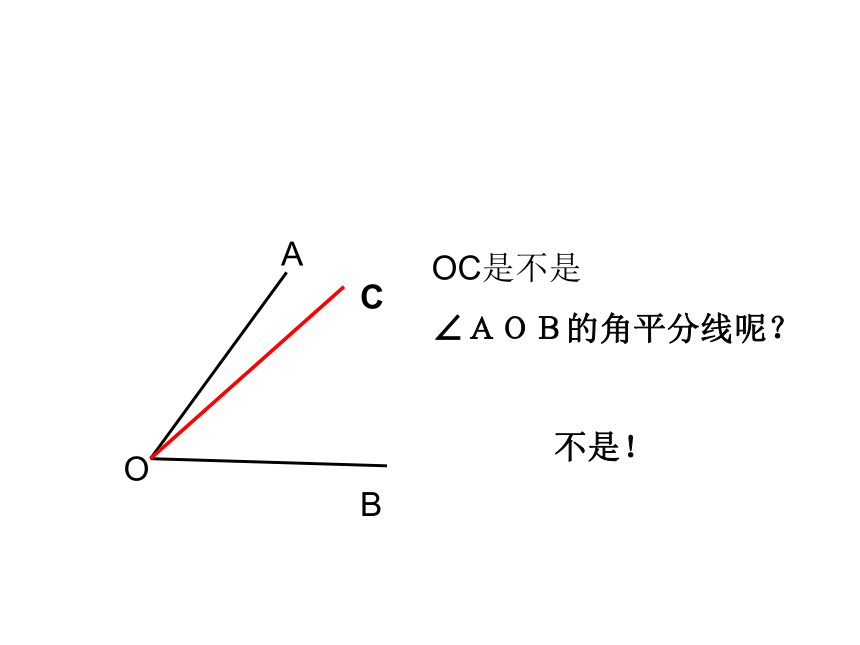
OC是不是
∠AOB的角平分线呢?
不是!
A
O
B
E
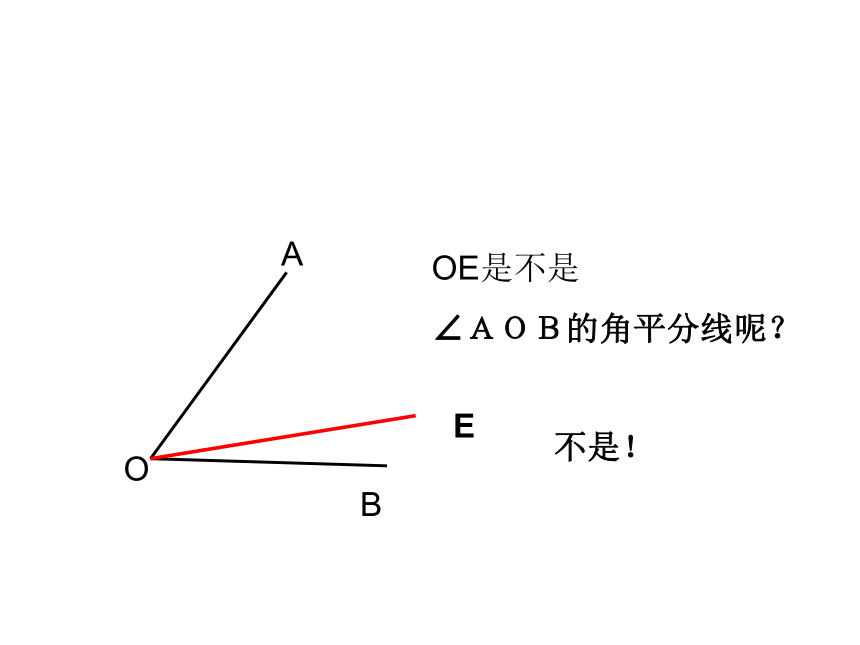
OE是不是
∠AOB的角平分线呢?
不是!
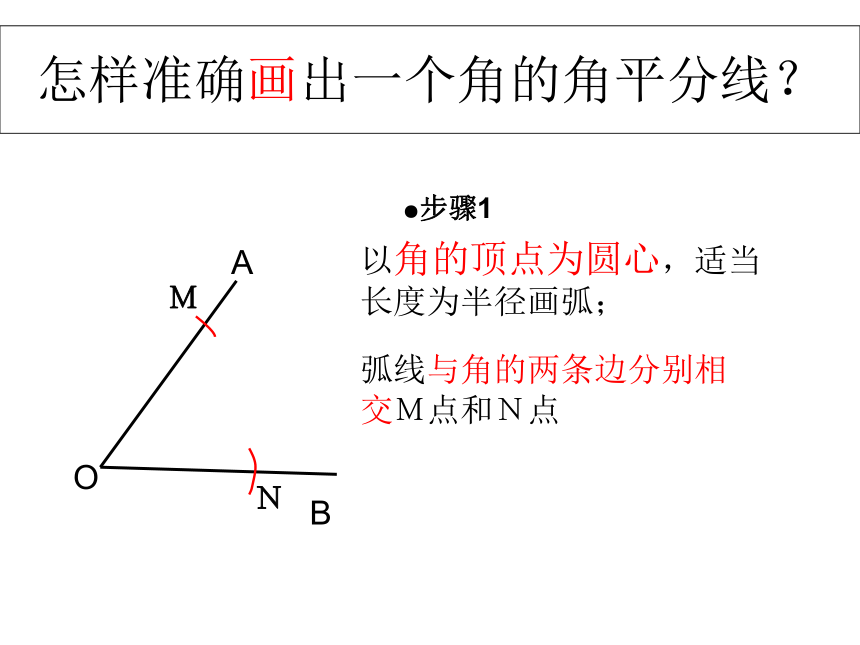
怎样准确画出一个角的角平分线?
以角的顶点为圆心,适当长度为半径画弧;
弧线与角的两条边分别相交M点和N点
A
O
B
M
N
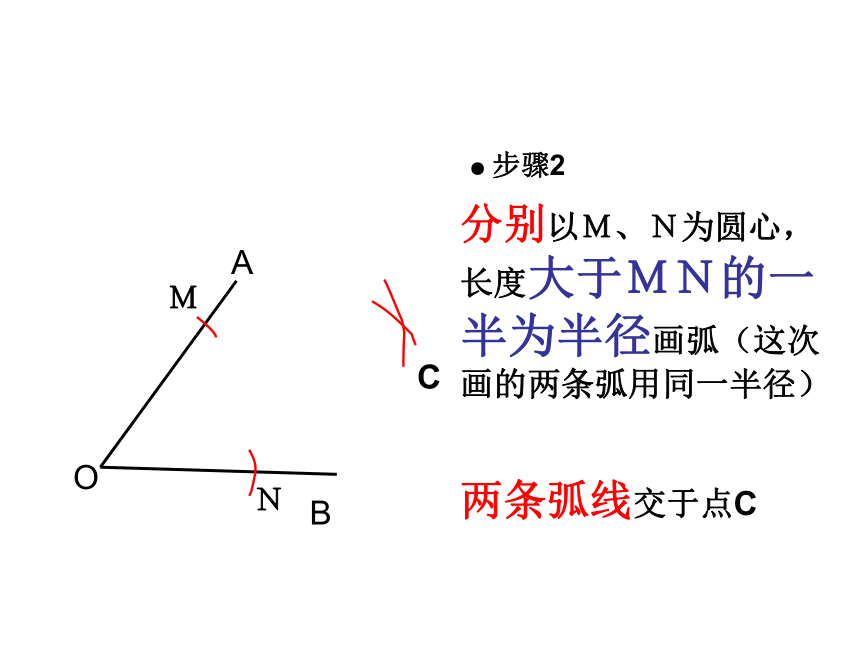
●步骤1
A
O
B
M
N
分别以M、N为圆心,长度大于MN的一半为半径画弧(这次画的两条弧用同一半径)
两条弧线交于点C
C
● 步骤2
A
O
B
M
N
C
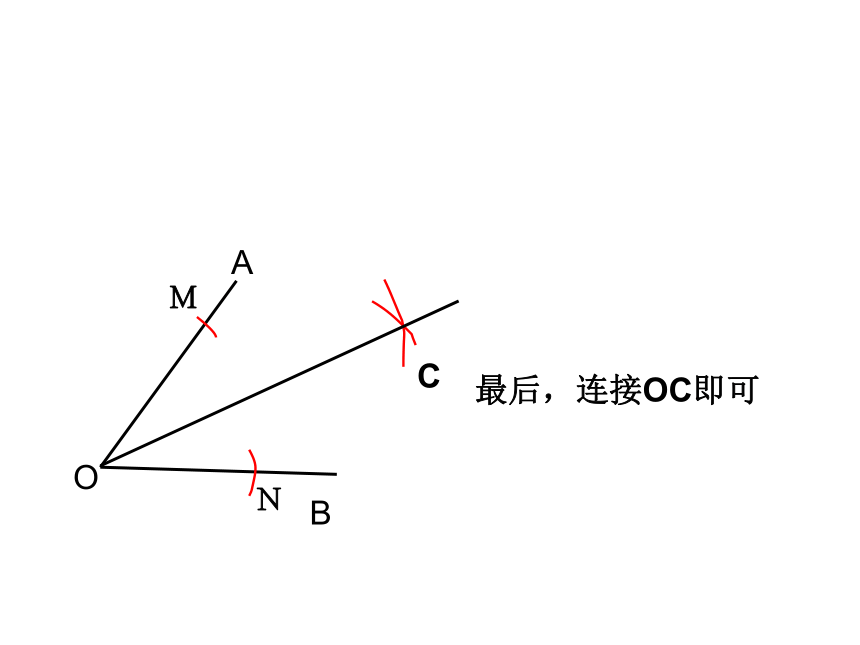
最后,连接OC即可
A
O
B
M
N
C
在△ MOC和△ NOC中
OC=OC(公共边)
∴ △ MOC ≌ △ NOC
即OC是∠AOB的角平分线
(SSS)
MO=NO (同一半径)
MC= NC (另一半径)
∴∠1= ∠ 2(对应角)
为什么这样画出来的OC就是角平分线呢?
1
2
D
E
A
O
B
C
P
想一想:
两条直角边
PE与PD相等吗?
1
2
D
E
A
O
B
C
P
想一想:
两条直角边
PE与PD还相等吗?
A
O
B
C
P
E
D
想一想:
两条直角边
PE与PD还相等吗?
D
E
A
O
B
C
P
1
2
两条直角边之所以相等,原因如下
∠1= ∠2(角平分线得到的)
OP= OP(公共边)
3
4
∠3= ∠4(垂直得到)
△OPD≌△OPE(AAS)
PD=PE
角的平分线的性质
P49
注意关键点:
1、角平分线上的点
2、刚刚好到角的两边(长了短了都不行)
3、到角的两边的距离(直角边)
思考:如果不是垂直画那两条线,还会相等吗?
P
E
D
A
O
B
C
1
2
关键一点:利用全等(AAS)
1
2
A
O
B
C
P
E
D
3
4
练习
《名师金典》P36 - 37 1、2、 3
提升能力 1
A
D
F
C
B
E
证明:∵AD是角平分线
并且DE AB,DF AC
∴DE=DF
在Rt △BED 和Rt △CFD 中
(角平分线的性质)
BD=DC(斜边)
DE=DF(直角边)
∴ Rt △BED ≌ R t △CFD(HL)
∴BE=FC(对应边)
如图, BP平分∠ABC ,CE AB , AD BC
求证: △AEP ≌ △CDP
B
C
D
A
E
P
1
2
证明:∵BP是角平分线
并且CE AB,AD BC
∴PE=PD
(角平分线的性质)
在△AEP 和 △C DP 中
∠ 1= ∠2=900
PE=PD
∠ APE= ∠ CPD(对顶角)
∴ △BED ≌ △CFD(ASA)
如图,AD平分∠EBC,DE⊥AE , DF⊥AC,BD=CD
求证: △BED ≌ △CFD
E
D
C
B
A
F
证明:∵AD是角平分线
并且DE AB,DF AC
∴DE=DF
(角平分线的性质)
在Rt △BED 和Rt △CFD 中
BD=DC(斜边)
DE=DF(直角边)
∴ Rt △BED ≌ R t △CFD(HL)
如图, DA平分∠BAC ,DC AC ,
DE AB,AC=BC,若AB=6cm,
则△BDE的周长是_____ cm.
A
C
D
B
E
什么是角的平分线?
A
O
B
C
若∠AOC=∠BOC,则OC就是∠AOB的角平分线.
A
O
B
C
OC是不是
∠AOB的角平分线呢?
不是!
A
O
B
E
OE是不是
∠AOB的角平分线呢?
不是!
怎样准确画出一个角的角平分线?
以角的顶点为圆心,适当长度为半径画弧;
弧线与角的两条边分别相交M点和N点
A
O
B
M
N
●步骤1
A
O
B
M
N
分别以M、N为圆心,长度大于MN的一半为半径画弧(这次画的两条弧用同一半径)
两条弧线交于点C
C
● 步骤2
A
O
B
M
N
C
最后,连接OC即可
A
O
B
M
N
C
在△ MOC和△ NOC中
OC=OC(公共边)
∴ △ MOC ≌ △ NOC
即OC是∠AOB的角平分线
(SSS)
MO=NO (同一半径)
MC= NC (另一半径)
∴∠1= ∠ 2(对应角)
为什么这样画出来的OC就是角平分线呢?
1
2
D
E
A
O
B
C
P
想一想:
两条直角边
PE与PD相等吗?
1
2
D
E
A
O
B
C
P
想一想:
两条直角边
PE与PD还相等吗?
A
O
B
C
P
E
D
想一想:
两条直角边
PE与PD还相等吗?
D
E
A
O
B
C
P
1
2
两条直角边之所以相等,原因如下
∠1= ∠2(角平分线得到的)
OP= OP(公共边)
3
4
∠3= ∠4(垂直得到)
△OPD≌△OPE(AAS)
PD=PE
角的平分线的性质
P49
注意关键点:
1、角平分线上的点
2、刚刚好到角的两边(长了短了都不行)
3、到角的两边的距离(直角边)
思考:如果不是垂直画那两条线,还会相等吗?
P
E
D
A
O
B
C
1
2
关键一点:利用全等(AAS)
1
2
A
O
B
C
P
E
D
3
4
练习
《名师金典》P36 - 37 1、2、 3
提升能力 1
A
D
F
C
B
E
证明:∵AD是角平分线
并且DE AB,DF AC
∴DE=DF
在Rt △BED 和Rt △CFD 中
(角平分线的性质)
BD=DC(斜边)
DE=DF(直角边)
∴ Rt △BED ≌ R t △CFD(HL)
∴BE=FC(对应边)
如图, BP平分∠ABC ,CE AB , AD BC
求证: △AEP ≌ △CDP
B
C
D
A
E
P
1
2
证明:∵BP是角平分线
并且CE AB,AD BC
∴PE=PD
(角平分线的性质)
在△AEP 和 △C DP 中
∠ 1= ∠2=900
PE=PD
∠ APE= ∠ CPD(对顶角)
∴ △BED ≌ △CFD(ASA)
如图,AD平分∠EBC,DE⊥AE , DF⊥AC,BD=CD
求证: △BED ≌ △CFD
E
D
C
B
A
F
证明:∵AD是角平分线
并且DE AB,DF AC
∴DE=DF
(角平分线的性质)
在Rt △BED 和Rt △CFD 中
BD=DC(斜边)
DE=DF(直角边)
∴ Rt △BED ≌ R t △CFD(HL)
如图, DA平分∠BAC ,DC AC ,
DE AB,AC=BC,若AB=6cm,
则△BDE的周长是_____ cm.
A
C
D
B
E
