人教版数学九年级 上册23.2.1中心对称课件(19张ppt)
文档属性
| 名称 | 人教版数学九年级 上册23.2.1中心对称课件(19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 419.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 16:17:43 | ||
图片预览



文档简介
中心对称
九年级数学23.2.1:
回忆一下:
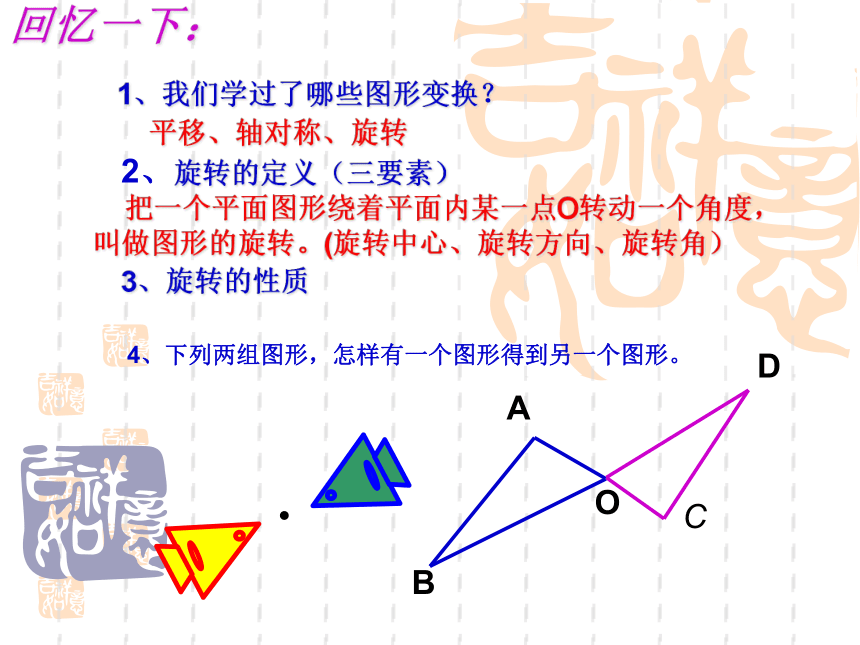
1、我们学过了哪些图形变换?
平移、轴对称、旋转
2、旋转的定义(三要素)
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转。(旋转中心、旋转方向、旋转角)
3、旋转的性质
O
A
B
C
D
4、下列两组图形,怎样有一个图形得到另一个图形。
23.2.1
中心对称
1.理解并掌握中心对称的概念和
性质。
2.会画一个图形关于中心对称的 图形。
目标:
O
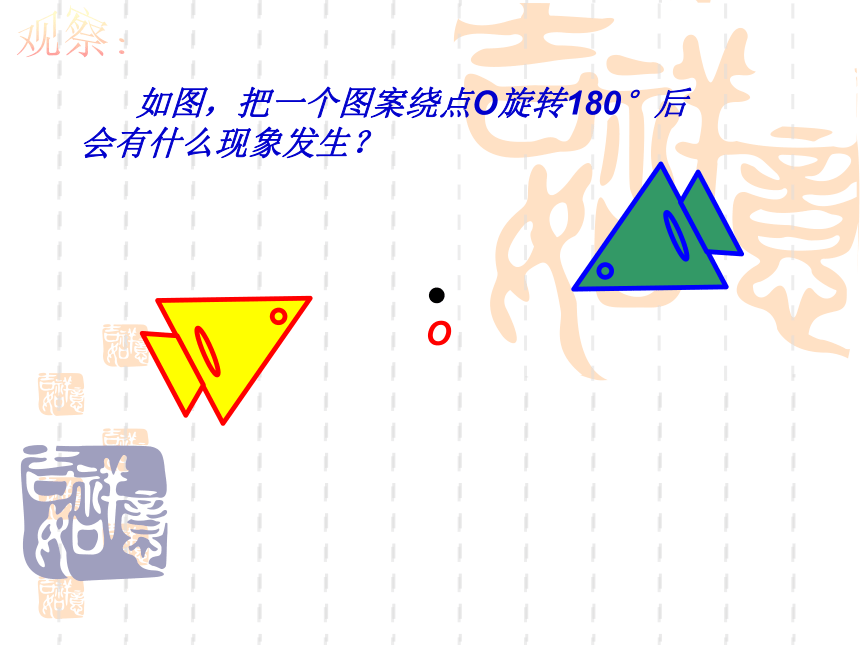
如图,把一个图案绕点O旋转180°后
会有什么现象发生?
观察:
O
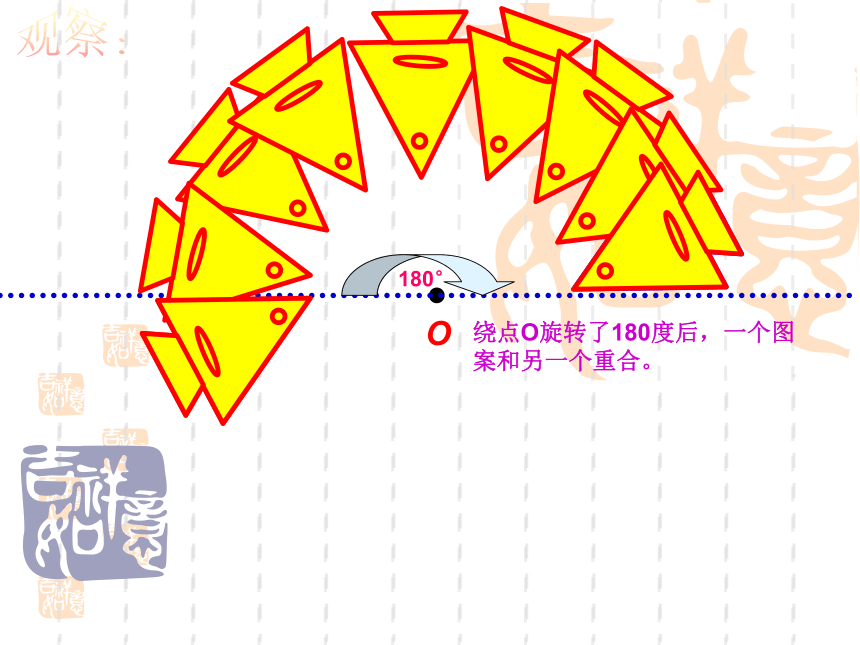
绕点O旋转了180度后,一个图
案和另一个重合。
180°
观察:
观察:
A
B
C
D
O
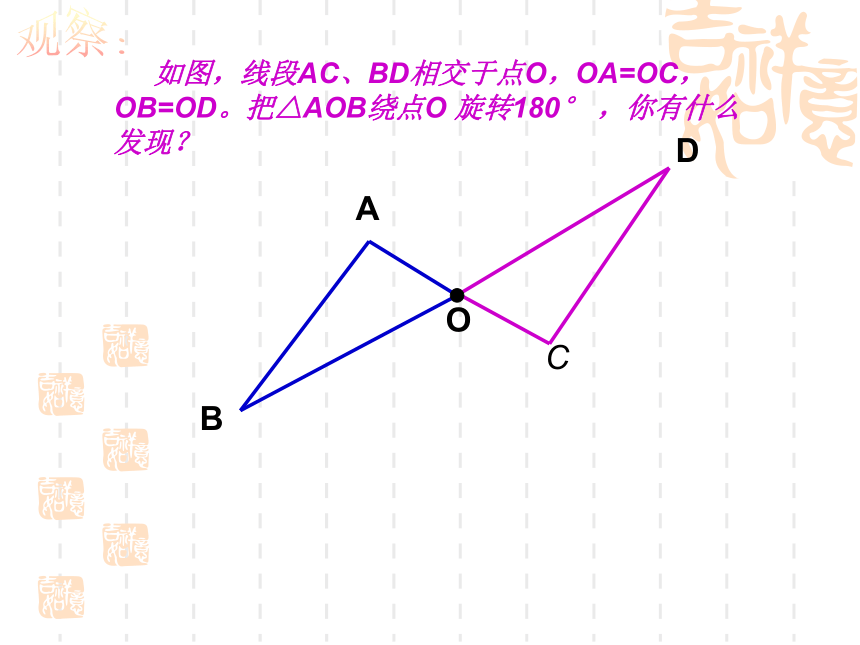
如图,线段AC、BD相交于点O,OA=OC,OB=OD。把△AOB绕点O 旋转180° ,你有什么发现?
观察:
A
B
C
D
O
180°
△AOB 绕点O旋转180° 后与△COD重合。
像这样,把一个图形绕着某一个点旋转180° ,如果它能够与另一个图形重合,那么就说这 两个图形 关于这个点对称或 中心对称。
这个点叫做 对称中心。
这两个图形中的 对应点叫做
关于中心的对称点。
定义:
中心对称是旋转的特殊情况(旋转180°)
想一想:
A
B
C
D
O
1.△AOB 绕点O旋转180° 后与△COD重合。那么△AOB 与△COD有什么关系?
关于点O对称或中心对称。
2.它们的对称中心是
( )
3.哪些点是关于
点O的对称点?
点O
点A与点C
点B与点D
点O与点O
O
A
B
C
D
E
F
已知△ABC和△DEF绕点O旋转180度后能互相重合。回答下列问题:
小试牛刀
1.这两个图形是什么关系?
中心对称
2.它们的对称中心是
( )
点O
3.哪些点是关于点O的对称点?
点A与点D
点B与点F
点C与点E
如图,旋转三角板。画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出
△A’ B’C’;
第三步,移开三角板。
探究:
B
C
A
A’
B’
C’
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
0
这样画出的两个三角形关于点O对称,
分别连接A A’ 、B B’ 、C C’ 。
点O在线段上吗?如果在,在什么位置?
C
A
B
A’
B’
C’
0
点O在线段A A’ 、B B’ 、C C’上,并且
点O是线段A A’ 、B B’ 、C C’的中点。
△ ABC与△A’ B’C’有什么关系?
全 等
O
A
B
C
D
E
F
已知△ABC和△DEF关于点O对称。回答下列问题:
归纳:
1.对称点所连线段与点O
有什么关系?
对称点所连线段经过点O。
并且被点O平分。
1.关于中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分。
2.关于中心对称的两个图形是全等形。
2.△ABC和△DEF有何关系?
全 等
可以得出:
例题:
(1)如图1,选择点O为对称中心,画出点A关于点O的对称点A’ 。
A
O
图1
解:1.连接AO并延长。
2.在AO的延长线
上截取O A’ =OA。
点A’ 即为所求。
A’
例题:
(2)如图2,选择点O为对称中心,画出与△ ABC关于点O对称的△A’ B’C’.
图2
O
C
B
A
C’
A’
B’
△A’ B’C’即为所求。
练习:
1、分别画出下列图形关于点O对称的图形。
2、图中的两个四边形关于某点对称,找出它们的对称中心。
A
B
C
O
A
B
O
A
B
C
O
3、下列说法正确的是( )
A、全等的两个图形成中心对称。
B、成中心对称的两个图形一定全等。
C、旋转后能重合的两个图形中心对称。
D、关于某点成中心对称的两图形平移后可以重合。
4、如右图,在平行四边形ABCD中,
点A与点( )关于点( )成中心对称;
△ABO与( )关于( )成中心对称。
A
B
C
D
O
B
C
O
△CDO
点O
1.如图所示,△ABC与△A′B′C′是中心对称的两个图形,下列说法不正确的是( )
A.S△ABC=S△A′B′C′ B.AB=A′B′
C.AB∥A′B′ D.S△ABO=S△A′B′C′
2. 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,若AB=3,BC=4,那么阴影部分的面积为 ( )
A.4 B.12 C.6 D.3
3.如图,△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在点C′处,则CC′的长为( )
A. B. 4 C. D.
自我检测
课堂小结:
作业:
课本69页第1题,练习册49页练习。
1、中心对称的定义;
2、中心对称的性质?。
3、中心对称作图的方法.
九年级数学23.2.1:
回忆一下:
1、我们学过了哪些图形变换?
平移、轴对称、旋转
2、旋转的定义(三要素)
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转。(旋转中心、旋转方向、旋转角)
3、旋转的性质
O
A
B
C
D
4、下列两组图形,怎样有一个图形得到另一个图形。
23.2.1
中心对称
1.理解并掌握中心对称的概念和
性质。
2.会画一个图形关于中心对称的 图形。
目标:
O
如图,把一个图案绕点O旋转180°后
会有什么现象发生?
观察:
O
绕点O旋转了180度后,一个图
案和另一个重合。
180°
观察:
观察:
A
B
C
D
O
如图,线段AC、BD相交于点O,OA=OC,OB=OD。把△AOB绕点O 旋转180° ,你有什么发现?
观察:
A
B
C
D
O
180°
△AOB 绕点O旋转180° 后与△COD重合。
像这样,把一个图形绕着某一个点旋转180° ,如果它能够与另一个图形重合,那么就说这 两个图形 关于这个点对称或 中心对称。
这个点叫做 对称中心。
这两个图形中的 对应点叫做
关于中心的对称点。
定义:
中心对称是旋转的特殊情况(旋转180°)
想一想:
A
B
C
D
O
1.△AOB 绕点O旋转180° 后与△COD重合。那么△AOB 与△COD有什么关系?
关于点O对称或中心对称。
2.它们的对称中心是
( )
3.哪些点是关于
点O的对称点?
点O
点A与点C
点B与点D
点O与点O
O
A
B
C
D
E
F
已知△ABC和△DEF绕点O旋转180度后能互相重合。回答下列问题:
小试牛刀
1.这两个图形是什么关系?
中心对称
2.它们的对称中心是
( )
点O
3.哪些点是关于点O的对称点?
点A与点D
点B与点F
点C与点E
如图,旋转三角板。画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出
△A’ B’C’;
第三步,移开三角板。
探究:
B
C
A
A’
B’
C’
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
0
这样画出的两个三角形关于点O对称,
分别连接A A’ 、B B’ 、C C’ 。
点O在线段上吗?如果在,在什么位置?
C
A
B
A’
B’
C’
0
点O在线段A A’ 、B B’ 、C C’上,并且
点O是线段A A’ 、B B’ 、C C’的中点。
△ ABC与△A’ B’C’有什么关系?
全 等
O
A
B
C
D
E
F
已知△ABC和△DEF关于点O对称。回答下列问题:
归纳:
1.对称点所连线段与点O
有什么关系?
对称点所连线段经过点O。
并且被点O平分。
1.关于中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分。
2.关于中心对称的两个图形是全等形。
2.△ABC和△DEF有何关系?
全 等
可以得出:
例题:
(1)如图1,选择点O为对称中心,画出点A关于点O的对称点A’ 。
A
O
图1
解:1.连接AO并延长。
2.在AO的延长线
上截取O A’ =OA。
点A’ 即为所求。
A’
例题:
(2)如图2,选择点O为对称中心,画出与△ ABC关于点O对称的△A’ B’C’.
图2
O
C
B
A
C’
A’
B’
△A’ B’C’即为所求。
练习:
1、分别画出下列图形关于点O对称的图形。
2、图中的两个四边形关于某点对称,找出它们的对称中心。
A
B
C
O
A
B
O
A
B
C
O
3、下列说法正确的是( )
A、全等的两个图形成中心对称。
B、成中心对称的两个图形一定全等。
C、旋转后能重合的两个图形中心对称。
D、关于某点成中心对称的两图形平移后可以重合。
4、如右图,在平行四边形ABCD中,
点A与点( )关于点( )成中心对称;
△ABO与( )关于( )成中心对称。
A
B
C
D
O
B
C
O
△CDO
点O
1.如图所示,△ABC与△A′B′C′是中心对称的两个图形,下列说法不正确的是( )
A.S△ABC=S△A′B′C′ B.AB=A′B′
C.AB∥A′B′ D.S△ABO=S△A′B′C′
2. 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,若AB=3,BC=4,那么阴影部分的面积为 ( )
A.4 B.12 C.6 D.3
3.如图,△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在点C′处,则CC′的长为( )
A. B. 4 C. D.
自我检测
课堂小结:
作业:
课本69页第1题,练习册49页练习。
1、中心对称的定义;
2、中心对称的性质?。
3、中心对称作图的方法.
同课章节目录
