人教版数学九年级上册24.1.1 圆课件(共19张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.1.1 圆课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 560.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 14:13:50 | ||
图片预览



文档简介
圆与圆的位置关系
初步感知
圆与圆有哪几种位置关系?
探究一
验证
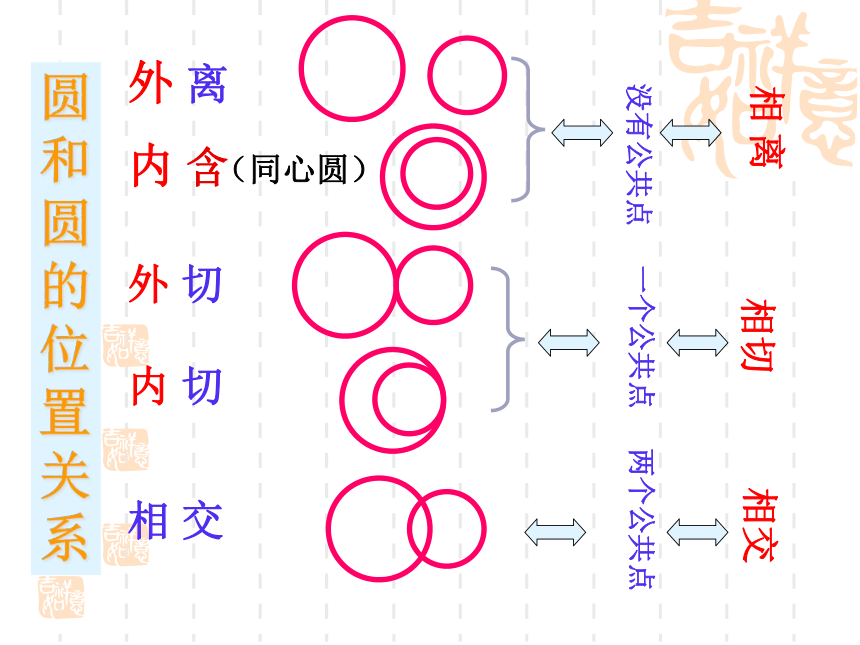
圆
和
圆
的
位
置
关
系
没有公共点
一个公共点
两个公共点
相 离
相切
相交
外 离
内 含
内 切
外 切
相 交
(同心圆)
动动脑发现(举例子)
(自行车轮、奥运五环、滑轮组、望远镜、纸筒、光碟……) 。
举例说说圆和圆的位置关系在生活动中的应用。
牛刀小试
1.下列说法中正确的有( )
(1)两圆有两个公共点,则两圆相交
(2)若两圆只有一个公共点,则两圆外切。
(3)若两圆没有公共点,则两圆外离。
(4)若两圆有三个公共点,则两圆重合
A 1个 B 2个 C 3 个 D4个
B
图形中没有哪种位置关系?
欣赏
1、认识圆心距[两圆圆心之间的距离叫做圆心距]
2、先积极思考再结合多媒体动画探索规律。
外离 d>R+r
外切 d=R+r(先掌握)
相交 R-r 内切 d=R-r(先掌握)
内含 d (让学生用自己的语言来表达,师生小结)
探究二:探索d和R , r 的数量关系
位置关系
d 和R、 r关系
交点
两圆外离
d >R+ r
0
两圆外切
d =R+ r
1
两圆相交
R? r2
两圆内切
d = R? r
1
两圆内含
0≤ dr)
0
性质
判定
两圆位置关系的性质与判定:
练习:
1, 填表
两圆位置关系
外离
内切
外切
内含
相交
已知:如图⊙O的半径为OA=5cm,点p是圆外一点,op=8cm。
求:(1)以p为圆心作⊙P与⊙O外切,⊙ P的半径
是多少?(2)以P为圆心作⊙P与⊙O内切, ⊙ P的半径是多少?
o
p
A
?
?
解:
设两圆外切于A,则OP=OA+AP
∴AP=OP-OA=8-5=3(cm)
即小圆P的半径是3cm。
?
例题
o
p
?
B
(2)
解:设两圆内切于B,则OP=BP-OB
∴ BP=OP+OB=8+5=13(cm),
即大圆P的半径是13cm。
?
若上题改为“以P为圆心作⊙P与⊙O相切”呢?
变形
判别两圆关系
2, 若两圆的圆心距
两圆半径是方程
两根,则两圆位置关系为 .
外离
3, 若两圆的半径为
圆心距 满足
则两圆位置关系为 .
外切或内切
4,⊙
⊙
⊙
⊙
.
内含
d=6
X-5x+1=0 的
2
R+d – r =2Rd
2
2
2
=
=
课堂小结
(1) 理解并掌握两圆的五种位置关系及其特征
(2)理解并掌握两圆的圆心距d与两圆的半径R,r的数量关系
(3)会判定两圆的五种位置关系
作业:
习题24.2 P102 7 13
P103 17
初步感知
圆与圆有哪几种位置关系?
探究一
验证
圆
和
圆
的
位
置
关
系
没有公共点
一个公共点
两个公共点
相 离
相切
相交
外 离
内 含
内 切
外 切
相 交
(同心圆)
动动脑发现(举例子)
(自行车轮、奥运五环、滑轮组、望远镜、纸筒、光碟……) 。
举例说说圆和圆的位置关系在生活动中的应用。
牛刀小试
1.下列说法中正确的有( )
(1)两圆有两个公共点,则两圆相交
(2)若两圆只有一个公共点,则两圆外切。
(3)若两圆没有公共点,则两圆外离。
(4)若两圆有三个公共点,则两圆重合
A 1个 B 2个 C 3 个 D4个
B
图形中没有哪种位置关系?
欣赏
1、认识圆心距[两圆圆心之间的距离叫做圆心距]
2、先积极思考再结合多媒体动画探索规律。
外离 d>R+r
外切 d=R+r(先掌握)
相交 R-r
内含 d
探究二:探索d和R , r 的数量关系
位置关系
d 和R、 r关系
交点
两圆外离
d >R+ r
0
两圆外切
d =R+ r
1
两圆相交
R? r
两圆内切
d = R? r
1
两圆内含
0≤ d
0
性质
判定
两圆位置关系的性质与判定:
练习:
1, 填表
两圆位置关系
外离
内切
外切
内含
相交
已知:如图⊙O的半径为OA=5cm,点p是圆外一点,op=8cm。
求:(1)以p为圆心作⊙P与⊙O外切,⊙ P的半径
是多少?(2)以P为圆心作⊙P与⊙O内切, ⊙ P的半径是多少?
o
p
A
?
?
解:
设两圆外切于A,则OP=OA+AP
∴AP=OP-OA=8-5=3(cm)
即小圆P的半径是3cm。
?
例题
o
p
?
B
(2)
解:设两圆内切于B,则OP=BP-OB
∴ BP=OP+OB=8+5=13(cm),
即大圆P的半径是13cm。
?
若上题改为“以P为圆心作⊙P与⊙O相切”呢?
变形
判别两圆关系
2, 若两圆的圆心距
两圆半径是方程
两根,则两圆位置关系为 .
外离
3, 若两圆的半径为
圆心距 满足
则两圆位置关系为 .
外切或内切
4,⊙
⊙
⊙
⊙
.
内含
d=6
X-5x+1=0 的
2
R+d – r =2Rd
2
2
2
=
=
课堂小结
(1) 理解并掌握两圆的五种位置关系及其特征
(2)理解并掌握两圆的圆心距d与两圆的半径R,r的数量关系
(3)会判定两圆的五种位置关系
作业:
习题24.2 P102 7 13
P103 17
同课章节目录
