新青岛版八年级上册数学第2章-图形的轴对称-复习课件(41张)
文档属性
| 名称 | 新青岛版八年级上册数学第2章-图形的轴对称-复习课件(41张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览










文档简介
(共41张PPT)
复习
1、什么叫轴对称?什么叫做两个图形关于某一条直线成轴对称?什么叫轴对称图形?“轴对称图形”与“两个图形关于某一条直线成轴对称”有什么区别?
2、轴对称的基本性质是什么?如何画一个图形关于某条直线对称的图形?
3、在直角坐标系中,点P(x,y)关于x轴和y轴的对称点的坐标有什么特点?
知识点回顾
4、什么叫线段的垂直平分线?线段的垂直平分线有什么性质?它的逆命题是什么?如何用尺规作线段的垂直平分线?
过一点作已知直线的垂线?
5、角的平分线具有什么性质?它的逆命题是什么?如何做角平分线?
6、等腰三角形有哪些性质?等边三角形呢?怎样判断一个三角形是等腰三角形或等边三角形?已知哪些条件,
可以用尺规做出等腰三角形?
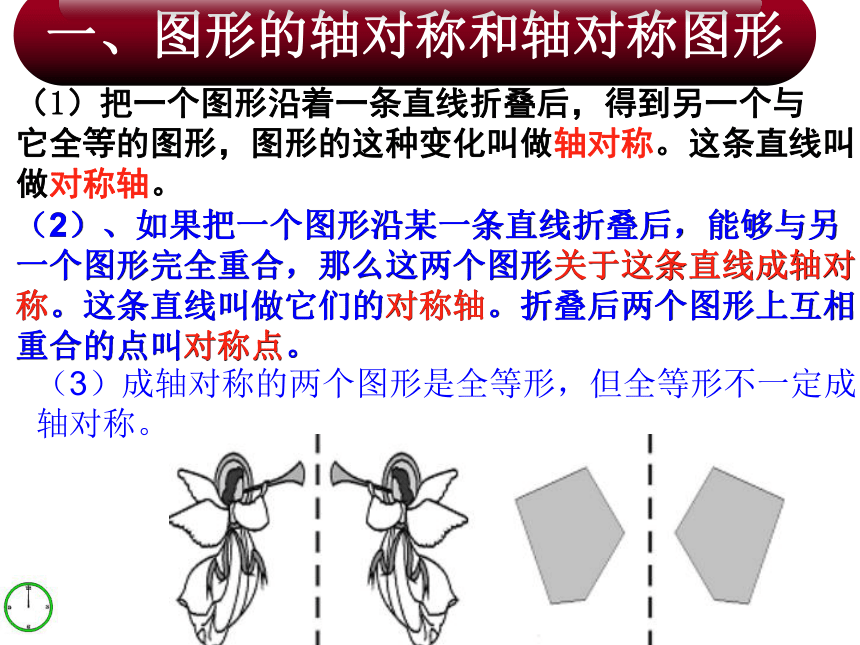
(2)、如果把一个图形沿某一条直线折叠后,能够与另一个图形完全重合,那么这两个图形关于这条直线成轴对称。这条直线叫做它们的对称轴。折叠后两个图形上互相重合的点叫对称点。
(1)把一个图形沿着一条直线折叠后,得到另一个与
它全等的图形,图形的这种变化叫做轴对称。这条直线叫
做对称轴。
(3)成轴对称的两个图形是全等形,但全等形不一定成轴对称。
一、图形的轴对称和轴对称图形
(4)、如果一个图形沿某一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴,对折后图形上能够重合的点叫对称点。
例题1
l
75°
γ
a
b
δ
2.29
3.20
3.44
c
β
43°
α
右图中两个三角形关于直线l成轴对称。如果三角形的部分边长(单位:厘米)和角的度数如图所示,求未知的边长和角的度数。
解:因为这两个三角形关于直线l成轴对称,它们的对应角相等,对应线段相等,所以
a=3.20厘米,b=3.44厘米,c=2.29厘米;
∠α=75°,∠γ=43°。
又因为三角形的内角和为180°,所以
∠δ=∠β=180°-75°-43°=62°
区别:轴对称图形是指一个具有特殊形状的图形,对称轴不只一条;两个图形关于某一条直线成轴对称是指两个图形的特殊形状和位置关系,对称轴只有一条。
联系:
①都有一条直线,都沿直线折叠重合;②若把轴对称图形沿对称轴分成两部分,则这两个图形关于这条直线成轴对称;若把两个关于某直线成轴对称的图形看作一个整体,则它就是一个轴对称图形。
(5)、“轴对称图形”与“两个图形关于某一条直线成轴对称”的区别与联系:
(1)成轴对称的两个图形中,对应点的连线被对称轴垂直平分,对应线段相等,对应角相等。
(2)在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
(3)点(x,
y)关于x轴对称的点的坐标为______.
(4)点(x,
y)关于y轴对称的点的坐标为______.
二、轴对称的基本性质
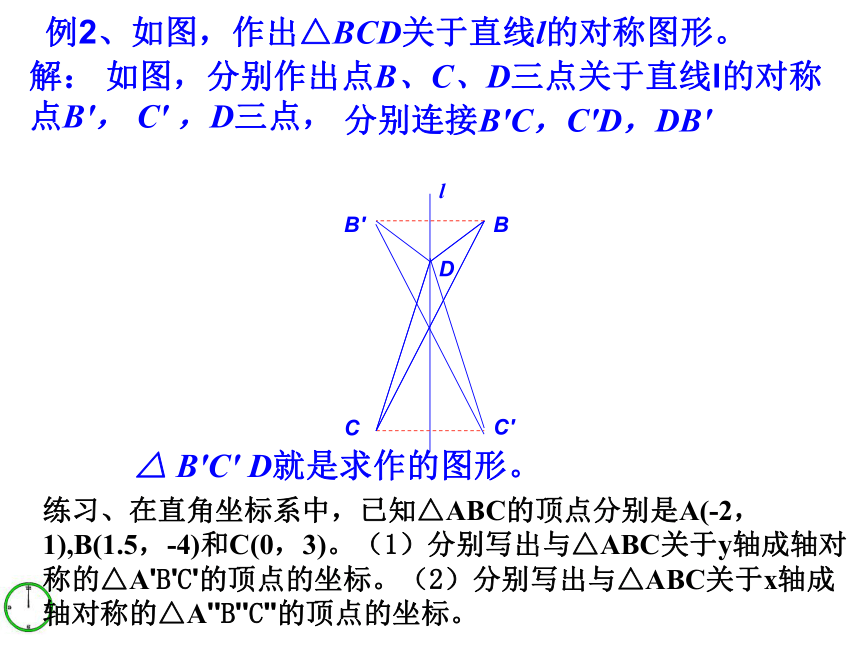
例2、如图,作出△BCD关于直线l的对称图形。
B′
C
C′
B
D
l
解:
如图,分别作出点B、C、D三点关于直线l的对称点B′,
C′
,D三点,
△
B′C′
D就是求作的图形。
分别连接B′C,C′D,DB′
练习、在直角坐标系中,已知△ABC的顶点分别是A(-2,1),B(1.5,-4)和C(0,3)。(1)分别写出与△ABC关于y轴成轴对称的△A'B'C'的顶点的坐标。(2)分别写出与△ABC关于x轴成轴对称的△A''B''C''的顶点的坐标。
A
B
M
N
O
(1)直线MN垂直于线段AB,并且平分线段AB,我们
把直线MN叫做线段AB的垂直平分线。
垂直并且平分一条线段的直线叫做这条线段的垂直平分线,
也叫中垂线。
(2)、线段是轴对称图形,它的一条对称轴是这条线段的垂直平分线。
线段垂直平分线的性质
三、线段垂直平分线
性质定理:线段的垂直平分线上的点,到这条线段两个端点的距离相等
线段垂直平分线的性质与判定
数学语言:
∵CD⊥AB
AE=BE(已知)
∴PA=PB(线段垂直平分线上的任意一点到
这条线段两个端点的距离相等)
判定定理
到一条线段两个端点距离相等的点,在这条线段
的垂直平分线上.
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点
距离相等的点,在这条线段的垂直平分线上).
如图:在△ABC中,已知AC=16,AB的垂直平分线交AB于点D,交AC于点E,BC=14,则△BCE的周长等于多少呢?
B
A
E
D
C
解:
∵
DE是AB的垂直平分线(已知)
∴____=______(______________)
∵AC=16(已知)
∴____________
∵BC=14(已知)
∴
△BCE的周长=______
AE
BE
线段垂直平分线上的任意一点到这条线段两个端点的距离相等
BE+CE=16
30
驶向胜利的彼岸
线段的垂直平分线的作法
已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:
用尺规作线段的垂直平分线.
1.分别以点A和B为圆心,以大于AB/2长为半径作弧,两弧交于点C和D.
A
B
C
D
2.
作直线CD.
则直线CD就是线段AB的垂直平分线.
请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.
老师提示:
因为直线CD与线段AB的交点就是AB的中点,所以我们也用这种方法作线段的中点.
探究
思考
1、如图,点C在直线上,试过点C画出直线的垂线。
2、如图,如果点C不在直线上,试和同学讨论,应采取怎样的步骤,过点C画出直线的垂线?
四、垂线的画法
作法:
(1)任取一点M,使点M和点C在直线L的两侧;
(2)以C点为圆心,以CM长为半径画弧,与直线L交于A、B两点;
(3)分别以A、B两点为圆心,以大于
长为半径画弧,两弧相交于D点;
(4)过C、D两点作直线CD。
所以,直线CD就是所求作的。
角是轴对称图形,角的平分线所在的直线是它的对称轴。
角平分线上的点,到这个角的两边的距离相等。
角的内部到角的两边距离相等的点在角的平分线上。
五、角平分线的性质与判定
等腰三角形是轴对称图形。等腰三角形的对称轴是底边的垂直平分线。
等腰三角形的顶角平分线、底边上的高、底边上的中线重合(也称三线合一)。
等腰三角形的两个底角相等。
等边三角形是轴对称图形.
等边三角形每个角的平分线和这个角的对边上的中线、
高线重合(三线合一),它们所在的直线都是等边
三角形的对称轴.等边三角形共有3条对称轴.
等边三角形的各角都相等,都等于60°
六、等腰三角形
等腰三角形的判定
有两个角相等的三角形是等腰三角形。
(简称“等角对等边”).
3个角相等的三角形是等边三角形.
有两个角等于600的三角形是等边三角形.
有一个角等于600的等腰三角形是等边三角形.
等边三角形的判定
例3.如图,△ABC和△CDE都是等边三角形,且点A,C,E在一条直线上.(1)AD=BE吗?为什么?
(2)△MNC为等边三角形吗?为什么?
A
B
C
D
E
M
N
二、【巩固练习】
1.下列图形中,轴对称图形有(
).
(A)1个
(B)2个
(C)3个
(D)4个
C
3.如图,在△ABC中,∠B=90°,∠A=36°,
AC的垂直平分线MN与AB交于点D,则∠BCD的
度数是____________.
4.已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形
ADBC的周长是
.
5.如图,以正方形ABCD的一边CD为边向形外作等
边三角形CDE,则∠AEB=
.
20cm
6.
等腰三角形ABC中,
(1)若∠A=80°,则∠B=
°;
(2)若周长为8cm,AB=3cm,则BC=
cm
三、【典型例题】
例1、
已知△ABC中,AB=AC=10,DE垂直平分AB,交
AC于E,已知三角形BEC的周长是16.
求三角形ABC的周长.
.
1、等腰三角形一边长为2,周长为8,则腰长为
.
2、
如图1,在△ABC中,AM垂直平分BC,若AB=12,BM=10,则△ABC的周长为
.
3、
如图2,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,若DE=3cm,则DF=
cm.
典型举例(一)概念直接应用类
1、有一个内角为60°的等腰三角形,腰长为6cm,那么这个三角形的周长为___________cm.
2、已知等腰三角形的一边长为6,一个外角为1200,则它的周长为(
)
A、12
B、15
C、16
D、18
3、在“线段、锐角、三角形、等边三角形、”这四个图形中,是轴对称图形的有
个,其中对称轴最多的是
。
4、在Rt△ABC中,斜边上的中线长为5cm,则斜边长为:
5、到三角形的三个顶点距离相等的点是(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
典型举例(二)折叠展开类
1、将一正方形纸片按图中(1)、(2)的方式依次对折后,再沿(3)中的虚线裁剪,最后将(4)中的纸片打开铺平,所得图案应该是下面图案中的(
)
(1)
(2)
(3)
(4)
B
A
C
D
2、认真观察图(7.1)的4个图中阴影部分构成的图案,回答下列问题:图(7.1)图(7.2)
请写出这四个图案都具有的两个共同特征.
特征1:_________________________________________________;
特征2:_________________________________________________.
图(7.1)
典型举例(三)开放型问题
1、若等腰三角形的一个内角等于88°,则另外两个角的度数分别为(
)
A、88°、4°
B、46°、46°或88°、4°
C、46°、46°
D、88°、24°
2、若等腰三角形的一个内角等于92°,则另两个角的度数分别是(
)
A、92°、16°
B、44°、44°
C、92°、16°或44°、44°
D、46°、46°
3、等腰三角形的一边长是10,另一连长是7,则它的周长是(
)
A、27
B、24
C、17
D、27或24
4、已知等腰三角形的一边等于3,一边等于6,则它的周长是(
)
A、12
B、12或15
C、15
D、15或18
典型举例(四)方案设计类
要在河边修建一个水泵站,向张庄A、李庄B送水。修在河边什么地方,可使使用的水管最短?
·
·
A
B
a
1、下列图形中一定是轴对称图形的是(
)
A.直角三角形
B.长方形
C.任意三角形
D.有一角为60°的直角三角形
2、等腰三角形的三边长均为整数,且周长为13,
则底边是(
)
A.1或3
B.3或5
C.1或5
D.1或3或5
4、若等腰梯形的两底之差等于一腰长,
则腰与下底的夹角等于(
)
A.150
B.300
C.450
D.600
5、△ABC中,∠A=300,当∠B=
时,△ABC是等腰三角形。
6.等腰三角形的两边长分别为3cm和6cm,
则它的周长为____
1、等腰三角形一腰上的高与底边所成的角等于(
)
A.
顶角
B.
顶角的一半
C.
顶角的两倍
D.
底角的一半
2、等腰三角形两边的长分别为2cm和5cm,则这个三角形的周长是(
)
A.
9cm
B.
12cm
C.
9cm或12cm
D.
在9cm与12cm之间
3、如图,等腰△ABC中,AD⊥BC于D,已知DC=2cm,AB=3cm,则△ABC的周长为___________。
4、已知:等腰三角形的一个角是80°,则它的另外两个角是 。
A
B
C
D
B
B
10cm
50°50°或80°20°
⑴如图,在Rt△ABC中,AB=AC,∠BAC=900,P为BC的中点,
Rt△EPF
(∠
EPF=900)可绕P点转动
(点E不与A、B重合),给出下列4个结论:①AE=CF
②
△EPF是等腰直角三角形③四边形AEPF的面积等于△ABC面积的一半④EF=AP,上述结论始终正确的有(
)个.
A.1
B.2
C.3
D.4
B
A
C
P
E
F
课后提高
⑵如图,在Rt△ABC中,AB=AC,∠A=900,点D是BC上的任意一点,DF⊥AB,DE⊥AC,M为BC的中点,试判断△MEF是什么三角形,并证明你的结论.
A
B
C
D
M
E
F
自主探索
3、如图AC=BC,且AC⊥BC,D为AC上的一点,BD=2AE,AE⊥BE,求证:BE平分∠ABC.
A
B
C
E
D
复习
1、什么叫轴对称?什么叫做两个图形关于某一条直线成轴对称?什么叫轴对称图形?“轴对称图形”与“两个图形关于某一条直线成轴对称”有什么区别?
2、轴对称的基本性质是什么?如何画一个图形关于某条直线对称的图形?
3、在直角坐标系中,点P(x,y)关于x轴和y轴的对称点的坐标有什么特点?
知识点回顾
4、什么叫线段的垂直平分线?线段的垂直平分线有什么性质?它的逆命题是什么?如何用尺规作线段的垂直平分线?
过一点作已知直线的垂线?
5、角的平分线具有什么性质?它的逆命题是什么?如何做角平分线?
6、等腰三角形有哪些性质?等边三角形呢?怎样判断一个三角形是等腰三角形或等边三角形?已知哪些条件,
可以用尺规做出等腰三角形?
(2)、如果把一个图形沿某一条直线折叠后,能够与另一个图形完全重合,那么这两个图形关于这条直线成轴对称。这条直线叫做它们的对称轴。折叠后两个图形上互相重合的点叫对称点。
(1)把一个图形沿着一条直线折叠后,得到另一个与
它全等的图形,图形的这种变化叫做轴对称。这条直线叫
做对称轴。
(3)成轴对称的两个图形是全等形,但全等形不一定成轴对称。
一、图形的轴对称和轴对称图形
(4)、如果一个图形沿某一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴,对折后图形上能够重合的点叫对称点。
例题1
l
75°
γ
a
b
δ
2.29
3.20
3.44
c
β
43°
α
右图中两个三角形关于直线l成轴对称。如果三角形的部分边长(单位:厘米)和角的度数如图所示,求未知的边长和角的度数。
解:因为这两个三角形关于直线l成轴对称,它们的对应角相等,对应线段相等,所以
a=3.20厘米,b=3.44厘米,c=2.29厘米;
∠α=75°,∠γ=43°。
又因为三角形的内角和为180°,所以
∠δ=∠β=180°-75°-43°=62°
区别:轴对称图形是指一个具有特殊形状的图形,对称轴不只一条;两个图形关于某一条直线成轴对称是指两个图形的特殊形状和位置关系,对称轴只有一条。
联系:
①都有一条直线,都沿直线折叠重合;②若把轴对称图形沿对称轴分成两部分,则这两个图形关于这条直线成轴对称;若把两个关于某直线成轴对称的图形看作一个整体,则它就是一个轴对称图形。
(5)、“轴对称图形”与“两个图形关于某一条直线成轴对称”的区别与联系:
(1)成轴对称的两个图形中,对应点的连线被对称轴垂直平分,对应线段相等,对应角相等。
(2)在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
(3)点(x,
y)关于x轴对称的点的坐标为______.
(4)点(x,
y)关于y轴对称的点的坐标为______.
二、轴对称的基本性质
例2、如图,作出△BCD关于直线l的对称图形。
B′
C
C′
B
D
l
解:
如图,分别作出点B、C、D三点关于直线l的对称点B′,
C′
,D三点,
△
B′C′
D就是求作的图形。
分别连接B′C,C′D,DB′
练习、在直角坐标系中,已知△ABC的顶点分别是A(-2,1),B(1.5,-4)和C(0,3)。(1)分别写出与△ABC关于y轴成轴对称的△A'B'C'的顶点的坐标。(2)分别写出与△ABC关于x轴成轴对称的△A''B''C''的顶点的坐标。
A
B
M
N
O
(1)直线MN垂直于线段AB,并且平分线段AB,我们
把直线MN叫做线段AB的垂直平分线。
垂直并且平分一条线段的直线叫做这条线段的垂直平分线,
也叫中垂线。
(2)、线段是轴对称图形,它的一条对称轴是这条线段的垂直平分线。
线段垂直平分线的性质
三、线段垂直平分线
性质定理:线段的垂直平分线上的点,到这条线段两个端点的距离相等
线段垂直平分线的性质与判定
数学语言:
∵CD⊥AB
AE=BE(已知)
∴PA=PB(线段垂直平分线上的任意一点到
这条线段两个端点的距离相等)
判定定理
到一条线段两个端点距离相等的点,在这条线段
的垂直平分线上.
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点
距离相等的点,在这条线段的垂直平分线上).
如图:在△ABC中,已知AC=16,AB的垂直平分线交AB于点D,交AC于点E,BC=14,则△BCE的周长等于多少呢?
B
A
E
D
C
解:
∵
DE是AB的垂直平分线(已知)
∴____=______(______________)
∵AC=16(已知)
∴____________
∵BC=14(已知)
∴
△BCE的周长=______
AE
BE
线段垂直平分线上的任意一点到这条线段两个端点的距离相等
BE+CE=16
30
驶向胜利的彼岸
线段的垂直平分线的作法
已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:
用尺规作线段的垂直平分线.
1.分别以点A和B为圆心,以大于AB/2长为半径作弧,两弧交于点C和D.
A
B
C
D
2.
作直线CD.
则直线CD就是线段AB的垂直平分线.
请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.
老师提示:
因为直线CD与线段AB的交点就是AB的中点,所以我们也用这种方法作线段的中点.
探究
思考
1、如图,点C在直线上,试过点C画出直线的垂线。
2、如图,如果点C不在直线上,试和同学讨论,应采取怎样的步骤,过点C画出直线的垂线?
四、垂线的画法
作法:
(1)任取一点M,使点M和点C在直线L的两侧;
(2)以C点为圆心,以CM长为半径画弧,与直线L交于A、B两点;
(3)分别以A、B两点为圆心,以大于
长为半径画弧,两弧相交于D点;
(4)过C、D两点作直线CD。
所以,直线CD就是所求作的。
角是轴对称图形,角的平分线所在的直线是它的对称轴。
角平分线上的点,到这个角的两边的距离相等。
角的内部到角的两边距离相等的点在角的平分线上。
五、角平分线的性质与判定
等腰三角形是轴对称图形。等腰三角形的对称轴是底边的垂直平分线。
等腰三角形的顶角平分线、底边上的高、底边上的中线重合(也称三线合一)。
等腰三角形的两个底角相等。
等边三角形是轴对称图形.
等边三角形每个角的平分线和这个角的对边上的中线、
高线重合(三线合一),它们所在的直线都是等边
三角形的对称轴.等边三角形共有3条对称轴.
等边三角形的各角都相等,都等于60°
六、等腰三角形
等腰三角形的判定
有两个角相等的三角形是等腰三角形。
(简称“等角对等边”).
3个角相等的三角形是等边三角形.
有两个角等于600的三角形是等边三角形.
有一个角等于600的等腰三角形是等边三角形.
等边三角形的判定
例3.如图,△ABC和△CDE都是等边三角形,且点A,C,E在一条直线上.(1)AD=BE吗?为什么?
(2)△MNC为等边三角形吗?为什么?
A
B
C
D
E
M
N
二、【巩固练习】
1.下列图形中,轴对称图形有(
).
(A)1个
(B)2个
(C)3个
(D)4个
C
3.如图,在△ABC中,∠B=90°,∠A=36°,
AC的垂直平分线MN与AB交于点D,则∠BCD的
度数是____________.
4.已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形
ADBC的周长是
.
5.如图,以正方形ABCD的一边CD为边向形外作等
边三角形CDE,则∠AEB=
.
20cm
6.
等腰三角形ABC中,
(1)若∠A=80°,则∠B=
°;
(2)若周长为8cm,AB=3cm,则BC=
cm
三、【典型例题】
例1、
已知△ABC中,AB=AC=10,DE垂直平分AB,交
AC于E,已知三角形BEC的周长是16.
求三角形ABC的周长.
.
1、等腰三角形一边长为2,周长为8,则腰长为
.
2、
如图1,在△ABC中,AM垂直平分BC,若AB=12,BM=10,则△ABC的周长为
.
3、
如图2,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,若DE=3cm,则DF=
cm.
典型举例(一)概念直接应用类
1、有一个内角为60°的等腰三角形,腰长为6cm,那么这个三角形的周长为___________cm.
2、已知等腰三角形的一边长为6,一个外角为1200,则它的周长为(
)
A、12
B、15
C、16
D、18
3、在“线段、锐角、三角形、等边三角形、”这四个图形中,是轴对称图形的有
个,其中对称轴最多的是
。
4、在Rt△ABC中,斜边上的中线长为5cm,则斜边长为:
5、到三角形的三个顶点距离相等的点是(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
典型举例(二)折叠展开类
1、将一正方形纸片按图中(1)、(2)的方式依次对折后,再沿(3)中的虚线裁剪,最后将(4)中的纸片打开铺平,所得图案应该是下面图案中的(
)
(1)
(2)
(3)
(4)
B
A
C
D
2、认真观察图(7.1)的4个图中阴影部分构成的图案,回答下列问题:图(7.1)图(7.2)
请写出这四个图案都具有的两个共同特征.
特征1:_________________________________________________;
特征2:_________________________________________________.
图(7.1)
典型举例(三)开放型问题
1、若等腰三角形的一个内角等于88°,则另外两个角的度数分别为(
)
A、88°、4°
B、46°、46°或88°、4°
C、46°、46°
D、88°、24°
2、若等腰三角形的一个内角等于92°,则另两个角的度数分别是(
)
A、92°、16°
B、44°、44°
C、92°、16°或44°、44°
D、46°、46°
3、等腰三角形的一边长是10,另一连长是7,则它的周长是(
)
A、27
B、24
C、17
D、27或24
4、已知等腰三角形的一边等于3,一边等于6,则它的周长是(
)
A、12
B、12或15
C、15
D、15或18
典型举例(四)方案设计类
要在河边修建一个水泵站,向张庄A、李庄B送水。修在河边什么地方,可使使用的水管最短?
·
·
A
B
a
1、下列图形中一定是轴对称图形的是(
)
A.直角三角形
B.长方形
C.任意三角形
D.有一角为60°的直角三角形
2、等腰三角形的三边长均为整数,且周长为13,
则底边是(
)
A.1或3
B.3或5
C.1或5
D.1或3或5
4、若等腰梯形的两底之差等于一腰长,
则腰与下底的夹角等于(
)
A.150
B.300
C.450
D.600
5、△ABC中,∠A=300,当∠B=
时,△ABC是等腰三角形。
6.等腰三角形的两边长分别为3cm和6cm,
则它的周长为____
1、等腰三角形一腰上的高与底边所成的角等于(
)
A.
顶角
B.
顶角的一半
C.
顶角的两倍
D.
底角的一半
2、等腰三角形两边的长分别为2cm和5cm,则这个三角形的周长是(
)
A.
9cm
B.
12cm
C.
9cm或12cm
D.
在9cm与12cm之间
3、如图,等腰△ABC中,AD⊥BC于D,已知DC=2cm,AB=3cm,则△ABC的周长为___________。
4、已知:等腰三角形的一个角是80°,则它的另外两个角是 。
A
B
C
D
B
B
10cm
50°50°或80°20°
⑴如图,在Rt△ABC中,AB=AC,∠BAC=900,P为BC的中点,
Rt△EPF
(∠
EPF=900)可绕P点转动
(点E不与A、B重合),给出下列4个结论:①AE=CF
②
△EPF是等腰直角三角形③四边形AEPF的面积等于△ABC面积的一半④EF=AP,上述结论始终正确的有(
)个.
A.1
B.2
C.3
D.4
B
A
C
P
E
F
课后提高
⑵如图,在Rt△ABC中,AB=AC,∠A=900,点D是BC上的任意一点,DF⊥AB,DE⊥AC,M为BC的中点,试判断△MEF是什么三角形,并证明你的结论.
A
B
C
D
M
E
F
自主探索
3、如图AC=BC,且AC⊥BC,D为AC上的一点,BD=2AE,AE⊥BE,求证:BE平分∠ABC.
A
B
C
E
D
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
