人教版数学七年级上册4.3.3余角和补角课件(19张)
文档属性
| 名称 | 人教版数学七年级上册4.3.3余角和补角课件(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 573.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览


文档简介
余角和补角
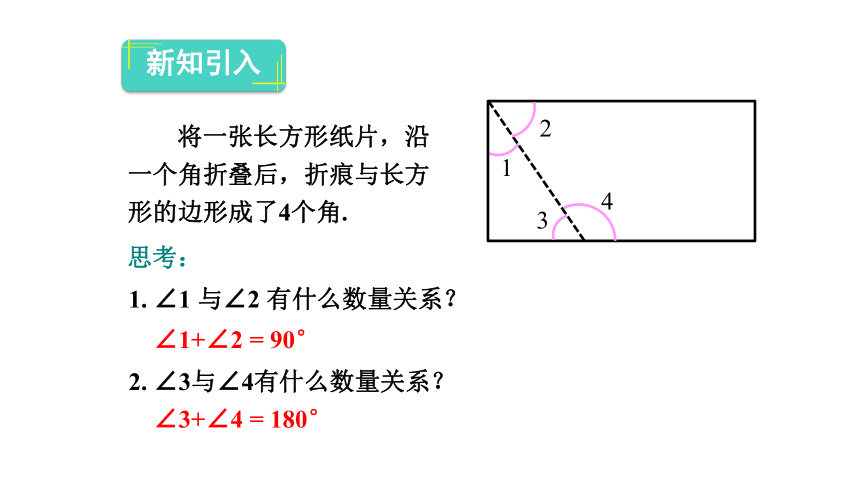
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
思考:
1. ∠1 与∠2 有什么数量关系?
∠1+∠2 = 90°
2. ∠3与∠4有什么数量关系?
∠3+∠4 = 180°
新知引入
余角和补角的概念
一
1
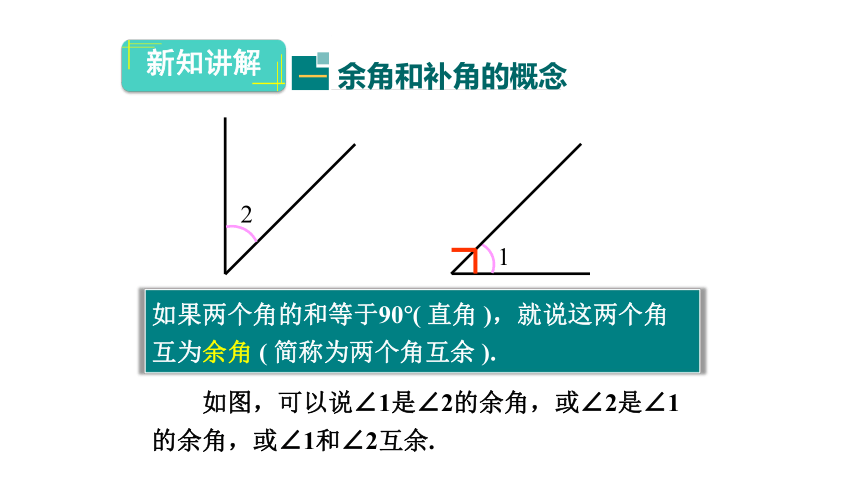
如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如图,可以说∠1是∠2的余角,或∠2是∠1的余角,或∠1和∠2互余.
2
新知讲解
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
跟踪练习
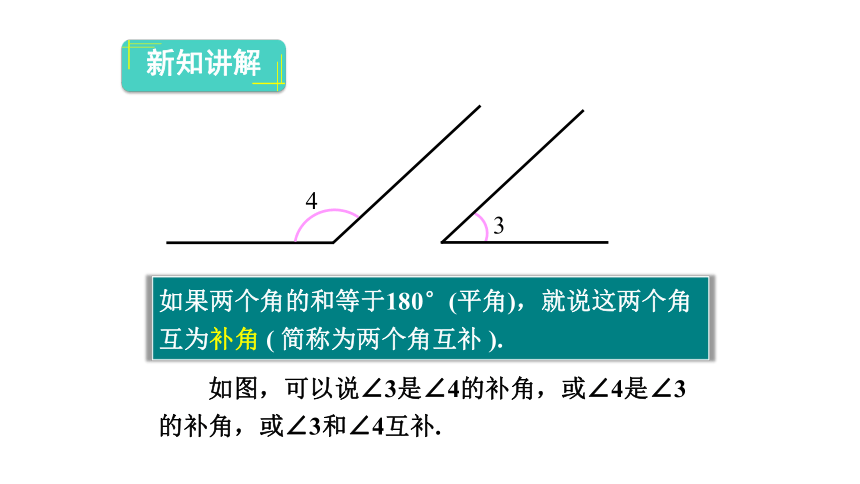
如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
如图,可以说∠3是∠4的补角,或∠4是∠3的补角,或∠3和∠4互补.
4
3
新知讲解
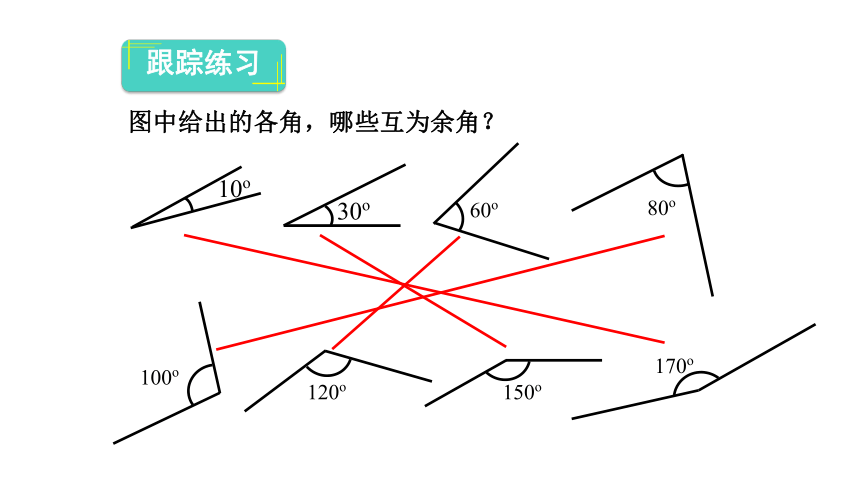
10o
30o
60o
80o
100o
120o
150o
170o
跟踪练习
图中给出的各角,哪些互为余角?
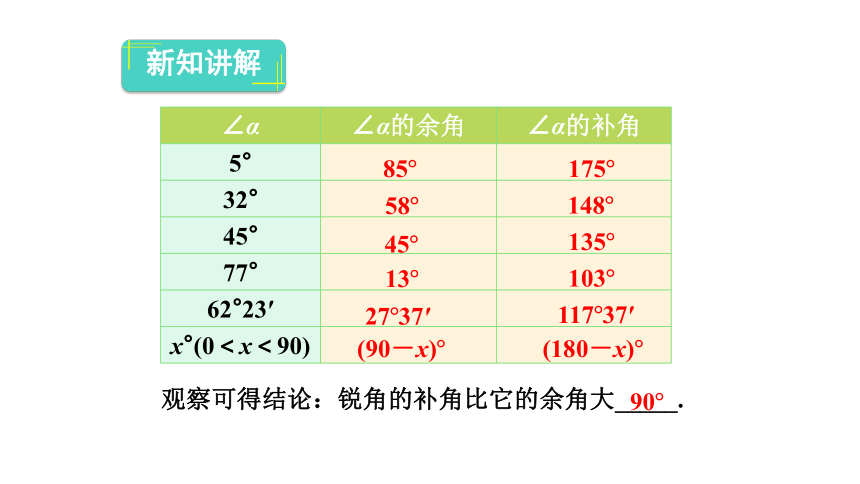
{8799B23B-EC83-4686-B30A-512413B5E67A}∠α
∠α的余角
∠α的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
(90-x)°
(180-x)°
观察可得结论:锐角的补角比它的余角大_____.
90°
新知讲解
例1 若一个角的补角等于它的余角的 4 倍,求这个角的度数.
解:设这个角为 x,
则它的补角是 (180°-x) ,余角是 (90°-x).
根据题意,得
180°-x = 4 (90°-x) .
解得 x = 60°.
答:这个角的度数是 60°.
新知应用
例2 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
解:设∠AOB=x,
因为∠AOC与∠AOB互补,
则∠AOC=180°-x.
因为OM,ON分别为∠AOC,
∠AOB的平分线,
?
新知应用
O
D
A
B
C
N
M
?
解得x=50°,则180°-x=130°.
即∠AOB=50°,∠AOC=130°.
新知应用
例2 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
O
D
A
B
C
N
M
∠1 与∠2,∠3都互为补角,
∠2 与∠3 的大小有什么关系?
余角和补角的性质
二
思考:
1
2
同角 (等角) 的补角相等.
结论:
3
∠2=180°-∠1
∠3=180°-∠1
同角 (等角) 的余角相等.
类似地,可以得到:
=
新知讲解
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线 OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线 OB
射线 OC
射线 OD
射线 OE
射线 OF
射线 OH
射线 OG
新知讲解
方位角
三
45°
如图,说出下列方位:
(1) 射线 OA 表示的方向
为 .
(2) 射线 OB 表示的方向
为 .
(3) 射线 OC 表示的方向
为 .
(4) 射线 OD 表示的方向
为 .
北
东
西
南
C
A
B
D
北偏东 40°
北偏西 65°
南偏西 45°(西南)
南偏东 20°
40°
65°
70°
O
20°
跟踪练习
解:因为点A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
O
A
B
C
D
E
?
新知应用
例1 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
新知应用
O
A
B
C
D
E
例1 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
例2 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上
又分别发现了客轮B,
货轮C和海岛D. 仿照
表示灯塔方位的方法
画出表示客轮B,货
轮C和海岛D方向的射线.
东
南
西
北
60°
● B
40°
10°
45°
C ●
● A
● D
O
●
新知应用
{ED083AE6-46FA-4A59-8FB0-9F97EB10719F}
互余
互补
两角间的数量关系
对应图形
性质
同角或等角的
补角相等
同角或等角的
余角相等
课堂总结
方位角
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向.
定义
书写
通常要先写北或南,再写偏东或偏西.
课堂总结
谢谢聆听
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
思考:
1. ∠1 与∠2 有什么数量关系?
∠1+∠2 = 90°
2. ∠3与∠4有什么数量关系?
∠3+∠4 = 180°
新知引入
余角和补角的概念
一
1
如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如图,可以说∠1是∠2的余角,或∠2是∠1的余角,或∠1和∠2互余.
2
新知讲解
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
跟踪练习
如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
如图,可以说∠3是∠4的补角,或∠4是∠3的补角,或∠3和∠4互补.
4
3
新知讲解
10o
30o
60o
80o
100o
120o
150o
170o
跟踪练习
图中给出的各角,哪些互为余角?
{8799B23B-EC83-4686-B30A-512413B5E67A}∠α
∠α的余角
∠α的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
(90-x)°
(180-x)°
观察可得结论:锐角的补角比它的余角大_____.
90°
新知讲解
例1 若一个角的补角等于它的余角的 4 倍,求这个角的度数.
解:设这个角为 x,
则它的补角是 (180°-x) ,余角是 (90°-x).
根据题意,得
180°-x = 4 (90°-x) .
解得 x = 60°.
答:这个角的度数是 60°.
新知应用
例2 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
解:设∠AOB=x,
因为∠AOC与∠AOB互补,
则∠AOC=180°-x.
因为OM,ON分别为∠AOC,
∠AOB的平分线,
?
新知应用
O
D
A
B
C
N
M
?
解得x=50°,则180°-x=130°.
即∠AOB=50°,∠AOC=130°.
新知应用
例2 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
O
D
A
B
C
N
M
∠1 与∠2,∠3都互为补角,
∠2 与∠3 的大小有什么关系?
余角和补角的性质
二
思考:
1
2
同角 (等角) 的补角相等.
结论:
3
∠2=180°-∠1
∠3=180°-∠1
同角 (等角) 的余角相等.
类似地,可以得到:
=
新知讲解
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线 OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线 OB
射线 OC
射线 OD
射线 OE
射线 OF
射线 OH
射线 OG
新知讲解
方位角
三
45°
如图,说出下列方位:
(1) 射线 OA 表示的方向
为 .
(2) 射线 OB 表示的方向
为 .
(3) 射线 OC 表示的方向
为 .
(4) 射线 OD 表示的方向
为 .
北
东
西
南
C
A
B
D
北偏东 40°
北偏西 65°
南偏西 45°(西南)
南偏东 20°
40°
65°
70°
O
20°
跟踪练习
解:因为点A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
O
A
B
C
D
E
?
新知应用
例1 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
新知应用
O
A
B
C
D
E
例1 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
例2 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上
又分别发现了客轮B,
货轮C和海岛D. 仿照
表示灯塔方位的方法
画出表示客轮B,货
轮C和海岛D方向的射线.
东
南
西
北
60°
● B
40°
10°
45°
C ●
● A
● D
O
●
新知应用
{ED083AE6-46FA-4A59-8FB0-9F97EB10719F}
互余
互补
两角间的数量关系
对应图形
性质
同角或等角的
补角相等
同角或等角的
余角相等
课堂总结
方位角
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向.
定义
书写
通常要先写北或南,再写偏东或偏西.
课堂总结
谢谢聆听
