【A典学案】1.4 三角函数的计算 课件(18张PPT)
文档属性
| 名称 | 【A典学案】1.4 三角函数的计算 课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览








文档简介
第一章 直角三角形的边角关系
第4课时 三角函数的计算
北师大版 九年级下册
温故知新
1.计算:
2.在△ABC 中,∠C=90°,已知 BC=3,AC= ,
则 sin A=_______,∠A=_______;cos B=_______,∠B=_______.
3.在△ABC 中,∠C=90°,已知 AB=4,AC=
则 tan A=_______,∠A=_________
4. 若 sinA= , 则 ∠A=________;
若 cos B= , 则 ∠B=________;
若 tan A= , 则 ∠A=___________.
阅读感知
阅读课本 12~14 页的内容,完成下面的填空:
1.用科学计算器求三角函数值:
计算整数度数的锐角三角函数值的方法:先按三角函数键,然后由高位到地位按表示度数的整数,再按=键,屏幕显示结果
阅读感知
2.求 sin 72°38′25′′,按键顺序为:
所以 sin 72°38′25′′=_______________.
计算非整数度数的锐角三角函数值的方法:先按三角函数键,再按“度 DMS”、“分 DMS”、“秒DMS”,最后按“=”键,屏幕显示结果.
阅读感知
3.已知三角函数值,用计算器求角度,要用到 sin,cos,tan 的第二功能“_________,_________,_________和_________键”.
(1)已知 sinA=0.981 6,求∠A.其按键顺序为:
显示结果为
(2)已知 cosA=0.860 7,求∠A.其按键顺序为:
显示结果为
(3)已知 tan A=56.78,求∠A.
其按键顺序为:___________________________________
阅读感知
具体操作步骤是:先按__________键,再按 之一,再依次按三角函数值,最后按__________键, 则屏幕上就会显示出结果.
上述按键方法显示的结果是以________为单位的,再按 键即可显示以__________为单位的结果.由于所显示的度数中“秒”的情形有两位小数,通常应将其四舍五入到个位.
显示结果为 =88.991 020 49.
合作探究
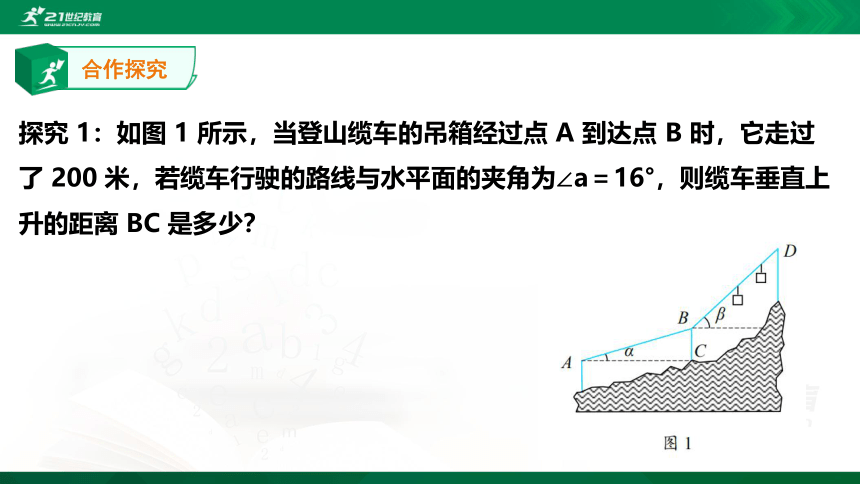
探究 1:如图 1 所示,当登山缆车的吊箱经过点 A 到达点 B 时,它走过了 200 米,若缆车行驶的路线与水平面的夹角为∠a=16°,则缆车垂直上升的距离 BC 是多少?
合作探究
探究 2:在探究 1 中,当缆车继续由点 B 到达点 D 时,它又走了 200 米,缆车由点 B 到点 D 的行驶路线与水平面的夹角为∠β=42°,由此你还能计算什么?
合作探究
探究 3:如图 2 所示,在 Rt△ABC 中,∠C=90°,AC=2,BC=4.求∠A,∠B 的度数.(精确到 1″)解 :∵tanA=_________,
由计算器求得∠A≈_______,
∴∠B≈________.
思考:观察上面求角的方法,你能否找到其他的方法?在直角三角形中,知道任意两边你能否求出两个锐角的度数?
典例精讲
类型之一 利用计算器求任意锐角的三角函数值
【例 1】用计算器求下列各式的值:
(1)cos 63°17′; (2)tan 27.35°; (3)sin 39°57′6″.
解析:(1)0.4496;
(2)0.5172;
(3)0.6421.
典例精讲
类型之二 已知锐角的三角函数值,求相应的锐角
【例 2】已知下列锐角三角函数值,用计算器求其相应的锐角;
(1)sin A=0.732 5,sin B=0.054 7;
(2)cos A=0.605 4,cos B=0.165 9;
(3)tan A=4.842 5,tan B=0.881 6.
解析:(1)A=47°5′47″,B=3°8′8″;
(2)A=52°44′33″,B=80°27′12″;
(3)A=78°19′56″,B=41°23′58″.
典例精讲
类型之三 锐角三角函数在实际生活中的应用
【例 3】某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手 AB 及两根与 FG 垂直且长为 1 米的不锈钢架杆 AD 和 BC(杆子的底端分别为 D,C)且∠DAB=66.5°.
(1)求点 D 与点 C 的高度差 DH;
(2)求所用不锈钢材料的总长度 l(即 AD+AB+BC,结果精确到 0.1 米,参考数据:sin 66.5°≈0.92,cos 66.5°≈0.40,tan 66.5°≈2.30).
典例精讲
解析:
(2)过B作BM⊥AH于M,
则四边形BCHM是矩形.∴MH=BC=1,
∴AM=AH-MH=1+1.2-1=1.2(米),
在Rt△AMB中,∠A=66.5°,
∴AB= ≈3.0(米),
∴l=AD+AB+BC≈1+3.0+1=5.0(米).
答:所用不锈钢材料的总长度约为5.0米
课堂操练
1.用计算器求 tan 26°,cos 27°,sin 28°的值,它们的大小关系是
( )
A.tan 26°<cos 27°<sin 28° B.tan 26°<sin 28°<cos 27°
C.sin 28°<tan 26°<cos 27° D.cos 27°<sin 28°<tan 26° 2.用2.计算器求 sin 56°,cos 20°,tan 47°的值,它们的大小关系为( )
A.sin 56°<cos 20°<tan 47° B.cos 20°<sin 56°<tan 47°
C.cos 20°<tan 47°<sin 56° D.tan 47°<sin 56°<cos 20°
C
A
课堂操练
3.已知 α 为锐角,若 cos α=0.432 1,则锐角 α 的范围在特殊锐角 _____________之间.
4.用计算器求下列各式的值(保留四个有效数字):
(1)sin 59°; (2)cos 68°42′; (3)tan 75°.
60°~90°
解析:(1)0.857 2;
(2)0.363 3;
(3)3.732
课堂操练
5.如图所示,为了农田灌溉的需要,某地区利用一土堤修筑一条水渠,在堤中间挖出深为 1.5 m,下底宽AB=2.2 m,坡度为 1︰0.8 的渠道(其横断面为等腰梯形),求∠BAD 及∠ADE 的度数.(精确到 1°)
解析:连接DC,过A作AG⊥DC于G,AG=1.5 m,
坡度
在Rt△ADG中,
∠GAD=38°39′,
∴∠DAB=∠ADE=128°39′≈129°.
中考在线
(吉林)墙壁及淋浴花洒截面如图所示.已知花洒底座 A 与地面的距离 AB 为 170 cm,花洒 AC 的长为 30 cm,与墙壁的夹角∠CAD 为 43°.求花洒顶端 C 到地面的距离 CE.(结果精确到 1 cm,参考数据:sin 43°=0.68,cos 43°=0.73,tan 43°=0.93)
中考在线
解析:过C作CF⊥AB于F,则∠AFC=90°,
在Rt△ACF中,AC=30,∠CAF=43°,
∵cos∠CAF= ,
∴AF=AC·cos∠CAF=30×0.73=21.9,
∴CE=BF=AB+AF=170+21.9=191.9≈192,
答:花洒顶端C到地面的距离CE为192 cm
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第4课时 三角函数的计算
北师大版 九年级下册
温故知新
1.计算:
2.在△ABC 中,∠C=90°,已知 BC=3,AC= ,
则 sin A=_______,∠A=_______;cos B=_______,∠B=_______.
3.在△ABC 中,∠C=90°,已知 AB=4,AC=
则 tan A=_______,∠A=_________
4. 若 sinA= , 则 ∠A=________;
若 cos B= , 则 ∠B=________;
若 tan A= , 则 ∠A=___________.
阅读感知
阅读课本 12~14 页的内容,完成下面的填空:
1.用科学计算器求三角函数值:
计算整数度数的锐角三角函数值的方法:先按三角函数键,然后由高位到地位按表示度数的整数,再按=键,屏幕显示结果
阅读感知
2.求 sin 72°38′25′′,按键顺序为:
所以 sin 72°38′25′′=_______________.
计算非整数度数的锐角三角函数值的方法:先按三角函数键,再按“度 DMS”、“分 DMS”、“秒DMS”,最后按“=”键,屏幕显示结果.
阅读感知
3.已知三角函数值,用计算器求角度,要用到 sin,cos,tan 的第二功能“_________,_________,_________和_________键”.
(1)已知 sinA=0.981 6,求∠A.其按键顺序为:
显示结果为
(2)已知 cosA=0.860 7,求∠A.其按键顺序为:
显示结果为
(3)已知 tan A=56.78,求∠A.
其按键顺序为:___________________________________
阅读感知
具体操作步骤是:先按__________键,再按 之一,再依次按三角函数值,最后按__________键, 则屏幕上就会显示出结果.
上述按键方法显示的结果是以________为单位的,再按 键即可显示以__________为单位的结果.由于所显示的度数中“秒”的情形有两位小数,通常应将其四舍五入到个位.
显示结果为 =88.991 020 49.
合作探究
探究 1:如图 1 所示,当登山缆车的吊箱经过点 A 到达点 B 时,它走过了 200 米,若缆车行驶的路线与水平面的夹角为∠a=16°,则缆车垂直上升的距离 BC 是多少?
合作探究
探究 2:在探究 1 中,当缆车继续由点 B 到达点 D 时,它又走了 200 米,缆车由点 B 到点 D 的行驶路线与水平面的夹角为∠β=42°,由此你还能计算什么?
合作探究
探究 3:如图 2 所示,在 Rt△ABC 中,∠C=90°,AC=2,BC=4.求∠A,∠B 的度数.(精确到 1″)解 :∵tanA=_________,
由计算器求得∠A≈_______,
∴∠B≈________.
思考:观察上面求角的方法,你能否找到其他的方法?在直角三角形中,知道任意两边你能否求出两个锐角的度数?
典例精讲
类型之一 利用计算器求任意锐角的三角函数值
【例 1】用计算器求下列各式的值:
(1)cos 63°17′; (2)tan 27.35°; (3)sin 39°57′6″.
解析:(1)0.4496;
(2)0.5172;
(3)0.6421.
典例精讲
类型之二 已知锐角的三角函数值,求相应的锐角
【例 2】已知下列锐角三角函数值,用计算器求其相应的锐角;
(1)sin A=0.732 5,sin B=0.054 7;
(2)cos A=0.605 4,cos B=0.165 9;
(3)tan A=4.842 5,tan B=0.881 6.
解析:(1)A=47°5′47″,B=3°8′8″;
(2)A=52°44′33″,B=80°27′12″;
(3)A=78°19′56″,B=41°23′58″.
典例精讲
类型之三 锐角三角函数在实际生活中的应用
【例 3】某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手 AB 及两根与 FG 垂直且长为 1 米的不锈钢架杆 AD 和 BC(杆子的底端分别为 D,C)且∠DAB=66.5°.
(1)求点 D 与点 C 的高度差 DH;
(2)求所用不锈钢材料的总长度 l(即 AD+AB+BC,结果精确到 0.1 米,参考数据:sin 66.5°≈0.92,cos 66.5°≈0.40,tan 66.5°≈2.30).
典例精讲
解析:
(2)过B作BM⊥AH于M,
则四边形BCHM是矩形.∴MH=BC=1,
∴AM=AH-MH=1+1.2-1=1.2(米),
在Rt△AMB中,∠A=66.5°,
∴AB= ≈3.0(米),
∴l=AD+AB+BC≈1+3.0+1=5.0(米).
答:所用不锈钢材料的总长度约为5.0米
课堂操练
1.用计算器求 tan 26°,cos 27°,sin 28°的值,它们的大小关系是
( )
A.tan 26°<cos 27°<sin 28° B.tan 26°<sin 28°<cos 27°
C.sin 28°<tan 26°<cos 27° D.cos 27°<sin 28°<tan 26° 2.用2.计算器求 sin 56°,cos 20°,tan 47°的值,它们的大小关系为( )
A.sin 56°<cos 20°<tan 47° B.cos 20°<sin 56°<tan 47°
C.cos 20°<tan 47°<sin 56° D.tan 47°<sin 56°<cos 20°
C
A
课堂操练
3.已知 α 为锐角,若 cos α=0.432 1,则锐角 α 的范围在特殊锐角 _____________之间.
4.用计算器求下列各式的值(保留四个有效数字):
(1)sin 59°; (2)cos 68°42′; (3)tan 75°.
60°~90°
解析:(1)0.857 2;
(2)0.363 3;
(3)3.732
课堂操练
5.如图所示,为了农田灌溉的需要,某地区利用一土堤修筑一条水渠,在堤中间挖出深为 1.5 m,下底宽AB=2.2 m,坡度为 1︰0.8 的渠道(其横断面为等腰梯形),求∠BAD 及∠ADE 的度数.(精确到 1°)
解析:连接DC,过A作AG⊥DC于G,AG=1.5 m,
坡度
在Rt△ADG中,
∠GAD=38°39′,
∴∠DAB=∠ADE=128°39′≈129°.
中考在线
(吉林)墙壁及淋浴花洒截面如图所示.已知花洒底座 A 与地面的距离 AB 为 170 cm,花洒 AC 的长为 30 cm,与墙壁的夹角∠CAD 为 43°.求花洒顶端 C 到地面的距离 CE.(结果精确到 1 cm,参考数据:sin 43°=0.68,cos 43°=0.73,tan 43°=0.93)
中考在线
解析:过C作CF⊥AB于F,则∠AFC=90°,
在Rt△ACF中,AC=30,∠CAF=43°,
∵cos∠CAF= ,
∴AF=AC·cos∠CAF=30×0.73=21.9,
∴CE=BF=AB+AF=170+21.9=191.9≈192,
答:花洒顶端C到地面的距离CE为192 cm
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
