【A典学案】1.5 解直角三角形 课件(16张PPT)
文档属性
| 名称 | 【A典学案】1.5 解直角三角形 课件(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览





文档简介
第一章 直角三角形的边角关系
第5课时 解直角三角形
北师大版 九年级下册
温故知新
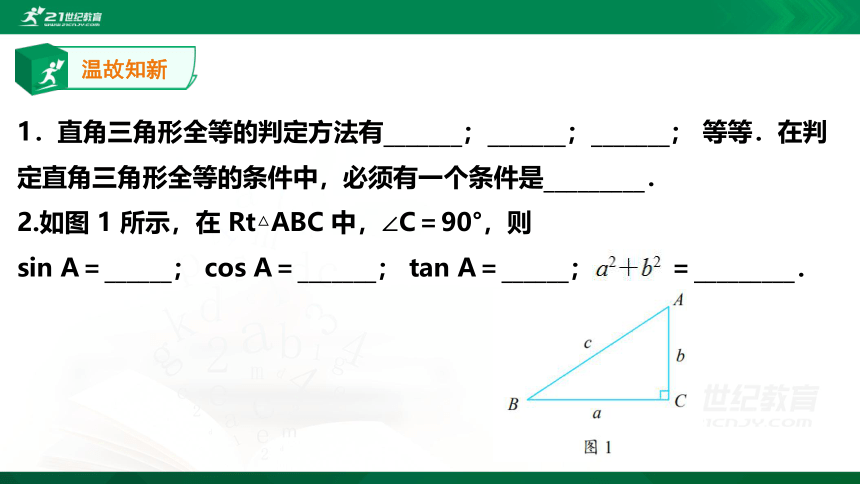
1.直角三角形全等的判定方法有_______;_______;_______; 等等.在判定直角三角形全等的条件中,必须有一个条件是_________.
2.如图 1 所示,在 Rt△ABC 中,∠C=90°,则
sin A=______; cos A=_______; tan A=______; =_________.
阅读感知
阅读课本 16~17 页的内容,思考并回答下列问题:
1.在直角三角形中,除直角外,还有几个角和边?
2.由直角三角形中已知的元素,求出所有未知元素的过程,叫做________.
阅读感知
3.在 Rt△ABC 中,∠C 为直角,∠A,∠B,∠C 所对的边分别为 a,b,c,那么 a,b,c,∠A,∠B 这五个元素间有哪些等量关系呢?
(1) 两 锐 角 之 间 的 关 系 :_________;
(2)三边之间的关系:___________________(勾股定理);
(3)边角之间的关系:sin A= _____;cos A=_____;tan A= _____;
sin B= _____;cos B=_____;tan B=_____.
阅读感知
4.我们已掌握 Rt△ABC 的边角关系、三边关系、角角关系,这些关系,在知道其中的 个元素(至少一个是边)后,就可以求出其余的 个未知元素.为什么两个已知元素中必须有一条边呢?
合作探究
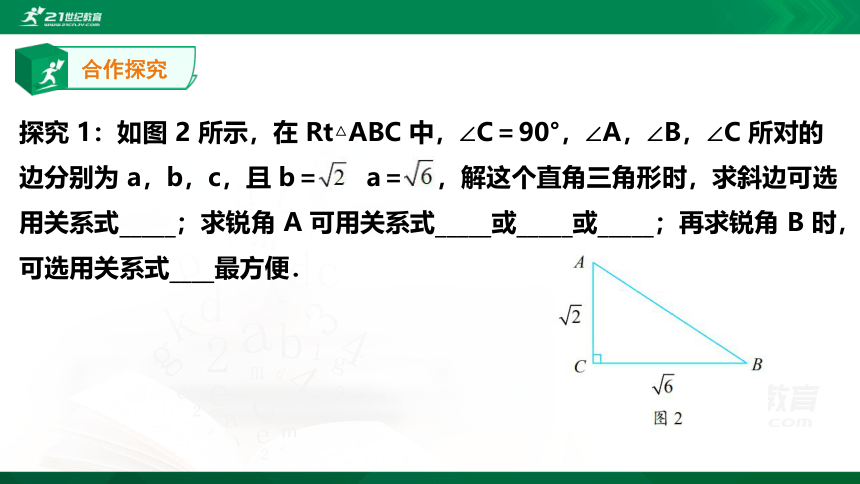
探究 1:如图 2 所示,在 Rt△ABC 中,∠C=90°,∠A,∠B,∠C 所对的边分别为 a,b,c,且 b= ,a= ,解这个直角三角形时,求斜边可选用关系式_____;求锐角 A 可用关系式_____或_____或_____;再求锐角 B 时,可选用关系式____最方便.
合作探究
探究 2:在上题中,若不先用勾股定理求斜边 c,你会解这个直角三角形吗?
合作探究
探究 3:如图 3,在 Rt△ABC 中,∠C 为直角,∠A,∠B,∠C 所对的边分别为 a,b,c,且 b=20,∠B=35°,你能用不同的方法解这个直角三角形吗?(结果保留小数点后一位)
合作探究
探究 4:总结你解直角三角形的方法,选择适当的式子,填写下表(以 Rt△ABC 为例,∠C=90°,∠A,∠B,∠C 所对的边分别为 a,b,c,表中“√”表示已知)
典例精讲
类型之一 可解直角三角形的解法
【例 1】在 Rt△ABC 中,∠C=90°,b=20.49,a=104.0,解这个直角三角形.
解析:
查表得∠A=78°51′.
∠B=90°-∠A=90°-78°51′=11°9.
典例精讲
类型之二 不可解直角三角形的解法
【例 2】如图所示,在 Rt△ABC 中,∠C=90°,D 为 BC 边上一点,∠DAC=30°,BD=2,AB= ,则 AC 的长是( )
分析:本例中涉及两个直角三角形,但都不是可解直角三角形,若设 CD=x,所以 tan∠DAC= ,故 AC=x,在 Rt△ABC 中,利用勾股定理,可建构关于 x 的方程 ,解得 x的值,从而求得 AC 的值.
A
课堂操练
1.在 Rt△ABC 中,∠C=90°, ,那么 BC 的值为( )
A.2 B.4 C. D.6
2.在 Rt△ABC 中,∠C=90°,∠B=35°,AB=7,则 BC 的长为( )
A.7 sin 35° B. C.7 cos 35° D.7 tan 35°
3.在△ABC 中,∠C=90°,BC=6 cm,cos A= ,则 AB 的长是_____cm
4.如图所示,在菱形 ABCD 中,DE⊥AB,垂足为 E,DE=6 cm,sin A= ,则菱形 ABCD 的面积是_______ .
A
C
10
60
课堂操练
5.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3 m.已知木箱高 BE= ,斜面坡脚为30°,求木箱端点 E 距地面 AC 的高度 EF.
解析:连接AE,在Rt△ABE中,已知AB=3,BE= ,
∴AE=
又∵tan∠EAB= ,∴∠EAB=30°.
在Rt△AEF中,EAF=∠EAB+∠EAC=60°,
∴EF=AE·sin∠EAF= .
答:木箱端点E距地面AC的高度是3 m.
中考在线
(梧州)如图所示,在 Rt△ABC 中,∠C=90°,D 为 BC 上一点,AB=5,BD=1,tan B= .
(1)求 AD 的长;
(2)求 sin α 的值.
中考在线
解析:(1)∵tanB= ,可设AC=3x,得BC=4x,
, ,
解得x=-1(舍去),或x=1,
∴AC=3,BC=4,
中考在线
(2)过点作DE⊥AB于点E,
∵tanB= ,可设DE=3y,
则BE=4y,
解得,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第5课时 解直角三角形
北师大版 九年级下册
温故知新
1.直角三角形全等的判定方法有_______;_______;_______; 等等.在判定直角三角形全等的条件中,必须有一个条件是_________.
2.如图 1 所示,在 Rt△ABC 中,∠C=90°,则
sin A=______; cos A=_______; tan A=______; =_________.
阅读感知
阅读课本 16~17 页的内容,思考并回答下列问题:
1.在直角三角形中,除直角外,还有几个角和边?
2.由直角三角形中已知的元素,求出所有未知元素的过程,叫做________.
阅读感知
3.在 Rt△ABC 中,∠C 为直角,∠A,∠B,∠C 所对的边分别为 a,b,c,那么 a,b,c,∠A,∠B 这五个元素间有哪些等量关系呢?
(1) 两 锐 角 之 间 的 关 系 :_________;
(2)三边之间的关系:___________________(勾股定理);
(3)边角之间的关系:sin A= _____;cos A=_____;tan A= _____;
sin B= _____;cos B=_____;tan B=_____.
阅读感知
4.我们已掌握 Rt△ABC 的边角关系、三边关系、角角关系,这些关系,在知道其中的 个元素(至少一个是边)后,就可以求出其余的 个未知元素.为什么两个已知元素中必须有一条边呢?
合作探究
探究 1:如图 2 所示,在 Rt△ABC 中,∠C=90°,∠A,∠B,∠C 所对的边分别为 a,b,c,且 b= ,a= ,解这个直角三角形时,求斜边可选用关系式_____;求锐角 A 可用关系式_____或_____或_____;再求锐角 B 时,可选用关系式____最方便.
合作探究
探究 2:在上题中,若不先用勾股定理求斜边 c,你会解这个直角三角形吗?
合作探究
探究 3:如图 3,在 Rt△ABC 中,∠C 为直角,∠A,∠B,∠C 所对的边分别为 a,b,c,且 b=20,∠B=35°,你能用不同的方法解这个直角三角形吗?(结果保留小数点后一位)
合作探究
探究 4:总结你解直角三角形的方法,选择适当的式子,填写下表(以 Rt△ABC 为例,∠C=90°,∠A,∠B,∠C 所对的边分别为 a,b,c,表中“√”表示已知)
典例精讲
类型之一 可解直角三角形的解法
【例 1】在 Rt△ABC 中,∠C=90°,b=20.49,a=104.0,解这个直角三角形.
解析:
查表得∠A=78°51′.
∠B=90°-∠A=90°-78°51′=11°9.
典例精讲
类型之二 不可解直角三角形的解法
【例 2】如图所示,在 Rt△ABC 中,∠C=90°,D 为 BC 边上一点,∠DAC=30°,BD=2,AB= ,则 AC 的长是( )
分析:本例中涉及两个直角三角形,但都不是可解直角三角形,若设 CD=x,所以 tan∠DAC= ,故 AC=x,在 Rt△ABC 中,利用勾股定理,可建构关于 x 的方程 ,解得 x的值,从而求得 AC 的值.
A
课堂操练
1.在 Rt△ABC 中,∠C=90°, ,那么 BC 的值为( )
A.2 B.4 C. D.6
2.在 Rt△ABC 中,∠C=90°,∠B=35°,AB=7,则 BC 的长为( )
A.7 sin 35° B. C.7 cos 35° D.7 tan 35°
3.在△ABC 中,∠C=90°,BC=6 cm,cos A= ,则 AB 的长是_____cm
4.如图所示,在菱形 ABCD 中,DE⊥AB,垂足为 E,DE=6 cm,sin A= ,则菱形 ABCD 的面积是_______ .
A
C
10
60
课堂操练
5.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3 m.已知木箱高 BE= ,斜面坡脚为30°,求木箱端点 E 距地面 AC 的高度 EF.
解析:连接AE,在Rt△ABE中,已知AB=3,BE= ,
∴AE=
又∵tan∠EAB= ,∴∠EAB=30°.
在Rt△AEF中,EAF=∠EAB+∠EAC=60°,
∴EF=AE·sin∠EAF= .
答:木箱端点E距地面AC的高度是3 m.
中考在线
(梧州)如图所示,在 Rt△ABC 中,∠C=90°,D 为 BC 上一点,AB=5,BD=1,tan B= .
(1)求 AD 的长;
(2)求 sin α 的值.
中考在线
解析:(1)∵tanB= ,可设AC=3x,得BC=4x,
, ,
解得x=-1(舍去),或x=1,
∴AC=3,BC=4,
中考在线
(2)过点作DE⊥AB于点E,
∵tanB= ,可设DE=3y,
则BE=4y,
解得,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
