【A典学案】1.7 利用三角函数测高 课件(19张PPT)
文档属性
| 名称 | 【A典学案】1.7 利用三角函数测高 课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 16:44:34 | ||
图片预览







文档简介
第一章 直角三角形的边角关系
第7课时 利用三角函数测高
北师大版 九年级下册
温故知新
1.在 Rt△ABC 中,∠C=90°,已知 a 和∠A,则∠B=____,b=___,c=_____ .
2.在 Rt△ABC 中,∠C=90°,已知 c 和∠B,则∠A=____,a=____,b=_____ .
阅读感知
阅读课本 22~23页的内容,完成下面的填空:
1.活动课题:利用直角三角形的边角关系测量物体的高度.
活动方式:分组活动,全班交流研讨.
活动工具:___________、__________等测量工具.
阅读感知
2.活动一:测量倾斜角
测量倾斜角可以用 .
如图 1 所示,简单的测倾器由 ______、_______和支杆组成.
使用测倾器倾斜角的步骤如下:
(1)把支杆______插入地面,使支杆的中心线、铅垂线和度盘的______ 重合,这时度盘的顶线 PQ 在_______位置.
(2)转到度盘,使度盘的______对准目标 M,记下此时铅垂线所指的度数.根据测量数据,即可求出目标 M 的仰角或俯角.其理由是_________.
阅读感知
3.活动二、测量底部可以到达的物体的高度
所谓底部可以到达,就是在地面上可以无障碍地直接测得____与____之间的距离. 测量工具:测倾器(或测角仪等)、 _______.
测量步骤:如图 2 所示,要测量物体 MN 的高度,可按下步骤进行:
(1)在测量点 A 处安置___________,测得 M 的仰角∠MCE=α.
(2)量出______的水平距离 AN=l.
(3)量出______的高度 AC=a(即测倾器顶线成水平位置时与地面的距离).根据测量数据,即可求出物体 MN 的高度.
阅读感知
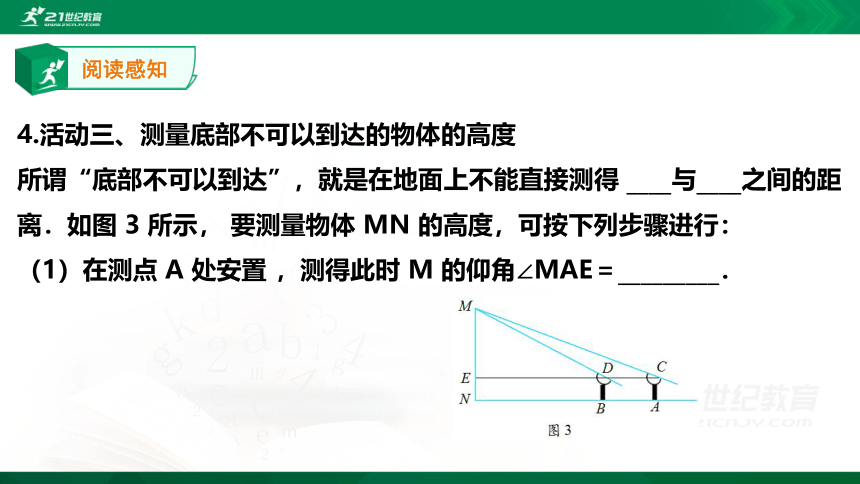
4.活动三、测量底部不可以到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得 ____与____之间的距离.如图 3 所示, 要测量物体 MN 的高度,可按下列步骤进行:
(1)在测点 A 处安置 ,测得此时 M 的仰角∠MAE=_________.
阅读感知
(2)在测点 A 与物体之间的 B 处安置_______(A,B 与 N 在一条直线上,且 A,B 之间的距离可以直接测得),测得此时 M 的仰角∠MDE=____.
(3)量出测倾器的高度 AC=BD=a,以及________之间的距离 AB=b,根据测量数据,即可求出物体MN 的高度.
合作探究
探究 1:根据活动二中的测量数据,写出求物体 MN 高度的计算过程.
合作探究
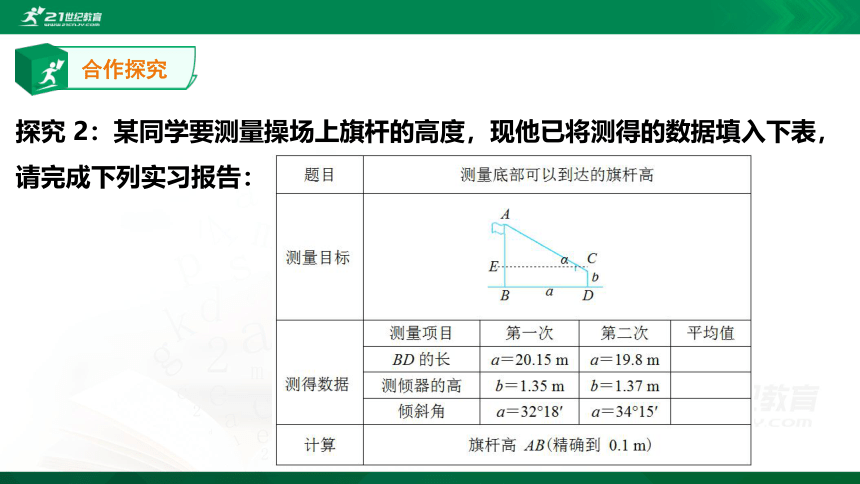
探究 2:某同学要测量操场上旗杆的高度,现他已将测得的数据填入下表,请完成下列实习报告:
合作探究
探究 3:根据活动三中的测量数据,写出求物体 MN 高度的计算过程.
典例精讲
类型之一 根据所给条件,求物体的高度
【例 1】如图所示,形状为长方形的建筑物 ABCD 的底端 BC 的长是 70 米,高 AB=30 米,从 A,C 两点可测得河对面一电视发射塔的顶端 H 的仰角分别为 30°和 60°,求塔的高度 HG.(结果精确到 1 米)
典例精讲
解析:延长AD与HG交于E,设HE=x,
在Rt△AEH中,有HE=AE·tan30°= AE.∴AE= x.
在Rt△HCG中,有HG=CG·tan 60°= CG,
∴CG= HG= (x+30).
∵CG=DE=AE-AD= x-70,
∴ (x+30)= x-70,
解得x= +15,∴HG=35 +45≈106 m.
答:HG的高约为106 m
典例精讲
类型之二 根据描述测量过程,计算物体的高度
【例 2】如图,小山上有一棵树.现有测角仪和皮尺两种测量工具,请你设计一种测量方案,在山脚水
平地面上测出小树顶端 A 到水平地面的距离 AB.要求:
(1)画出测量示意图;
(2)写出测量步骤(测量数据用字母表示);
(3)根据(2)中的数据计算 AB.
解析:此题根据题意,自己设计方案,答案不唯一
课堂操练
1.如图所示,小明用一块有一个锐角为 30°的直角三角板测量树高,已知小明离树的距离为 4 m,小明的身高为 1.6 m,那么这棵树的高度为( )
C
课堂操练
2.如图所示,在某建筑物 AC 上挂着一条宣传条幅 BC,小明站在点 F 处看条幅顶端 B,测得仰角为 45°, 再往条幅方向前进 4 m 到达点 E 处,看到条幅顶端 B,测得仰角为 59°,那么宣传条幅 BC 的长为______m.(小明的身高不计,参考数据:tan 59°= )
10
课堂操练
3.如图所示,数学实习小组在高 300 米的山腰(即 PH=300 米)P 处进行测量,测得对面山坡上 A 处的俯角为 30°,对面山脚 B 处的俯角为 60°,已知 tan∠ABC= ,点P, H,B,C ,A在同一平面上,点H,B,C在同一条直线上,且 PH⊥HC.
(1)求∠ABP 的度数;
(2)求 A,B 两点间的距离.
课堂操练
解析:(1)∵tan ∠ABC= ,∠ABC为锐角,
∴∠ABC=30°.
∵∠BPD=60°,∴∠HBP=60°,
∴∠ABP=90°.
(2)在Rt△PHB中,HP=300,∠HPB=30°,
∴PB= .
在Rt△ABP中, ,
∴AB=PB tan30°=200 =200(米).
中考在线
(泰州)某体育看台侧面的示意图如图所示,观众区 AC 的坡度 i 为 1∶2,顶端 C 离水平地面 AB 的高度为10 m,从顶棚的 D 处看 E 处的仰角 α=18°30′,竖直的立杆上 C,D 两点间的距离为 4 m,E 处到观众区底端 A 处的水平距离 AF 为 3 m.求:
(1)观众区的水平宽度 AB;
(2)顶棚的 E 处离地面的高度 EF.(sin 18°30′≈0.32,tan 18°30′≈0.33,结果精确到 0.1 m)
中考在线
解析:(1)∵观众区AC的坡度i为1∶2,顶端C离水平地面AB的高度为10 m,∴AB=2BC=20(m),
答:观众区的水平宽度AB为20 m;
(2)作CM⊥EF于M,DN⊥EF于N,则四边形MFBC,MCDN为矩形,
∴MF=BC=10,MN=CD=4,DN=MC=BF=23,
在Rt△END中,tan∠EDN= ,则EN=DN·tan∠EDN≈7.59,
∴EF=EN+MN+MF=7.59+4+10≈21.6(m),
答:顶棚的E处离地面的高度EF约为21.6 m.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第7课时 利用三角函数测高
北师大版 九年级下册
温故知新
1.在 Rt△ABC 中,∠C=90°,已知 a 和∠A,则∠B=____,b=___,c=_____ .
2.在 Rt△ABC 中,∠C=90°,已知 c 和∠B,则∠A=____,a=____,b=_____ .
阅读感知
阅读课本 22~23页的内容,完成下面的填空:
1.活动课题:利用直角三角形的边角关系测量物体的高度.
活动方式:分组活动,全班交流研讨.
活动工具:___________、__________等测量工具.
阅读感知
2.活动一:测量倾斜角
测量倾斜角可以用 .
如图 1 所示,简单的测倾器由 ______、_______和支杆组成.
使用测倾器倾斜角的步骤如下:
(1)把支杆______插入地面,使支杆的中心线、铅垂线和度盘的______ 重合,这时度盘的顶线 PQ 在_______位置.
(2)转到度盘,使度盘的______对准目标 M,记下此时铅垂线所指的度数.根据测量数据,即可求出目标 M 的仰角或俯角.其理由是_________.
阅读感知
3.活动二、测量底部可以到达的物体的高度
所谓底部可以到达,就是在地面上可以无障碍地直接测得____与____之间的距离. 测量工具:测倾器(或测角仪等)、 _______.
测量步骤:如图 2 所示,要测量物体 MN 的高度,可按下步骤进行:
(1)在测量点 A 处安置___________,测得 M 的仰角∠MCE=α.
(2)量出______的水平距离 AN=l.
(3)量出______的高度 AC=a(即测倾器顶线成水平位置时与地面的距离).根据测量数据,即可求出物体 MN 的高度.
阅读感知
4.活动三、测量底部不可以到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得 ____与____之间的距离.如图 3 所示, 要测量物体 MN 的高度,可按下列步骤进行:
(1)在测点 A 处安置 ,测得此时 M 的仰角∠MAE=_________.
阅读感知
(2)在测点 A 与物体之间的 B 处安置_______(A,B 与 N 在一条直线上,且 A,B 之间的距离可以直接测得),测得此时 M 的仰角∠MDE=____.
(3)量出测倾器的高度 AC=BD=a,以及________之间的距离 AB=b,根据测量数据,即可求出物体MN 的高度.
合作探究
探究 1:根据活动二中的测量数据,写出求物体 MN 高度的计算过程.
合作探究
探究 2:某同学要测量操场上旗杆的高度,现他已将测得的数据填入下表,请完成下列实习报告:
合作探究
探究 3:根据活动三中的测量数据,写出求物体 MN 高度的计算过程.
典例精讲
类型之一 根据所给条件,求物体的高度
【例 1】如图所示,形状为长方形的建筑物 ABCD 的底端 BC 的长是 70 米,高 AB=30 米,从 A,C 两点可测得河对面一电视发射塔的顶端 H 的仰角分别为 30°和 60°,求塔的高度 HG.(结果精确到 1 米)
典例精讲
解析:延长AD与HG交于E,设HE=x,
在Rt△AEH中,有HE=AE·tan30°= AE.∴AE= x.
在Rt△HCG中,有HG=CG·tan 60°= CG,
∴CG= HG= (x+30).
∵CG=DE=AE-AD= x-70,
∴ (x+30)= x-70,
解得x= +15,∴HG=35 +45≈106 m.
答:HG的高约为106 m
典例精讲
类型之二 根据描述测量过程,计算物体的高度
【例 2】如图,小山上有一棵树.现有测角仪和皮尺两种测量工具,请你设计一种测量方案,在山脚水
平地面上测出小树顶端 A 到水平地面的距离 AB.要求:
(1)画出测量示意图;
(2)写出测量步骤(测量数据用字母表示);
(3)根据(2)中的数据计算 AB.
解析:此题根据题意,自己设计方案,答案不唯一
课堂操练
1.如图所示,小明用一块有一个锐角为 30°的直角三角板测量树高,已知小明离树的距离为 4 m,小明的身高为 1.6 m,那么这棵树的高度为( )
C
课堂操练
2.如图所示,在某建筑物 AC 上挂着一条宣传条幅 BC,小明站在点 F 处看条幅顶端 B,测得仰角为 45°, 再往条幅方向前进 4 m 到达点 E 处,看到条幅顶端 B,测得仰角为 59°,那么宣传条幅 BC 的长为______m.(小明的身高不计,参考数据:tan 59°= )
10
课堂操练
3.如图所示,数学实习小组在高 300 米的山腰(即 PH=300 米)P 处进行测量,测得对面山坡上 A 处的俯角为 30°,对面山脚 B 处的俯角为 60°,已知 tan∠ABC= ,点P, H,B,C ,A在同一平面上,点H,B,C在同一条直线上,且 PH⊥HC.
(1)求∠ABP 的度数;
(2)求 A,B 两点间的距离.
课堂操练
解析:(1)∵tan ∠ABC= ,∠ABC为锐角,
∴∠ABC=30°.
∵∠BPD=60°,∴∠HBP=60°,
∴∠ABP=90°.
(2)在Rt△PHB中,HP=300,∠HPB=30°,
∴PB= .
在Rt△ABP中, ,
∴AB=PB tan30°=200 =200(米).
中考在线
(泰州)某体育看台侧面的示意图如图所示,观众区 AC 的坡度 i 为 1∶2,顶端 C 离水平地面 AB 的高度为10 m,从顶棚的 D 处看 E 处的仰角 α=18°30′,竖直的立杆上 C,D 两点间的距离为 4 m,E 处到观众区底端 A 处的水平距离 AF 为 3 m.求:
(1)观众区的水平宽度 AB;
(2)顶棚的 E 处离地面的高度 EF.(sin 18°30′≈0.32,tan 18°30′≈0.33,结果精确到 0.1 m)
中考在线
解析:(1)∵观众区AC的坡度i为1∶2,顶端C离水平地面AB的高度为10 m,∴AB=2BC=20(m),
答:观众区的水平宽度AB为20 m;
(2)作CM⊥EF于M,DN⊥EF于N,则四边形MFBC,MCDN为矩形,
∴MF=BC=10,MN=CD=4,DN=MC=BF=23,
在Rt△END中,tan∠EDN= ,则EN=DN·tan∠EDN≈7.59,
∴EF=EN+MN+MF=7.59+4+10≈21.6(m),
答:顶棚的E处离地面的高度EF约为21.6 m.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
