人教版 九年级数学上册 23.1 图形的旋转 同步训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学上册 23.1 图形的旋转 同步训练(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 641.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览




文档简介
人教版 九年级数学上册 23.1 图形的旋转 同步训练
一、选择题
1. 将下列图形绕其对角线的交点逆时针旋转90°,所得图形一定与原图形重合的是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
2. 如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心是 ( )
A.点A B.点B
C.点C D.点D
3. 如图,将△OAB绕点O逆时针旋转得到△OA′B′,使点B恰好落在边A′B′上.已知AB=4 cm,OB=1 cm,∠B′=60°,那么A′B的长是( )
A.4 cm B.3 cm
C.2 cm D.(4-)cm
4. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A. B.2
C.3 D.2
5. 如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB边的中点是坐标原点O,将正方形绕点C按逆时针方向旋转90°后,点B的对应点B′的坐标是( )
A.(-1,2) B.(1,4)
C.(3,2) D.(-1,0)
6. 如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )
A.(,-1) B.(1,-)
C.(2,0) D.(,0)
7. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为( )
A.4 B.2
C.6 D.2
8. 在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A顺时针旋转30°得到点A′,则点A′的坐标为( )
A.(,1) B.(,-1) C.(2,1) D.(0,2)
二、填空题
9. 如图,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过______次旋转而得到,每一次旋转______度.
10. 在平面直角坐标系中,将点A(4,2)绕原点按逆时针方向旋转90°后,其对应点A′的坐标为________.
11. 如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
12. 如图,△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 .将△BDE绕点B逆时针旋转后得△BD′E′,当点E′恰好落在线段AD′上时,CE′=________.
13. 一副三角尺如图21-K-5放置,将三角尺ADE绕点A逆时针旋转α(0°<α<90°),使得三角尺ADE的一边所在的直线与BC垂直,则α的度数为________.
图21-K-5
14. 把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为_______.
15. 分类讨论如图,点A的坐标为(-1,5),点B的坐标为(3,3),点C的坐标为(5,3),点D的坐标为(3,-1).小明发现线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_________.
教师详解详析
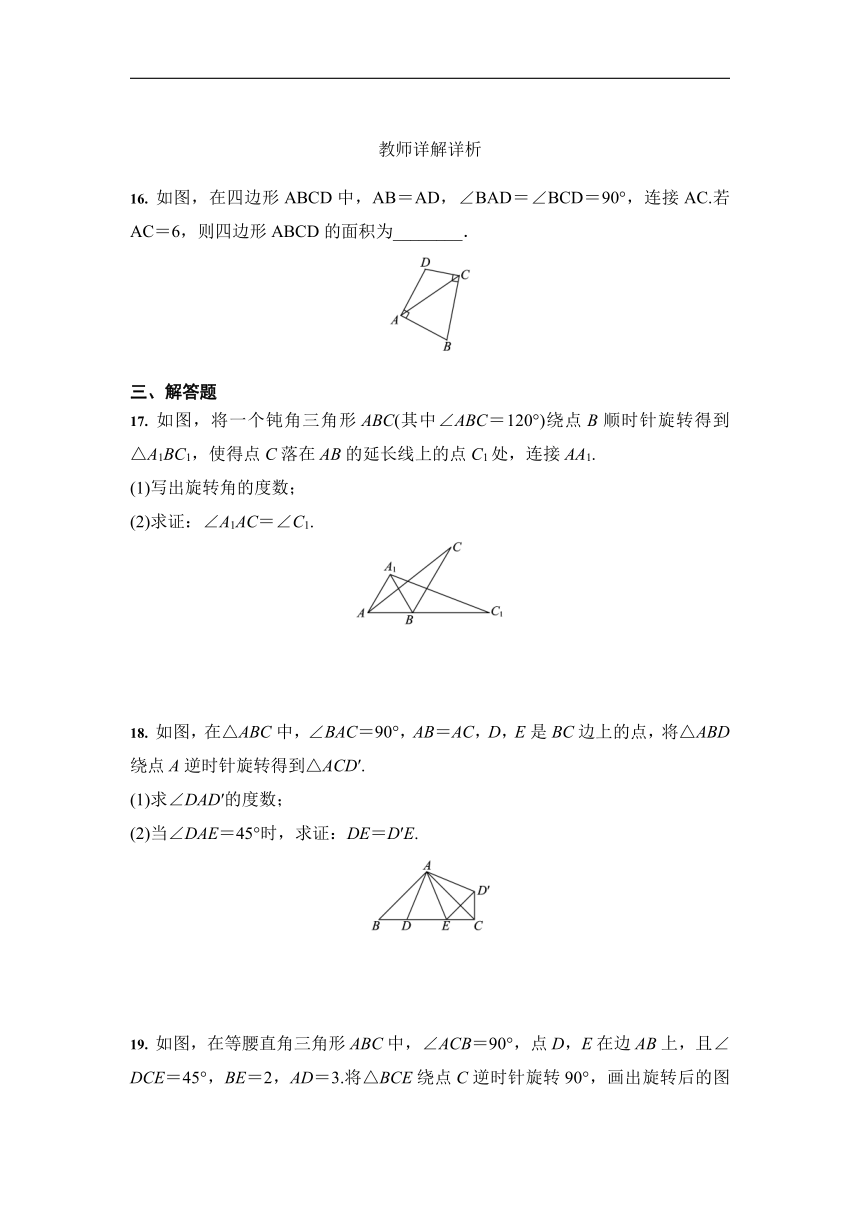
16. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
三、解答题
17. 如图,将一个钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得到△A1BC1,使得点C落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
18. 如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD′.
(1)求∠DAD′的度数;
(2)当∠DAE=45°时,求证:DE=D′E.
19. 如图,在等腰直角三角形ABC中,∠ACB=90°,点D,E在边AB上,且∠DCE=45°,BE=2,AD=3.将△BCE绕点C逆时针旋转90°,画出旋转后的图形,并求DE的长.
20. 如图,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
人教版 九年级数学上册 23.1 图形的旋转 同步训练-答案
一、选择题
1. 【答案】D [解析] 平行四边形绕其对角线的交点旋转能够与原来的图形重合的最小旋转角度数是180°,故A错误;矩形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是180°,故B错误;菱形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是180°,故C错误;正方形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是90°.故选D.
2. 【答案】B [解析] 旋转中心到对应点的距离相等.
3. 【答案】B [解析] ∵旋转前、后的两个图形是全等图形,AB=4 cm,OB=1 cm,∴A′B′=AB=4 cm,OB′=OB=1 cm.
在△OB′B中,∵∠B′=60°,OB′=OB,
∴△OB′B是等边三角形,∴BB′=OB=1 cm,
∴A′B=A′B′-BB′=4-1=3(cm).
4. 【答案】A [解析] ∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5.
∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,
∴AE=4,DE=3,∴BE=1.
在Rt△BED中,BD==.故选A.
5. 【答案】C
6. 【答案】A
7. 【答案】D [解析] 由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2 .
∵DE=2,∴在Rt△ADE中,AE==2 .故选D.
8. 【答案】A [解析] 如图,过点A作AE⊥y轴于点E,过点A′作A′F⊥x轴于点F,
∴∠AEO=∠A′FO=90°.
∵点A的坐标为(1,),∴AE=1,OE=,
∴OA=2,∠AOE=30°,由旋转可知∠AOA′=30°,OA′=OA=2,∴∠A′OF=90°-30°-30°=30°,∴A′F=OA′=1,OF=,∴A′(,1).
故选A.
二、填空题
9. 【答案】4 72
10. 【答案】(-2,4)
11. 【答案】(1,0)
12. 【答案】+ [解析] 如图,连接CE′,
∵△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 ,
∴AB=BC=2 ,BD=BE=2.
∵将△BDE绕点B逆时针旋转后得△BD′E′,
∴D′B=BE′=BD=2,∠D′BE′=90°,
∠D′BD=∠ABE′,
∴∠ABD′=∠CBE′,
∴△ABD′≌△CBE′(SAS),
∴∠D′=∠CE′B=45°.
过点B作BH⊥CE′于点H,
在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,
∴CE′=+.故答案为+.
13. 【答案】15°或60° [解析] 分情况讨论:
①若DE⊥BC,设此时直线AD与BC交于点F,则∠BFA=90°-45°=45°,
∴∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;
②若AD⊥BC,则∠BAD=30°,∴α=90°-∠BAD=60°.
故答案为15°或60°.
14. 【答案】y=-x2-2x-3 [解析] 旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
15. 【答案】(4,4)或(1,1)
[解析] (1)若点A和点D、点B和点C分别为对应点,如图①,分别作线段AD,BC的垂直平分线,两条垂直平分线的交点P1(4,4)即为旋转中心;
(2)若点A和点C、点B和点D分别为对应点,如图②,分别作线段AC,BD的垂直平分线,两条垂直平分线的交点P2(1,1)即为旋转中心.综上所述,旋转中心的坐标是(4,4)或(1,1).
16. 【答案】18 [解析] 如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
三、解答题
17. 【答案】
解:(1)旋转角的度数为60°.
(2)证明:由旋转的性质知∠ABC=∠A1BC1=120°,∠C=∠C1,AB=A1B.∵点A,B,C1在同一直线上,∴∠ABC1=180°,∴∠ABA1=∠CBC1=60°,∴∠A1BC=60°,
∵AB=A1B,∴△ABA1是等边三角形,
∴∠AA1B=∠A1BC=60°,
∴AA1∥BC,∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.
18. 【答案】
解:(1)∵将△ABD绕点A逆时针旋转,得到△ACD′,
∴∠DAD′=∠BAC.
∵∠BAC=90°,∴∠DAD′=90°.
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°.
∵∠DAE=45°,
∴∠D′AE=∠DAD′-∠DAE=90°-45°=45°,
∴∠D′AE=∠DAE.
在△AED与△AED′中,
∴△AED≌△AED′(SAS),
∴DE=D′E.
19. 【答案】
解:如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连接DF.由旋转的性质,得CE=CF,AF=BE=2,∠ACF=∠BCE,∠CAF=∠B=45°.
∵∠ACB=90°,∠DCE=45°,
∴∠DCF=∠ACD+∠ACF=∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,∴∠DCE=∠DCF.
在△CDE和△CDF中,
∴△CDE≌△CDF(SAS),∴DE=DF.
∵∠DAF=∠BAC+∠CAF=45°+45°=90°,
∴△ADF是直角三角形,∴DF2=AD2+AF2,∴DE2=AD2+BE2=32+22=13,
∴DE=.
20. 【答案】
解:将△BPC绕点B逆时针旋转60°得到△BP′A(如图).连接PP′,由旋转的性质知△BPP′为等边三角形,AP′=PC=1,
∴PP′=PB=,∠BPP′=∠BP′P=60°.
在△APP′中,∵AP′2+PP′2=12+()2=22=PA2,
∴△APP′是直角三角形,且∠AP′P=90°,
∴∠BP′A=∠BP′P+∠AP′P=60°+90°=150°,
∴∠BPC=∠BP′A=150°.
在Rt△APP′中,∵PA=2,AP′=1,
∴∠APP′=30°.
又∵∠BPP′=60°,
∴∠APB=90°,
∴在Rt△ABP中,AB===,
即等边三角形ABC的边长为.
一、选择题
1. 将下列图形绕其对角线的交点逆时针旋转90°,所得图形一定与原图形重合的是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
2. 如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心是 ( )
A.点A B.点B
C.点C D.点D
3. 如图,将△OAB绕点O逆时针旋转得到△OA′B′,使点B恰好落在边A′B′上.已知AB=4 cm,OB=1 cm,∠B′=60°,那么A′B的长是( )
A.4 cm B.3 cm
C.2 cm D.(4-)cm
4. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A. B.2
C.3 D.2
5. 如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB边的中点是坐标原点O,将正方形绕点C按逆时针方向旋转90°后,点B的对应点B′的坐标是( )
A.(-1,2) B.(1,4)
C.(3,2) D.(-1,0)
6. 如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )
A.(,-1) B.(1,-)
C.(2,0) D.(,0)
7. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为( )
A.4 B.2
C.6 D.2
8. 在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A顺时针旋转30°得到点A′,则点A′的坐标为( )
A.(,1) B.(,-1) C.(2,1) D.(0,2)
二、填空题
9. 如图,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过______次旋转而得到,每一次旋转______度.
10. 在平面直角坐标系中,将点A(4,2)绕原点按逆时针方向旋转90°后,其对应点A′的坐标为________.
11. 如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
12. 如图,△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 .将△BDE绕点B逆时针旋转后得△BD′E′,当点E′恰好落在线段AD′上时,CE′=________.
13. 一副三角尺如图21-K-5放置,将三角尺ADE绕点A逆时针旋转α(0°<α<90°),使得三角尺ADE的一边所在的直线与BC垂直,则α的度数为________.
图21-K-5
14. 把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为_______.
15. 分类讨论如图,点A的坐标为(-1,5),点B的坐标为(3,3),点C的坐标为(5,3),点D的坐标为(3,-1).小明发现线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_________.
教师详解详析
16. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
三、解答题
17. 如图,将一个钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得到△A1BC1,使得点C落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
18. 如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD′.
(1)求∠DAD′的度数;
(2)当∠DAE=45°时,求证:DE=D′E.
19. 如图,在等腰直角三角形ABC中,∠ACB=90°,点D,E在边AB上,且∠DCE=45°,BE=2,AD=3.将△BCE绕点C逆时针旋转90°,画出旋转后的图形,并求DE的长.
20. 如图,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
人教版 九年级数学上册 23.1 图形的旋转 同步训练-答案
一、选择题
1. 【答案】D [解析] 平行四边形绕其对角线的交点旋转能够与原来的图形重合的最小旋转角度数是180°,故A错误;矩形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是180°,故B错误;菱形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是180°,故C错误;正方形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是90°.故选D.
2. 【答案】B [解析] 旋转中心到对应点的距离相等.
3. 【答案】B [解析] ∵旋转前、后的两个图形是全等图形,AB=4 cm,OB=1 cm,∴A′B′=AB=4 cm,OB′=OB=1 cm.
在△OB′B中,∵∠B′=60°,OB′=OB,
∴△OB′B是等边三角形,∴BB′=OB=1 cm,
∴A′B=A′B′-BB′=4-1=3(cm).
4. 【答案】A [解析] ∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5.
∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,
∴AE=4,DE=3,∴BE=1.
在Rt△BED中,BD==.故选A.
5. 【答案】C
6. 【答案】A
7. 【答案】D [解析] 由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2 .
∵DE=2,∴在Rt△ADE中,AE==2 .故选D.
8. 【答案】A [解析] 如图,过点A作AE⊥y轴于点E,过点A′作A′F⊥x轴于点F,
∴∠AEO=∠A′FO=90°.
∵点A的坐标为(1,),∴AE=1,OE=,
∴OA=2,∠AOE=30°,由旋转可知∠AOA′=30°,OA′=OA=2,∴∠A′OF=90°-30°-30°=30°,∴A′F=OA′=1,OF=,∴A′(,1).
故选A.
二、填空题
9. 【答案】4 72
10. 【答案】(-2,4)
11. 【答案】(1,0)
12. 【答案】+ [解析] 如图,连接CE′,
∵△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 ,
∴AB=BC=2 ,BD=BE=2.
∵将△BDE绕点B逆时针旋转后得△BD′E′,
∴D′B=BE′=BD=2,∠D′BE′=90°,
∠D′BD=∠ABE′,
∴∠ABD′=∠CBE′,
∴△ABD′≌△CBE′(SAS),
∴∠D′=∠CE′B=45°.
过点B作BH⊥CE′于点H,
在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,
∴CE′=+.故答案为+.
13. 【答案】15°或60° [解析] 分情况讨论:
①若DE⊥BC,设此时直线AD与BC交于点F,则∠BFA=90°-45°=45°,
∴∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;
②若AD⊥BC,则∠BAD=30°,∴α=90°-∠BAD=60°.
故答案为15°或60°.
14. 【答案】y=-x2-2x-3 [解析] 旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
15. 【答案】(4,4)或(1,1)
[解析] (1)若点A和点D、点B和点C分别为对应点,如图①,分别作线段AD,BC的垂直平分线,两条垂直平分线的交点P1(4,4)即为旋转中心;
(2)若点A和点C、点B和点D分别为对应点,如图②,分别作线段AC,BD的垂直平分线,两条垂直平分线的交点P2(1,1)即为旋转中心.综上所述,旋转中心的坐标是(4,4)或(1,1).
16. 【答案】18 [解析] 如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
三、解答题
17. 【答案】
解:(1)旋转角的度数为60°.
(2)证明:由旋转的性质知∠ABC=∠A1BC1=120°,∠C=∠C1,AB=A1B.∵点A,B,C1在同一直线上,∴∠ABC1=180°,∴∠ABA1=∠CBC1=60°,∴∠A1BC=60°,
∵AB=A1B,∴△ABA1是等边三角形,
∴∠AA1B=∠A1BC=60°,
∴AA1∥BC,∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.
18. 【答案】
解:(1)∵将△ABD绕点A逆时针旋转,得到△ACD′,
∴∠DAD′=∠BAC.
∵∠BAC=90°,∴∠DAD′=90°.
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°.
∵∠DAE=45°,
∴∠D′AE=∠DAD′-∠DAE=90°-45°=45°,
∴∠D′AE=∠DAE.
在△AED与△AED′中,
∴△AED≌△AED′(SAS),
∴DE=D′E.
19. 【答案】
解:如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连接DF.由旋转的性质,得CE=CF,AF=BE=2,∠ACF=∠BCE,∠CAF=∠B=45°.
∵∠ACB=90°,∠DCE=45°,
∴∠DCF=∠ACD+∠ACF=∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,∴∠DCE=∠DCF.
在△CDE和△CDF中,
∴△CDE≌△CDF(SAS),∴DE=DF.
∵∠DAF=∠BAC+∠CAF=45°+45°=90°,
∴△ADF是直角三角形,∴DF2=AD2+AF2,∴DE2=AD2+BE2=32+22=13,
∴DE=.
20. 【答案】
解:将△BPC绕点B逆时针旋转60°得到△BP′A(如图).连接PP′,由旋转的性质知△BPP′为等边三角形,AP′=PC=1,
∴PP′=PB=,∠BPP′=∠BP′P=60°.
在△APP′中,∵AP′2+PP′2=12+()2=22=PA2,
∴△APP′是直角三角形,且∠AP′P=90°,
∴∠BP′A=∠BP′P+∠AP′P=60°+90°=150°,
∴∠BPC=∠BP′A=150°.
在Rt△APP′中,∵PA=2,AP′=1,
∴∠APP′=30°.
又∵∠BPP′=60°,
∴∠APB=90°,
∴在Rt△ABP中,AB===,
即等边三角形ABC的边长为.
同课章节目录
