4.1.1 立体图形与平面图形(第一课时 几何图形的认识)同步练习题(含答案)
文档属性
| 名称 | 4.1.1 立体图形与平面图形(第一课时 几何图形的认识)同步练习题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 几何图形的初步
4.1.1 立体图形与平面图形(第一课时 几何图形的认识)
练习
一、单选题(共10小题)
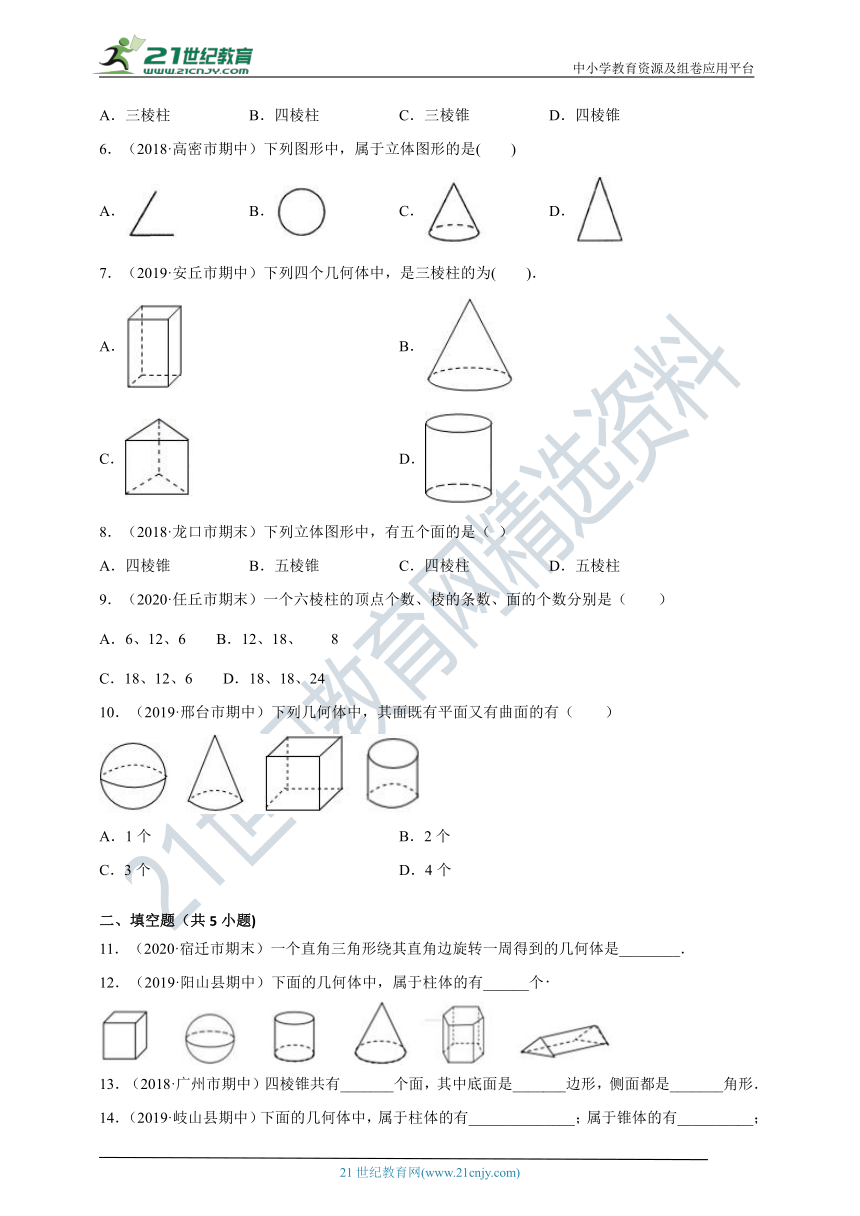
1.(2018·南宁市期末)下面图形中,平面图形是( )
A.B.C.D.
2.(2019·天水市期末)下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥 B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆 D.点、角、线段、长方体
3.(2019·沧州市期中)将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A. B. C. D.
4.(2019·厦门市期末)下列几何体中,是圆柱的为
A. B. C.D.
5.(2019·曲阳县期末)不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是( )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
6.(2018·高密市期中)下列图形中,属于立体图形的是( )
A. B. C. D.
7.(2019·安丘市期中)下列四个几何体中,是三棱柱的为( ).
A. B.
C. D.
8.(2018·龙口市期末)下列立体图形中,有五个面的是( )
A.四棱锥 B.五棱锥 C.四棱柱 D.五棱柱
9.(2020·任丘市期末)一个六棱柱的顶点个数、棱的条数、面的个数分别是( )
A.6、12、6 B.12、18、8
C.18、12、6 D.18、18、24
10.(2019·邢台市期中)下列几何体中,其面既有平面又有曲面的有( )
A.1个 B.2个
C.3个 D.4个
二、填空题(共5小题)
11.(2020·宿迁市期末)一个直角三角形绕其直角边旋转一周得到的几何体是________.
12.(2019·阳山县期中)下面的几何体中,属于柱体的有______个
13.(2018·广州市期中)四棱锥共有_______个面,其中底面是_______边形,侧面都是_______角形.
14.(2019·岐山县期中)下面的几何体中,属于柱体的有______________;属于锥体的有__________;属于球体的有________.
15.(2017·西安市期中)已知三棱柱有个面、个顶点、条棱,四棱柱有个面、个顶点、条棱,五棱柱有个面、个顶点、条棱,,由此可以推测棱柱有__________个面,__________个顶点,__________条棱.
三、解答题(共2小题)
16.(2020叶集区期末)如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.
17.(2019·沈北新区期中)十八世纪瑞士数学家欧拉证明了简单多面体中项点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列儿种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 项点数(V) 面数(F) 棱数(F)
四面体
长方体
正八面体
正十二面体
你发现项点数(V)、面数(F)、棱数(F)之间存在的关系式是__________________________.
(2)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是 20;
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
答案
一、单选题(共10小题)
1.D.2.C.3.D4.A.5.D6.C.7.C8.A.9.B.10.B
二、填空题(共5小题)
11.【答案】圆锥【解析】
解:一个直角三角形绕其直角边旋转一周得到的几何体是圆锥.故答案为圆锥.
12.答案】4【详解】柱体分为圆柱和棱柱,所以柱体有:第1、3、5、6,
故答案为4个.
13【答案】五 四 三 【详解】
四棱锥共有五个面,其中底面是四边形,侧面都是三角形.
故答案为:(1)五;(2)四边;(3)三角.
14.【答案】①③⑤⑥ ④ ② 【解析】
试题解析:柱体分为圆柱和棱柱,所以柱体有:①③⑤⑥;
锥体包括圆锥和棱锥,所以锥体有④,
球体②.
故答案为①③⑤⑥;④; ②
15.【答案】n+2 2n 3n 【详解】
n棱柱有(n+2)个面,2n个顶点和3n条棱
故答案为:n+2、2n、3n
三、解答题(共2小题)
16.【答案】(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.【解析】
试题分析:结合已知三棱柱、四棱柱、五棱柱和六棱柱的特点,可知棱柱一定有个面,条棱和个顶点.
试题解析:(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为(1)6,12,8;(2)8,18,12;(3)
17.【答案】(1) 见解析,V+F-E=2;(2) 20;(3)26
【分析】
(1)观察表格可以看出:顶点数+面数-棱数=2,关系式为:V+F-E=2;
(2)代入(1)中公式进行计算;
(3)根据欧拉公式可得顶点数+面数-棱数=2,然后表示出棱数,进而可得面数.
【详解】
解:(1)根据题意得如下图
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
长方体 8 6 12
正八面体 6 8 12
正十二面体 20 12 30
∵4+4-6=2,8+6-12=2,6+8-12=2,
∴顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)由(1)可知:V+F-E=2,
∵一个多面体的面数比顶点数小8,且有30条棱,
∴V+V-8-30=2,即V=20;
(3)∵有48个顶点,每个顶点处都有3条棱,两点确定一条直线;
∴共有48×3÷2=72条棱,
设总面数为F,
48+F-72=2,
解得F=26,
∴x+y=26.
_21?????????è?????(www.21cnjy.com)_
第四章 几何图形的初步
4.1.1 立体图形与平面图形(第一课时 几何图形的认识)
练习
一、单选题(共10小题)
1.(2018·南宁市期末)下面图形中,平面图形是( )
A.B.C.D.
2.(2019·天水市期末)下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥 B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆 D.点、角、线段、长方体
3.(2019·沧州市期中)将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A. B. C. D.
4.(2019·厦门市期末)下列几何体中,是圆柱的为
A. B. C.D.
5.(2019·曲阳县期末)不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是( )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
6.(2018·高密市期中)下列图形中,属于立体图形的是( )
A. B. C. D.
7.(2019·安丘市期中)下列四个几何体中,是三棱柱的为( ).
A. B.
C. D.
8.(2018·龙口市期末)下列立体图形中,有五个面的是( )
A.四棱锥 B.五棱锥 C.四棱柱 D.五棱柱
9.(2020·任丘市期末)一个六棱柱的顶点个数、棱的条数、面的个数分别是( )
A.6、12、6 B.12、18、8
C.18、12、6 D.18、18、24
10.(2019·邢台市期中)下列几何体中,其面既有平面又有曲面的有( )
A.1个 B.2个
C.3个 D.4个
二、填空题(共5小题)
11.(2020·宿迁市期末)一个直角三角形绕其直角边旋转一周得到的几何体是________.
12.(2019·阳山县期中)下面的几何体中,属于柱体的有______个
13.(2018·广州市期中)四棱锥共有_______个面,其中底面是_______边形,侧面都是_______角形.
14.(2019·岐山县期中)下面的几何体中,属于柱体的有______________;属于锥体的有__________;属于球体的有________.
15.(2017·西安市期中)已知三棱柱有个面、个顶点、条棱,四棱柱有个面、个顶点、条棱,五棱柱有个面、个顶点、条棱,,由此可以推测棱柱有__________个面,__________个顶点,__________条棱.
三、解答题(共2小题)
16.(2020叶集区期末)如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.
17.(2019·沈北新区期中)十八世纪瑞士数学家欧拉证明了简单多面体中项点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列儿种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 项点数(V) 面数(F) 棱数(F)
四面体
长方体
正八面体
正十二面体
你发现项点数(V)、面数(F)、棱数(F)之间存在的关系式是__________________________.
(2)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是 20;
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
答案
一、单选题(共10小题)
1.D.2.C.3.D4.A.5.D6.C.7.C8.A.9.B.10.B
二、填空题(共5小题)
11.【答案】圆锥【解析】
解:一个直角三角形绕其直角边旋转一周得到的几何体是圆锥.故答案为圆锥.
12.答案】4【详解】柱体分为圆柱和棱柱,所以柱体有:第1、3、5、6,
故答案为4个.
13【答案】五 四 三 【详解】
四棱锥共有五个面,其中底面是四边形,侧面都是三角形.
故答案为:(1)五;(2)四边;(3)三角.
14.【答案】①③⑤⑥ ④ ② 【解析】
试题解析:柱体分为圆柱和棱柱,所以柱体有:①③⑤⑥;
锥体包括圆锥和棱锥,所以锥体有④,
球体②.
故答案为①③⑤⑥;④; ②
15.【答案】n+2 2n 3n 【详解】
n棱柱有(n+2)个面,2n个顶点和3n条棱
故答案为:n+2、2n、3n
三、解答题(共2小题)
16.【答案】(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.【解析】
试题分析:结合已知三棱柱、四棱柱、五棱柱和六棱柱的特点,可知棱柱一定有个面,条棱和个顶点.
试题解析:(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为(1)6,12,8;(2)8,18,12;(3)
17.【答案】(1) 见解析,V+F-E=2;(2) 20;(3)26
【分析】
(1)观察表格可以看出:顶点数+面数-棱数=2,关系式为:V+F-E=2;
(2)代入(1)中公式进行计算;
(3)根据欧拉公式可得顶点数+面数-棱数=2,然后表示出棱数,进而可得面数.
【详解】
解:(1)根据题意得如下图
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
长方体 8 6 12
正八面体 6 8 12
正十二面体 20 12 30
∵4+4-6=2,8+6-12=2,6+8-12=2,
∴顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)由(1)可知:V+F-E=2,
∵一个多面体的面数比顶点数小8,且有30条棱,
∴V+V-8-30=2,即V=20;
(3)∵有48个顶点,每个顶点处都有3条棱,两点确定一条直线;
∴共有48×3÷2=72条棱,
设总面数为F,
48+F-72=2,
解得F=26,
∴x+y=26.
_21?????????è?????(www.21cnjy.com)_
