3.2.1几类不同增长的函数模型
图片预览







文档简介
(共24张PPT)
3.2 函数模型及其应用
有人说,一张普通的报纸对折30次后,厚度会超过10座珠穆朗玛峰的高度,会是真的吗?
“陛下,请您在这张棋盘的第一个小格内,赏给我两粒麦子,在第二个小格内给四粒,第三格内给八粒,用这样下去,每一小格内都比前一小格加一倍。陛下,把这样摆满棋盘上所有64格的麦粒,都赏给您的仆人吧! ”
“爱卿,你所求的并不多啊!”
[ 例1] 假设你有一笔资金用于投资,现有三种投资方案
供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
①例1涉及哪些数量关系?
②如何用函数描述这些数量关系?
用3分钟时间阅读课本95页例1,边阅读边思考下面的问题:
投资天数、回报金额
③三个函数模型的增减性如何?
④要对三个方案作出选择,就要对它们的增长情况进行分析,如何分析?
每天的回报数、增加量、累计回报数
我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据。
解:设第x天所得回报为y元,则
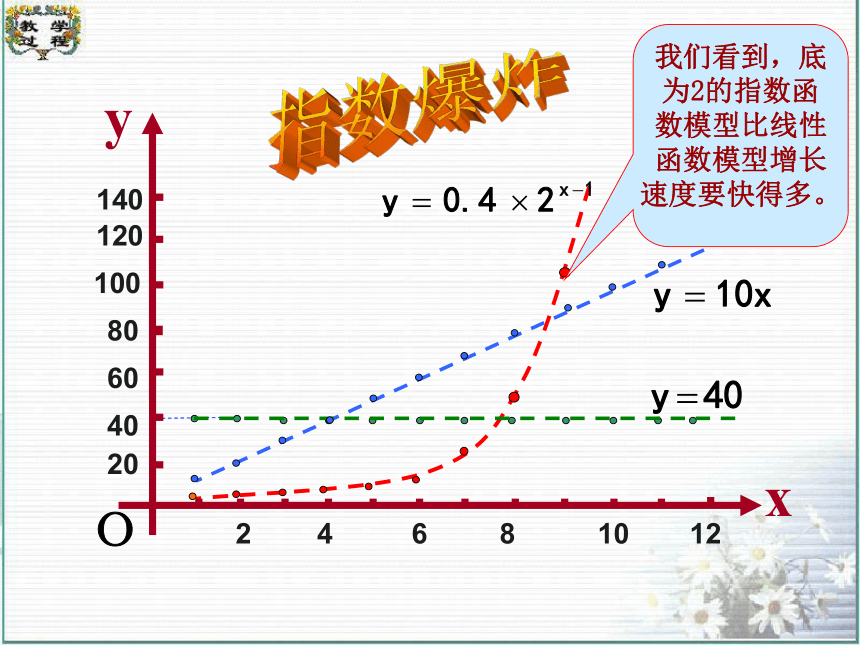
方案一:每天回报40元; y=40 (x∈N*)
方案二:第一天回报10元,以后每天比前一
天多回报10元; y=10x (x∈N*)
方案三:第一天回报0.4元,以后每天的回报
比前一天翻一番。y=0.4×2x-1 (x∈N*)
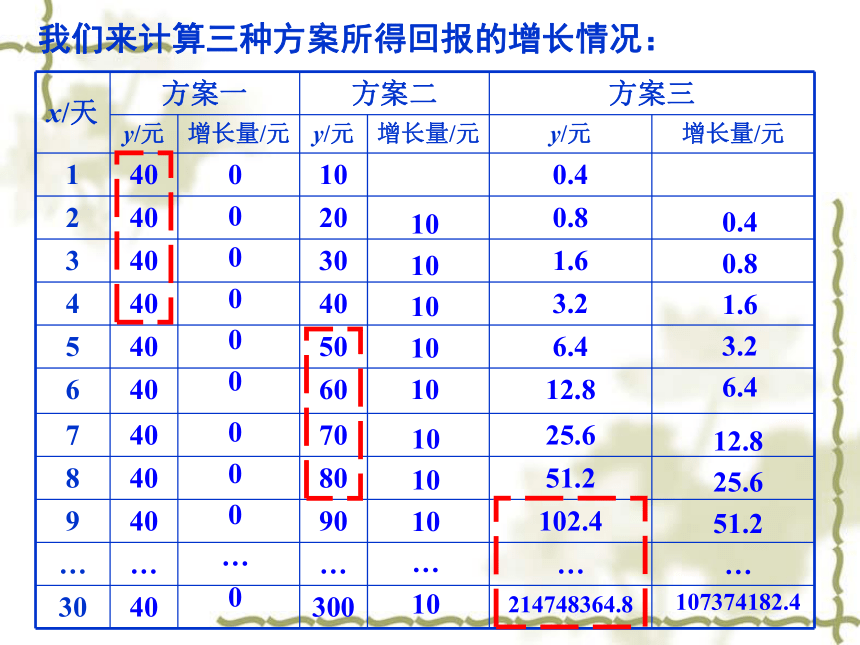
x/天 方案一 方案二 方案三
y/元 增长量/元 y/元 增长量/元 y/元 增长量/元
1 40 10 0.4
2 40 20 0.8
3 40 30 1.6
4 40 40 3.2
5 40 50 6.4
6 40 60 12.8
7 40 70 25.6
8 40 80 51.2
9 40 90 102.4
… … … …
30 40 300 214748364.8
0
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
…
107374182.4
我们来计算三种方案所得回报的增长情况:
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。
1 2 3 4 5 6 7 8 9 10 11 … 30
方案一 40 80 120 160 200 240 280 320 360 400 440 … 1200
方案二 10 30 60 100 150 210 280 360 450 550 660 … 4650
方案三 0 1 2.8 6 12 25 50.8 102 204 409 819 … 429496729.2
例1累计回报表
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
例1体会:
确定函数模型
利用数据表格、函数图象讨论模型
体会直线上升、指数爆炸等不同函数类、模型增长的含义
第二节
一次函数
对数函数
指数函数
①例2涉及了哪几类函数模型?
用3分钟时间认真阅读例2,边阅读边思考下面的问题:
②公司有哪些要求呢?
[例2] 某公司为了实现1000万元利润的目标,准备制定
一个激励销售人员的奖励方案:在销售利润达到10万
元时,按销售利润进行奖励,且奖金y (单位:万元)
随销售利润x(单位:万元)的增加而增加,但奖金
总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求?
3、销售利润达到10万元时进行奖励;
1、奖金总数不超过5万元;
2、奖金不超过利润的25%;
4、公司总的利润目标为1000万元。
因此我们需要在区间[10,1000]上考虑哪种模型符合要求对吧?
尝试作函数:
y=0.25x, y=log7x+1,
y=1.002x,及y=5的图象.并思考:
不妨试一试!
1.如何利用它们的图象作出选择呢?
2.这三种增长有什么不同呢?
▲ 通过观察图象,你认为哪个模型符合公司的奖励方案?
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
①对于模型y=0.25x,它在区间[10,1000]上递增,
当x>20时,y>5,因此该模型不符合要求;
②对于模型y=1.002x,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x>806时,y>5,因此
该模型不符合要求;
③对于模型y=log7x+1,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x=1000时,
y=log71000+1≈4.55<5,所以它符合奖金总数不超过
5万元的要求;
是否满足
“奖金不超过利润的25%”呢?
★按模型y=log7x+1奖励时,奖金是否不超过利润的25%呢?
解:当x∈[10,1000]时,要使y≤0.25x成立,
令f(x)= log7x+1-0.25x,当x∈[10,1000]时,
是否有f(x) ≤0恒成立
即当x∈[10,1000]时,f(x)= log7x+1-0.25x的
图象是否在x轴下方
作f(x)= log7x+1-0.25x的图象如下:
只需log7x+1≤0.25x成立,
即log7x+1-0.25x ≤0。
y
x
1
2
3
4
5
6
7
8
0
f(x)=log7x+1-0.25x
1
-1
根据图象观察,f(x)=log7x+1-0.25x的图象在区间[10,1000]内的确在x轴的下方.
f(x)=log7x+1-0.25x
这说明,按模型y=log7x+1奖励,奖金不会超过利润的25%.
所以,模型 确实能符合公司的要求。
确定函数模型
利用数据表格、函数图象讨论模型
体会直线上升、指数爆炸、对数增长等不同函数模型增长的含义
实际应用问题
审 题
(设)
分析、联想、抽象、转化
构建数学模型
数学化
(列)
寻找解题思路
(解)
解答数学问题
还原
(答)
课外活动:收集一些社会生活中普遍使用的递增的一次函数、指数函数、对数函数的实例,对它们的增长速度进行比较,了解函数模型的广泛应用。
作 业
教材P107 习题3.2 1-4
3.2 函数模型及其应用
有人说,一张普通的报纸对折30次后,厚度会超过10座珠穆朗玛峰的高度,会是真的吗?
“陛下,请您在这张棋盘的第一个小格内,赏给我两粒麦子,在第二个小格内给四粒,第三格内给八粒,用这样下去,每一小格内都比前一小格加一倍。陛下,把这样摆满棋盘上所有64格的麦粒,都赏给您的仆人吧! ”
“爱卿,你所求的并不多啊!”
[ 例1] 假设你有一笔资金用于投资,现有三种投资方案
供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
①例1涉及哪些数量关系?
②如何用函数描述这些数量关系?
用3分钟时间阅读课本95页例1,边阅读边思考下面的问题:
投资天数、回报金额
③三个函数模型的增减性如何?
④要对三个方案作出选择,就要对它们的增长情况进行分析,如何分析?
每天的回报数、增加量、累计回报数
我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据。
解:设第x天所得回报为y元,则
方案一:每天回报40元; y=40 (x∈N*)
方案二:第一天回报10元,以后每天比前一
天多回报10元; y=10x (x∈N*)
方案三:第一天回报0.4元,以后每天的回报
比前一天翻一番。y=0.4×2x-1 (x∈N*)
x/天 方案一 方案二 方案三
y/元 增长量/元 y/元 增长量/元 y/元 增长量/元
1 40 10 0.4
2 40 20 0.8
3 40 30 1.6
4 40 40 3.2
5 40 50 6.4
6 40 60 12.8
7 40 70 25.6
8 40 80 51.2
9 40 90 102.4
… … … …
30 40 300 214748364.8
0
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
…
107374182.4
我们来计算三种方案所得回报的增长情况:
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。
1 2 3 4 5 6 7 8 9 10 11 … 30
方案一 40 80 120 160 200 240 280 320 360 400 440 … 1200
方案二 10 30 60 100 150 210 280 360 450 550 660 … 4650
方案三 0 1 2.8 6 12 25 50.8 102 204 409 819 … 429496729.2
例1累计回报表
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
例1体会:
确定函数模型
利用数据表格、函数图象讨论模型
体会直线上升、指数爆炸等不同函数类、模型增长的含义
第二节
一次函数
对数函数
指数函数
①例2涉及了哪几类函数模型?
用3分钟时间认真阅读例2,边阅读边思考下面的问题:
②公司有哪些要求呢?
[例2] 某公司为了实现1000万元利润的目标,准备制定
一个激励销售人员的奖励方案:在销售利润达到10万
元时,按销售利润进行奖励,且奖金y (单位:万元)
随销售利润x(单位:万元)的增加而增加,但奖金
总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求?
3、销售利润达到10万元时进行奖励;
1、奖金总数不超过5万元;
2、奖金不超过利润的25%;
4、公司总的利润目标为1000万元。
因此我们需要在区间[10,1000]上考虑哪种模型符合要求对吧?
尝试作函数:
y=0.25x, y=log7x+1,
y=1.002x,及y=5的图象.并思考:
不妨试一试!
1.如何利用它们的图象作出选择呢?
2.这三种增长有什么不同呢?
▲ 通过观察图象,你认为哪个模型符合公司的奖励方案?
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
①对于模型y=0.25x,它在区间[10,1000]上递增,
当x>20时,y>5,因此该模型不符合要求;
②对于模型y=1.002x,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x>806时,y>5,因此
该模型不符合要求;
③对于模型y=log7x+1,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x=1000时,
y=log71000+1≈4.55<5,所以它符合奖金总数不超过
5万元的要求;
是否满足
“奖金不超过利润的25%”呢?
★按模型y=log7x+1奖励时,奖金是否不超过利润的25%呢?
解:当x∈[10,1000]时,要使y≤0.25x成立,
令f(x)= log7x+1-0.25x,当x∈[10,1000]时,
是否有f(x) ≤0恒成立
即当x∈[10,1000]时,f(x)= log7x+1-0.25x的
图象是否在x轴下方
作f(x)= log7x+1-0.25x的图象如下:
只需log7x+1≤0.25x成立,
即log7x+1-0.25x ≤0。
y
x
1
2
3
4
5
6
7
8
0
f(x)=log7x+1-0.25x
1
-1
根据图象观察,f(x)=log7x+1-0.25x的图象在区间[10,1000]内的确在x轴的下方.
f(x)=log7x+1-0.25x
这说明,按模型y=log7x+1奖励,奖金不会超过利润的25%.
所以,模型 确实能符合公司的要求。
确定函数模型
利用数据表格、函数图象讨论模型
体会直线上升、指数爆炸、对数增长等不同函数模型增长的含义
实际应用问题
审 题
(设)
分析、联想、抽象、转化
构建数学模型
数学化
(列)
寻找解题思路
(解)
解答数学问题
还原
(答)
课外活动:收集一些社会生活中普遍使用的递增的一次函数、指数函数、对数函数的实例,对它们的增长速度进行比较,了解函数模型的广泛应用。
作 业
教材P107 习题3.2 1-4
