3.1.1倾斜角与斜率
图片预览

文档简介
(共13张PPT)
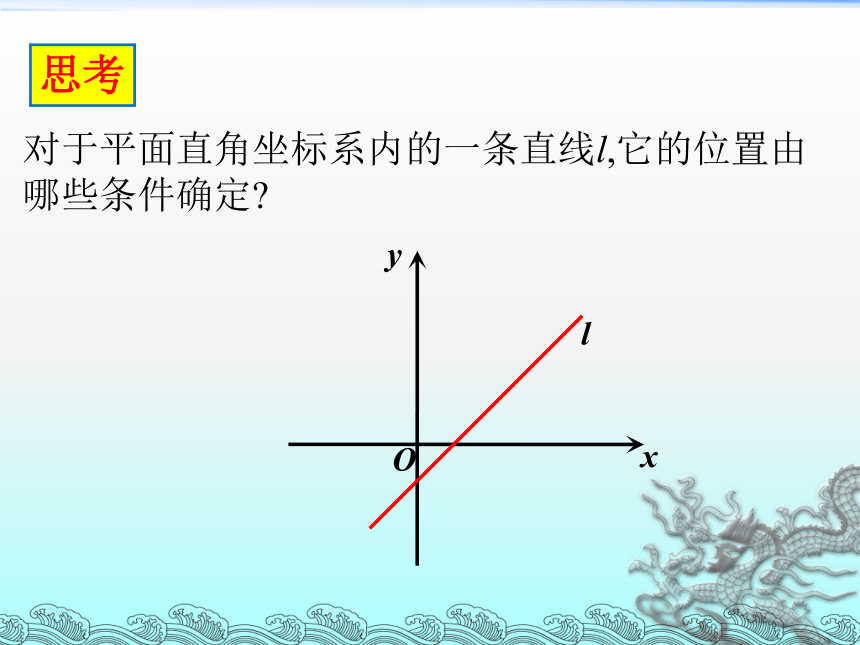
对于平面直角坐标系内的一条直线l,它的位置由哪些条件确定
x
y
O
l
思考
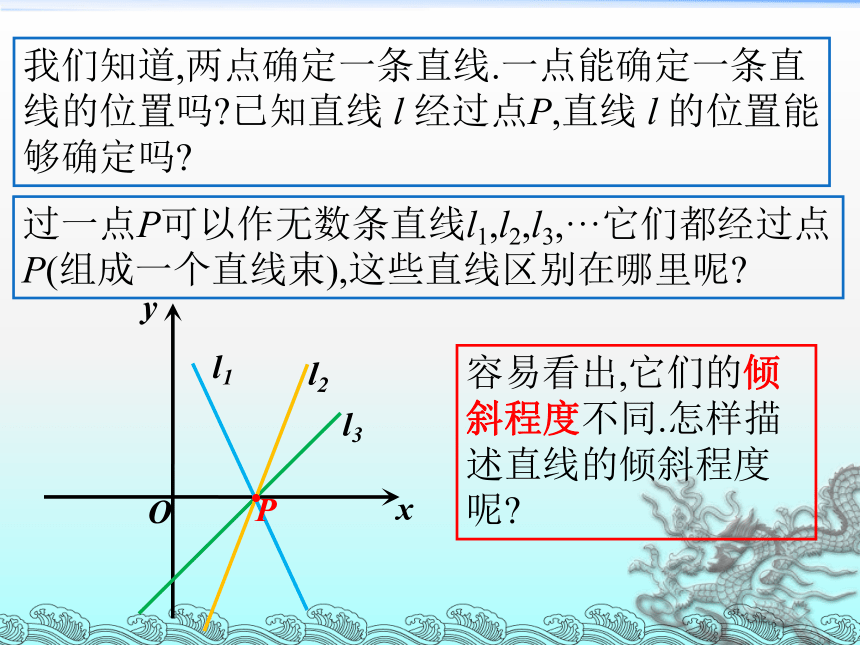
我们知道,两点确定一条直线.一点能确定一条直线的位置吗 已知直线 l 经过点P,直线 l 的位置能够确定吗
x
y
O
l3
l2
l1
P
过一点P可以作无数条直线l1,l2,l3,···它们都经过点P(组成一个直线束),这些直线区别在哪里呢
容易看出,它们的倾斜程度不同.怎样描述直线的倾斜程度呢
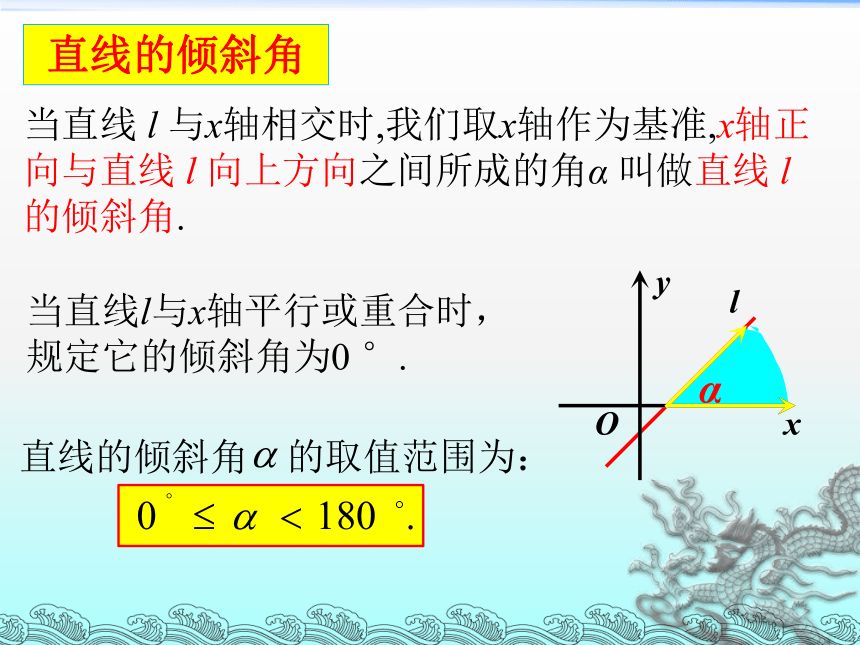
当直线 l 与x轴相交时,我们取x轴作为基准,x轴正向与直线 l 向上方向之间所成的角α 叫做直线 l 的倾斜角.
x
y
O
l
当直线l与x轴平行或重合时,规定它的倾斜角为0 °.
直线的倾斜角 的取值范围为:
直线的倾斜角
α
x
y
O
l
x
y
O
l3
l2
l1
P
x
y
O
l
P
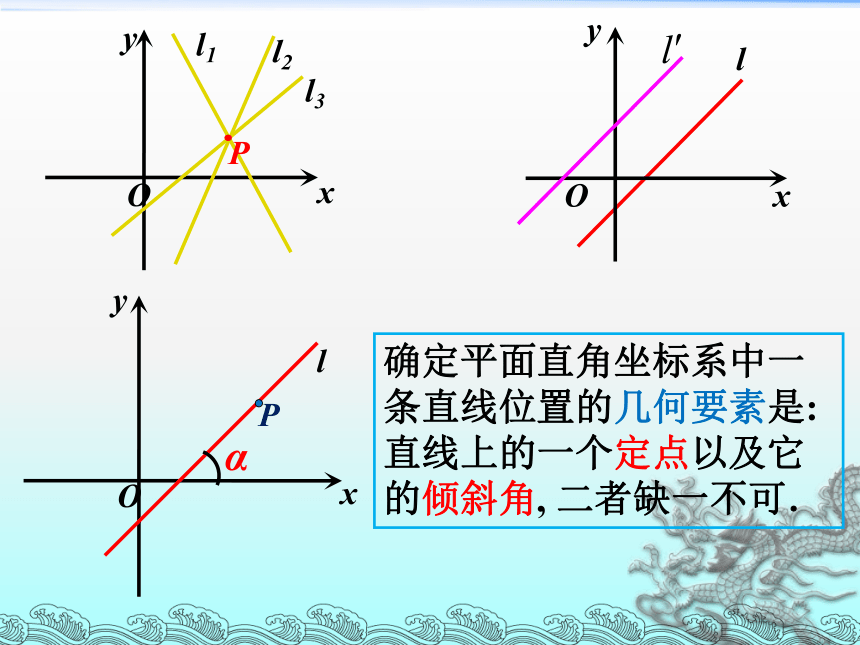
确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角, 二者缺一不可.
α
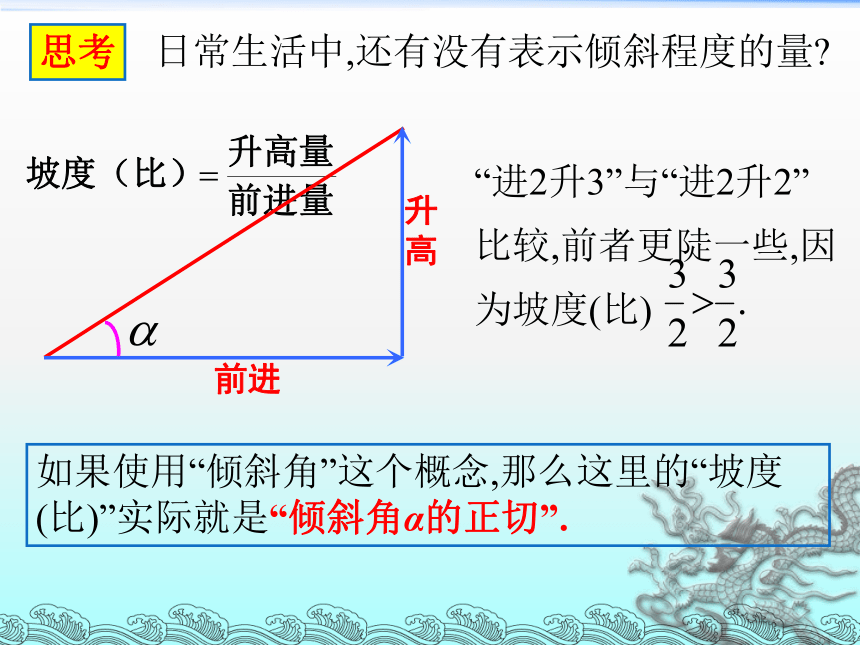
日常生活中,还有没有表示倾斜程度的量
思考
前进
升
高
“进2升3”与“进2升2”比较,前者更陡一些,因为坡度(比)
如果使用“倾斜角”这个概念,那么这里的“坡度(比)”实际就是“倾斜角α的正切”.
一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即
直线的斜率
如:倾斜角α=45°时,直线的斜率k=tan45° =1;
倾斜角α=135°时,直线的斜率k=tan135° =-1.
倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为0°时,k=0.
当α为锐角时,
在直角 中
设直线P1 P2的倾斜角为α(α ≠90°),当直线P1 P2的方向(即从P1指向P2的方向)向上时,过点P1作 x 轴的平行线,过点P2作 y 轴的平行线,两线相交于点 Q,于是点Q的坐标为(x2,y1 ).
探究 已知直线上两点的坐标,如何计算直线的斜率
给定两点P1(x1, y1),P2(x2, y2), 并且x1 ≠x2,如何计算直线P1P2的斜率k.
当α为钝角时,
在直角 中
当P2P1的方向向上时,也有
(1)已知直线上两点 A(a1, a2),B(b1, b2) ,运用上述公式计算直线AB斜率时,与A,B两点坐标的顺序有关吗
无关
(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
不适用
经过两点P1(x1, y1),P2(x2, y2) (x1 ≠x2)的直线的斜率公式
思考
(3)当直线平行于x轴,或与x轴重合时,上述式子还适用吗?为什么?
适用
例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线l1,l2,l3及l4.
即
解:设A 1(x1, y1),是直线l1上的一点,根据斜率公式有
设x1=1,则y1 =1,于是 A1的坐标是(1,1).过原点及A1(1,1) 的直线即为l1 .
分析:要画出过原点l1的直线,只须再找出位于l1上的某一点A1来, A1的坐标可以有的斜率确定.
对于平面直角坐标系内的一条直线l,它的位置由哪些条件确定
x
y
O
l
思考
我们知道,两点确定一条直线.一点能确定一条直线的位置吗 已知直线 l 经过点P,直线 l 的位置能够确定吗
x
y
O
l3
l2
l1
P
过一点P可以作无数条直线l1,l2,l3,···它们都经过点P(组成一个直线束),这些直线区别在哪里呢
容易看出,它们的倾斜程度不同.怎样描述直线的倾斜程度呢
当直线 l 与x轴相交时,我们取x轴作为基准,x轴正向与直线 l 向上方向之间所成的角α 叫做直线 l 的倾斜角.
x
y
O
l
当直线l与x轴平行或重合时,规定它的倾斜角为0 °.
直线的倾斜角 的取值范围为:
直线的倾斜角
α
x
y
O
l
x
y
O
l3
l2
l1
P
x
y
O
l
P
确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角, 二者缺一不可.
α
日常生活中,还有没有表示倾斜程度的量
思考
前进
升
高
“进2升3”与“进2升2”比较,前者更陡一些,因为坡度(比)
如果使用“倾斜角”这个概念,那么这里的“坡度(比)”实际就是“倾斜角α的正切”.
一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即
直线的斜率
如:倾斜角α=45°时,直线的斜率k=tan45° =1;
倾斜角α=135°时,直线的斜率k=tan135° =-1.
倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为0°时,k=0.
当α为锐角时,
在直角 中
设直线P1 P2的倾斜角为α(α ≠90°),当直线P1 P2的方向(即从P1指向P2的方向)向上时,过点P1作 x 轴的平行线,过点P2作 y 轴的平行线,两线相交于点 Q,于是点Q的坐标为(x2,y1 ).
探究 已知直线上两点的坐标,如何计算直线的斜率
给定两点P1(x1, y1),P2(x2, y2), 并且x1 ≠x2,如何计算直线P1P2的斜率k.
当α为钝角时,
在直角 中
当P2P1的方向向上时,也有
(1)已知直线上两点 A(a1, a2),B(b1, b2) ,运用上述公式计算直线AB斜率时,与A,B两点坐标的顺序有关吗
无关
(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
不适用
经过两点P1(x1, y1),P2(x2, y2) (x1 ≠x2)的直线的斜率公式
思考
(3)当直线平行于x轴,或与x轴重合时,上述式子还适用吗?为什么?
适用
例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线l1,l2,l3及l4.
即
解:设A 1(x1, y1),是直线l1上的一点,根据斜率公式有
设x1=1,则y1 =1,于是 A1的坐标是(1,1).过原点及A1(1,1) 的直线即为l1 .
分析:要画出过原点l1的直线,只须再找出位于l1上的某一点A1来, A1的坐标可以有的斜率确定.
