高中数学人教A版(2019)必修第一册4.2指数函数的图象与性质第一课时课件
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册4.2指数函数的图象与性质第一课时课件 |  | |
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 07:32:09 | ||
图片预览





文档简介
(共21张PPT)
4.2
指数函数的图象和性质
第一课时
人教A版《数学》必修第一册
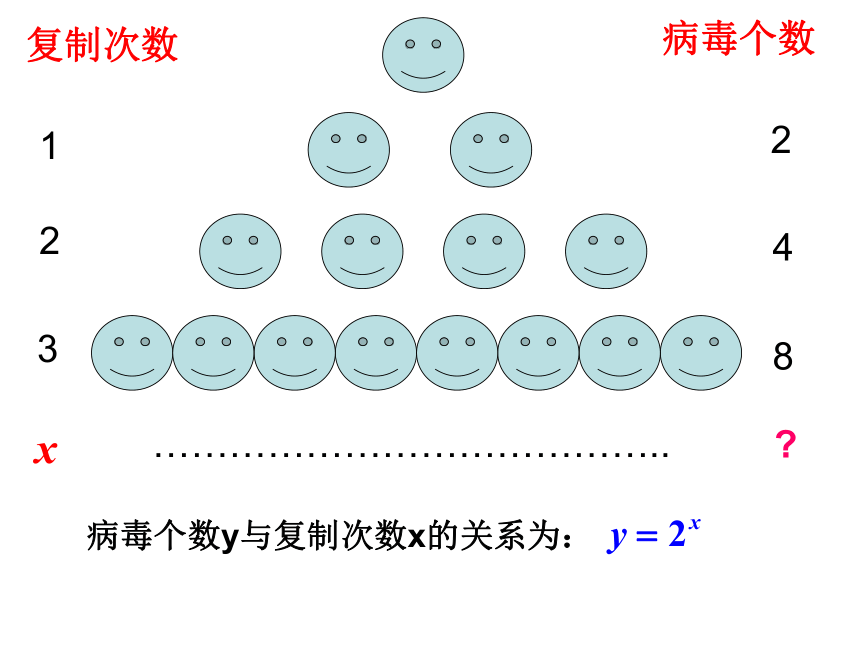
我是新冠病毒,在传播
时我可以由一个复制成二个,
二个复制成四个,……,我
复制x次后,得到的病毒个数
y与x有怎样的关系?
问题一
复制次数
病毒个数
1
2
3
2
4
8
…………………………………..
?
病毒个数y与复制次数x的关系为:
?
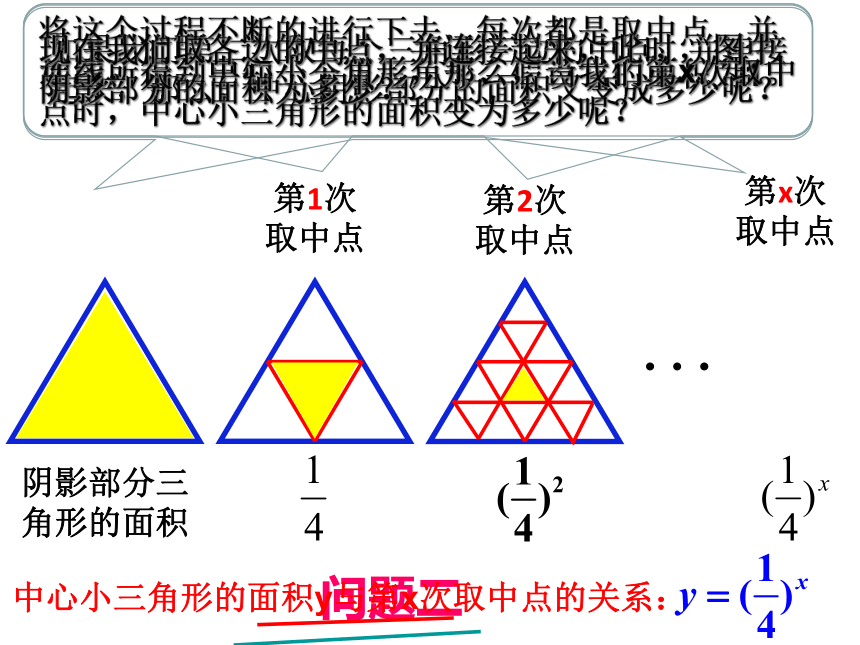
第1次
取中点
第2次
取中点
第x次
取中点
阴影部分三角形的面积
如图所示,已知一个正三角形,假设它的面积为1。
如果我们第二次取每个三角形三边的中点,并连接起来,那么,中心阴影部分的面积又变成多少呢?
将这个过程不断的进行下去,每次都是取中点,并连线,得到中心小三角形,那么,当我们第x次取中点时,中心小三角形的面积变为多少呢?
现在我们取各边的中点,并连接起来,此时,图中阴影部分的面积为多少?
问题二
中心小三角形的面积y与第x次取中点的关系:
探究
问题一中函数
与问题二中函
数
的解析式有什么共同特征?
(1)
指数为自变量;
(2)
底数为常数;
(3)
幂的系数为1.
指数函数的定义
函数
叫做指数函数,
?
函数的定义域是
.
其中
是自变量,
下列函数中,哪些是指数函数?
我是
我也不是
你答对了吗?
概念辨析
小菜一碟
我也是
0
1
1
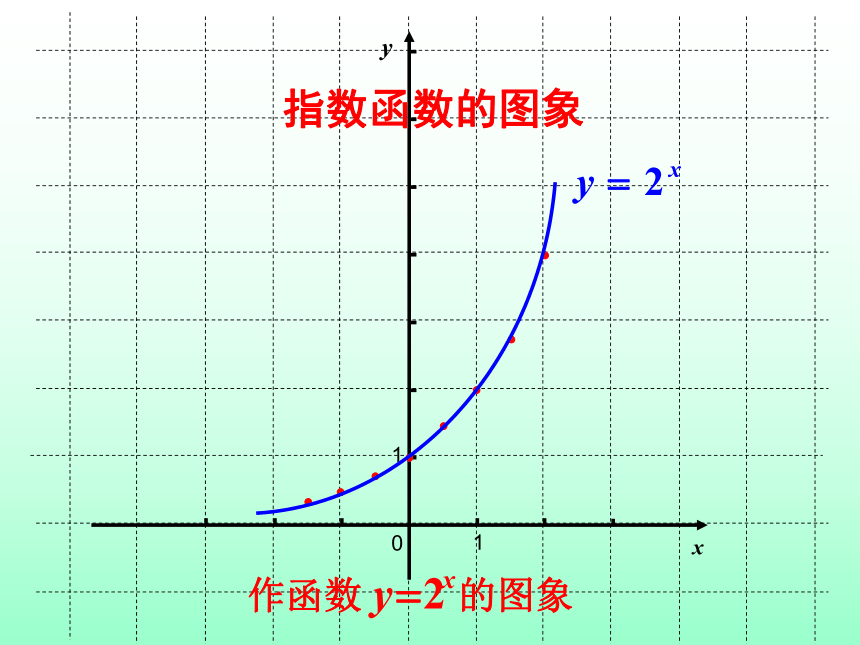
作函数
的图象
指数函数的图象
0
1
1
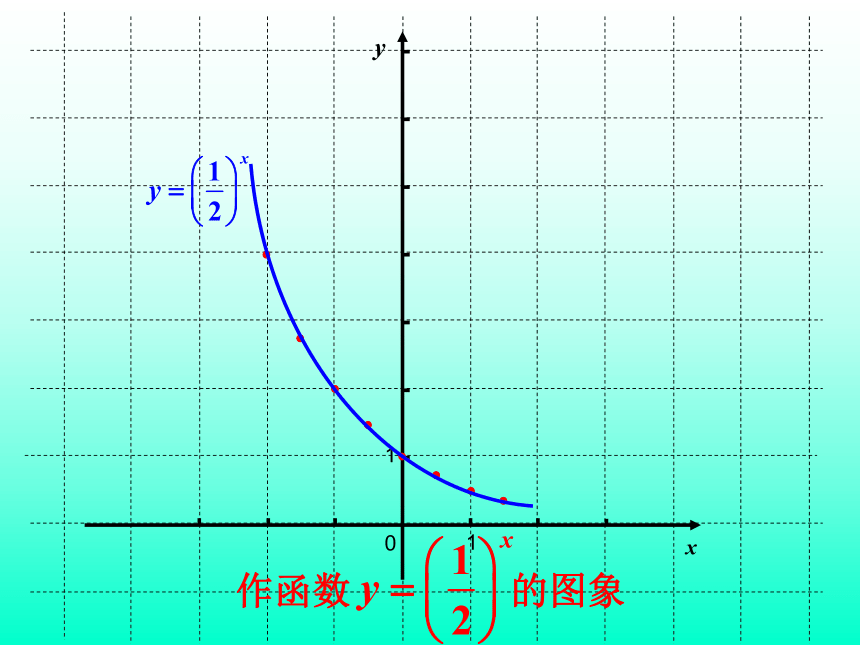
作函数
的图象
1
1
1
1
1
1
1
1
指数函数的图象和性质
性
质
定义域:
定义域:
值域:
值域:
恒过定点:
恒过定点:
R
R
(0,1)
(0,1)
(0,+∞)
(0,+∞)
(0,1)
(0,1)
图
象
(0,1)
(0,1)
指数函数的图象及性质
性
质
当
时,
_____
当
时,
当
时,
当
时,
_____
在R上是单调______
在R上是单调_______
增函数
减函数
图
象
(0,1)
(0,1)
指数函数的图象及性质
例1、比较下列各组数的大小.
>
<
<
>
歪歪
同底用单调性
不同底化为同底
不能化为同底
找中间量
3.数学思想方法:
特殊到一般,分类讨论,数形结合.
作业
你有什么收获
4.
数学源于生活,服务生活,
生活中的数学无处不在.
1.
指数函数定义:
2.
指数函数的图象性质.
作业布置
课后思考:
课后作业:
课本P118
1、2、3、4、5、6
1、比较大小:
2、指数函数
与
的图象关于y轴对称,为什么?
3、设
都是不等于1的正数,
在同
一坐标系中的图象如图所示,则
的大小
关系是______.
同学们再见!
0
1
1
指数函数图象与底数的关系
底数互为倒数的两个指数函数图象关于y轴对称.
0
1
1
0
1
1
指数函数图象与底数的关系
第一象限沿箭头方向,底数增大.
li1
zybz
例2、据国际原子能机构的调查数据显示,2011年在日本福岛核电站某受污染地区的辐射强度约为安全标准的1000倍。专家估计随着放射性物质的衰变和环境的稀释,每过一年,辐射强度会下降一半。问从2011年开始,至少经过多少年,该地区的辐射强度才能达到安全标准?
解:设至少经过
年,该地区的辐射强度才能达到安全标准.
答:至少经过10年,该地区的辐射强度才能达到安全标准.
在R上单调递减,
4.2
指数函数的图象和性质
第一课时
人教A版《数学》必修第一册
我是新冠病毒,在传播
时我可以由一个复制成二个,
二个复制成四个,……,我
复制x次后,得到的病毒个数
y与x有怎样的关系?
问题一
复制次数
病毒个数
1
2
3
2
4
8
…………………………………..
?
病毒个数y与复制次数x的关系为:
?
第1次
取中点
第2次
取中点
第x次
取中点
阴影部分三角形的面积
如图所示,已知一个正三角形,假设它的面积为1。
如果我们第二次取每个三角形三边的中点,并连接起来,那么,中心阴影部分的面积又变成多少呢?
将这个过程不断的进行下去,每次都是取中点,并连线,得到中心小三角形,那么,当我们第x次取中点时,中心小三角形的面积变为多少呢?
现在我们取各边的中点,并连接起来,此时,图中阴影部分的面积为多少?
问题二
中心小三角形的面积y与第x次取中点的关系:
探究
问题一中函数
与问题二中函
数
的解析式有什么共同特征?
(1)
指数为自变量;
(2)
底数为常数;
(3)
幂的系数为1.
指数函数的定义
函数
叫做指数函数,
?
函数的定义域是
.
其中
是自变量,
下列函数中,哪些是指数函数?
我是
我也不是
你答对了吗?
概念辨析
小菜一碟
我也是
0
1
1
作函数
的图象
指数函数的图象
0
1
1
作函数
的图象
1
1
1
1
1
1
1
1
指数函数的图象和性质
性
质
定义域:
定义域:
值域:
值域:
恒过定点:
恒过定点:
R
R
(0,1)
(0,1)
(0,+∞)
(0,+∞)
(0,1)
(0,1)
图
象
(0,1)
(0,1)
指数函数的图象及性质
性
质
当
时,
_____
当
时,
当
时,
当
时,
_____
在R上是单调______
在R上是单调_______
增函数
减函数
图
象
(0,1)
(0,1)
指数函数的图象及性质
例1、比较下列各组数的大小.
>
<
<
>
歪歪
同底用单调性
不同底化为同底
不能化为同底
找中间量
3.数学思想方法:
特殊到一般,分类讨论,数形结合.
作业
你有什么收获
4.
数学源于生活,服务生活,
生活中的数学无处不在.
1.
指数函数定义:
2.
指数函数的图象性质.
作业布置
课后思考:
课后作业:
课本P118
1、2、3、4、5、6
1、比较大小:
2、指数函数
与
的图象关于y轴对称,为什么?
3、设
都是不等于1的正数,
在同
一坐标系中的图象如图所示,则
的大小
关系是______.
同学们再见!
0
1
1
指数函数图象与底数的关系
底数互为倒数的两个指数函数图象关于y轴对称.
0
1
1
0
1
1
指数函数图象与底数的关系
第一象限沿箭头方向,底数增大.
li1
zybz
例2、据国际原子能机构的调查数据显示,2011年在日本福岛核电站某受污染地区的辐射强度约为安全标准的1000倍。专家估计随着放射性物质的衰变和环境的稀释,每过一年,辐射强度会下降一半。问从2011年开始,至少经过多少年,该地区的辐射强度才能达到安全标准?
解:设至少经过
年,该地区的辐射强度才能达到安全标准.
答:至少经过10年,该地区的辐射强度才能达到安全标准.
在R上单调递减,
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
