高中数学人教版A版必修一配套课件:第二章 2.1.1指数与指数幂的运算(一)(共24页PPT)
文档属性
| 名称 | 高中数学人教版A版必修一配套课件:第二章 2.1.1指数与指数幂的运算(一)(共24页PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 849.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 07:37:01 | ||
图片预览








文档简介
(共24张PPT)
2.1.1 指数与指数幂的运
算(一)
第二章
2.1
指数函数
1.理解n次方根、n次根式的概念;
2.正确运用根式运算性质化简、求值;
3.体会分类讨论思想、符号化思想的作用.
问题导学
题型探究
达标检测
学习目标
问题导学
新知探究
点点落实
知识点一 n次方根,n次根式
思考 若x2=3,这样的x有几个?它们叫作3的什么?怎么表示?
答案
一般地,有:(1)a的n次方根定义
如果
,那么x叫做a的n次方根,其中n>1,且n∈N
.
xn=a
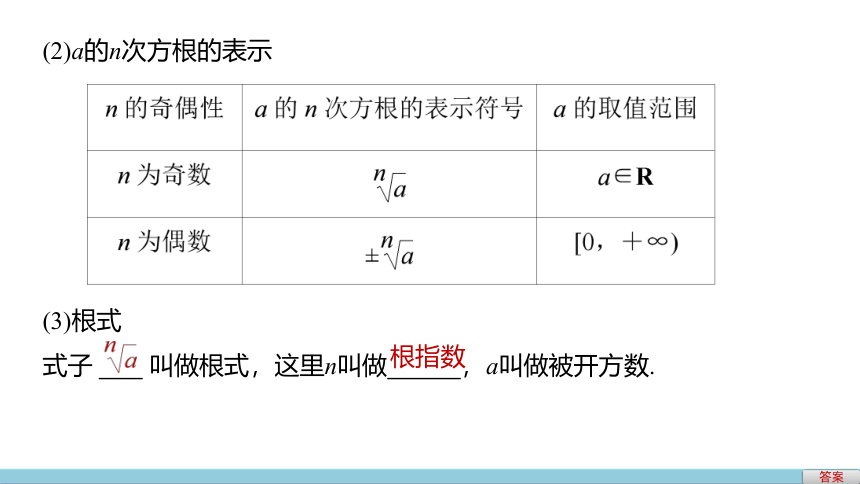
(2)a的n次方根的表示
答案
(3)根式
式子
叫做根式,这里n叫做
,a叫做被开方数.
根指数
知识点二 根式的性质
答案
答案
0
a
a
-a
返回
题型探究
重点难点
个个击破
类型一 根式的意义
解析答案
反思与感悟
反思与感悟
解析答案
∴a-1≥0,
∴a≥1.
类型二 利用根式的性质化简或求值
例2 化简:
解析答案
解析答案
解 由题意知a-1≥0,
即a≥1.
原式=a-1+|1-a|+1-a=a-1+a-1+1-a=a-1.
反思与感悟
反思与感悟
解析答案
跟踪训练2 求下列各式的值:
解析答案
类型三 有限制条件的根式的化简
解析答案
∵-3∴当-3原式=-(x-1)-(x+3)=-2x-2;
当1≤x<3时,原式=(x-1)-(x+3)=-4,
反思与感悟
反思与感悟
解析答案
跟踪训练3 例3中,若将“-3∵x≤-3,
∴x-1<0,x+3≤0,
∴原式=-(x-1)+(x+3)=4.
返回
1
2
3
达标检测
4
5
答案
B
1
2
3
4
5
答案
C
1
2
3
4
5
答案
A
1
2
3
4
5
答案
B
1
2
3
4
5
C
答案
规律与方法
返回
3.一个数到底有没有n次方根,我们一定先考虑被开方数到底是正数还是负数,还要分清n为奇数和偶数这两种情况.
2.1.1 指数与指数幂的运
算(一)
第二章
2.1
指数函数
1.理解n次方根、n次根式的概念;
2.正确运用根式运算性质化简、求值;
3.体会分类讨论思想、符号化思想的作用.
问题导学
题型探究
达标检测
学习目标
问题导学
新知探究
点点落实
知识点一 n次方根,n次根式
思考 若x2=3,这样的x有几个?它们叫作3的什么?怎么表示?
答案
一般地,有:(1)a的n次方根定义
如果
,那么x叫做a的n次方根,其中n>1,且n∈N
.
xn=a
(2)a的n次方根的表示
答案
(3)根式
式子
叫做根式,这里n叫做
,a叫做被开方数.
根指数
知识点二 根式的性质
答案
答案
0
a
a
-a
返回
题型探究
重点难点
个个击破
类型一 根式的意义
解析答案
反思与感悟
反思与感悟
解析答案
∴a-1≥0,
∴a≥1.
类型二 利用根式的性质化简或求值
例2 化简:
解析答案
解析答案
解 由题意知a-1≥0,
即a≥1.
原式=a-1+|1-a|+1-a=a-1+a-1+1-a=a-1.
反思与感悟
反思与感悟
解析答案
跟踪训练2 求下列各式的值:
解析答案
类型三 有限制条件的根式的化简
解析答案
∵-3
当1≤x<3时,原式=(x-1)-(x+3)=-4,
反思与感悟
反思与感悟
解析答案
跟踪训练3 例3中,若将“-3
∴x-1<0,x+3≤0,
∴原式=-(x-1)+(x+3)=4.
返回
1
2
3
达标检测
4
5
答案
B
1
2
3
4
5
答案
C
1
2
3
4
5
答案
A
1
2
3
4
5
答案
B
1
2
3
4
5
C
答案
规律与方法
返回
3.一个数到底有没有n次方根,我们一定先考虑被开方数到底是正数还是负数,还要分清n为奇数和偶数这两种情况.
