高中数学人教版A版必修一配套课件:第二章 章末复习课(共29页PPT)
文档属性
| 名称 | 高中数学人教版A版必修一配套课件:第二章 章末复习课(共29页PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 869.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 07:37:24 | ||
图片预览


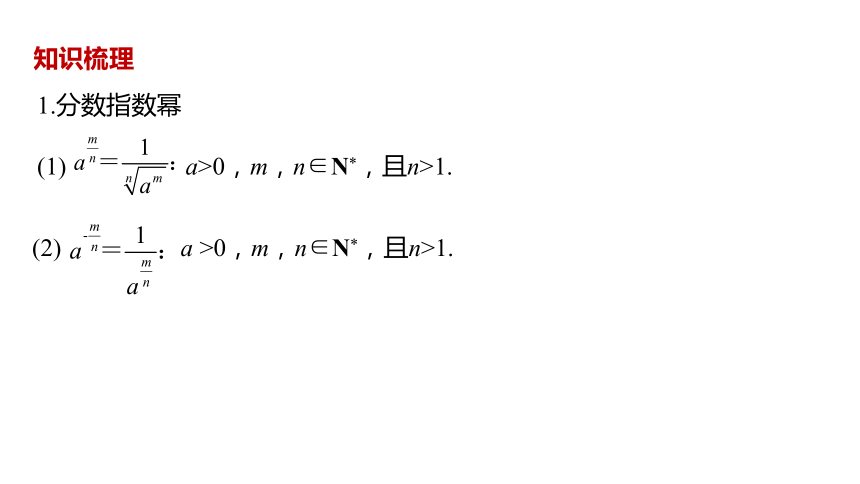




文档简介
(共29张PPT)
章末复习课
第二章
基本初等函数
(Ⅰ)
1.构建知识网络;
2.进一步熟练指数、对数运算,加深对公式成立条件的记忆;
3.以函数观点综合理解指数函数、对数函数、幂函数.
要点归纳
题型探究
达标检测
学习目标
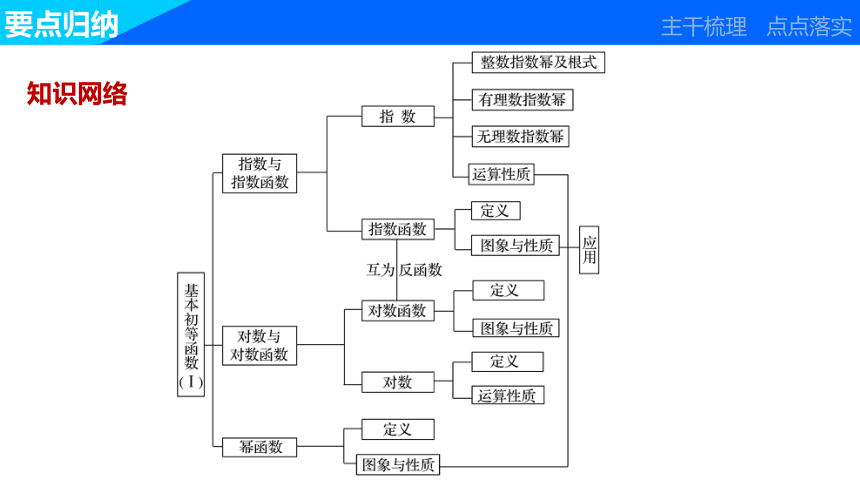
知识网络
要点归纳
主干梳理
点点落实
1.分数指数幂
知识梳理
(1)
a>0,m,n∈N
,且n>1.
(2)
a
>0,m,n∈N
,且n>1.
3.指数幂的运算性质
(1)ar·as=ar+s:a>0,r,s∈R.
(2)(ar)s=ars:a>0,r,s∈R.
(3)(ab)r=arbr:a>0,b>0,r∈R.
4.指数式与对数式的互化式
logaN=b?ab=N:a>0,a≠1,N>0.
返回
推论:
a>0,且a≠1,m,n>0,且m≠1,n≠1,b>0.
6.对数的四则运算法则
若a>0,a≠1,M>0,N>0,则
(1)
loga(MN)=logaM+logaN;
(3)logaMn=nlogaM(n∈R).
类型一 指数、对数的运算
题型探究
重点难点
个个击破
提炼化简方向:根式化分数指数幂,异底化同底.
化简技巧:分与合.
注意事项:变形过程中字母范围的变化.
解析答案
例1 化简:
解 原式
解 原式
解析答案
=log39-9=2-9=-7.
反思与感悟
(2)
反思与感悟
指数、对数的运算应遵循的原则
指数式的运算首先注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算,其次若出现分式则要注意分子、分母因式分解以达到约分的目的.对数运算首先注意公式应用过程中范围的变化,前后要等价,熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.
解析 ∵log32×log2(log327)=log32×log23
解析答案
∴原式
=21+4×27+1=111.
111
类型二 数的大小比较
例2 比较下列各组数的大小:
(1)27
,82;
解析答案
解 ∵82=(23)2=26,
由指数函数y=2x在R上单调递增知26<27即82<27.
(2)log20.4,log30.4,log40.4.
解析答案
解 ∵对数函数y=log0.4x在(0,+∞)上是减函数,
∴log0.44又幂函数y=x-1在(-∞,0)上是减函数,
即log20.4反思与感悟
反思与感悟
数的大小比较常用方法:
(1)比较两数(式)或几个数(式)大小问题是本章的一个重要题型,主要考查指数函数、对数函数、幂函数图象与性质的应用及差值比较法与商值比较法的应用.常用的方法有单调性法、图象法、中间搭桥法、作差法、作商法.
(2)当需要比较大小的两个实数均是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.
(3)比较多个数的大小时,先利用“0”和“1”作为分界点,即把它们分为“小于0”,“大于等于0小于等于1”,“大于1”三部分,再在各部分内利用函数的性质比较大小.
跟踪训练2 比较下列各组数的大小:
(1)log0.22,log0.049;
解析答案
又∵y=log0.2x在(0,+∞)上单调递减,
∴log0.22>log0.23,即log0.22>log0.049.
(2)a1.2,a1.3;
解析答案
解 ∵函数y=ax(a>0且a≠1),当底数a大于1时在R上是增函数;当底数a小于1时在R上是减函数,
而1.2<1.3,故当a>1时,有a1.2当0a1.3.
(3)0.213
,0.233.
解析答案
解 ∵y=x3在R上是增函数,
且0.21<0.23,∴0.213<0.233.
类型三 指数函数、对数函数、幂函数的综合应用
解析答案
反思与感悟
所以1+2x+a·4x>0在(-∞,1]上恒成立.
因为4x>0,
解析答案
反思与感悟
反思与感悟
反思与感悟
指数函数、对数函数、幂函数是使用频率非常高的基本初等函数,它们经过加、减、乘、除、复合、分段,构成我们以后研究的函数,使用时则通过换元、图象变换等手段化归为基本的指数函数、对数函数、幂函数来研究.
跟踪训练3 函数f(x)=loga(1-x)+loga(x+3)(0(1)求函数f(x)的定义域;
解析答案
解得-3返回
(2)若函数f(x)的最小值为-2,求a的值.
解析答案
解 函数可化为f(x)=loga[(1-x)(x+3)]=loga(-x2-2x+3)=loga[-(x+1)2+4].
∵-3∵01
2
3
达标检测
解析答案
A.1
B.2
C.3
D.0
4
5
B
解析答案
2.函数
的图象是( )
1
2
3
4
5
∴在第一象限增且上凸,又
为奇函数,过(1,1),故选B.
B
解析答案
A.都是增函数
B.都是减函数
C.f(x)是增函数,g(x)是减函数
D.f(x)是减函数,g(x)是增函数
1
2
3
4
5
x∈(0,+∞)时
为减函数,所以在(-∞,0)上为增函数.
D
解析答案
A.P<Q<R
B.Q<R<P
C.Q<P<R
D.R<Q<P
1
2
3
4
5
由函数y=2x在R上是增函数知,
所以P>R>Q.
B
解析答案
5.函数
的值域为( )
1
2
3
4
5
C
返回
规律与方法
1.函数是高中数学极为重要的内容,函数思想和函数方法贯穿整个高中数学的过程,对本章的考查是以基本函数形式出现的综合题和应用题,一直是常考不衰的热点问题.
2.从考查角度看,指数函数、对数函数概念的考查以基本概念与基本计算为主;对图象的考查重在考查平移变换、对称变换以及利用数形结合的思想方法解决数学问题的能力;对幂函数的考查将会从概念、图象、性质等方面来考查.
章末复习课
第二章
基本初等函数
(Ⅰ)
1.构建知识网络;
2.进一步熟练指数、对数运算,加深对公式成立条件的记忆;
3.以函数观点综合理解指数函数、对数函数、幂函数.
要点归纳
题型探究
达标检测
学习目标
知识网络
要点归纳
主干梳理
点点落实
1.分数指数幂
知识梳理
(1)
a>0,m,n∈N
,且n>1.
(2)
a
>0,m,n∈N
,且n>1.
3.指数幂的运算性质
(1)ar·as=ar+s:a>0,r,s∈R.
(2)(ar)s=ars:a>0,r,s∈R.
(3)(ab)r=arbr:a>0,b>0,r∈R.
4.指数式与对数式的互化式
logaN=b?ab=N:a>0,a≠1,N>0.
返回
推论:
a>0,且a≠1,m,n>0,且m≠1,n≠1,b>0.
6.对数的四则运算法则
若a>0,a≠1,M>0,N>0,则
(1)
loga(MN)=logaM+logaN;
(3)logaMn=nlogaM(n∈R).
类型一 指数、对数的运算
题型探究
重点难点
个个击破
提炼化简方向:根式化分数指数幂,异底化同底.
化简技巧:分与合.
注意事项:变形过程中字母范围的变化.
解析答案
例1 化简:
解 原式
解 原式
解析答案
=log39-9=2-9=-7.
反思与感悟
(2)
反思与感悟
指数、对数的运算应遵循的原则
指数式的运算首先注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算,其次若出现分式则要注意分子、分母因式分解以达到约分的目的.对数运算首先注意公式应用过程中范围的变化,前后要等价,熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.
解析 ∵log32×log2(log327)=log32×log23
解析答案
∴原式
=21+4×27+1=111.
111
类型二 数的大小比较
例2 比较下列各组数的大小:
(1)27
,82;
解析答案
解 ∵82=(23)2=26,
由指数函数y=2x在R上单调递增知26<27即82<27.
(2)log20.4,log30.4,log40.4.
解析答案
解 ∵对数函数y=log0.4x在(0,+∞)上是减函数,
∴log0.44
即log20.4
反思与感悟
数的大小比较常用方法:
(1)比较两数(式)或几个数(式)大小问题是本章的一个重要题型,主要考查指数函数、对数函数、幂函数图象与性质的应用及差值比较法与商值比较法的应用.常用的方法有单调性法、图象法、中间搭桥法、作差法、作商法.
(2)当需要比较大小的两个实数均是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.
(3)比较多个数的大小时,先利用“0”和“1”作为分界点,即把它们分为“小于0”,“大于等于0小于等于1”,“大于1”三部分,再在各部分内利用函数的性质比较大小.
跟踪训练2 比较下列各组数的大小:
(1)log0.22,log0.049;
解析答案
又∵y=log0.2x在(0,+∞)上单调递减,
∴log0.22>log0.23,即log0.22>log0.049.
(2)a1.2,a1.3;
解析答案
解 ∵函数y=ax(a>0且a≠1),当底数a大于1时在R上是增函数;当底数a小于1时在R上是减函数,
而1.2<1.3,故当a>1时,有a1.2
(3)0.213
,0.233.
解析答案
解 ∵y=x3在R上是增函数,
且0.21<0.23,∴0.213<0.233.
类型三 指数函数、对数函数、幂函数的综合应用
解析答案
反思与感悟
所以1+2x+a·4x>0在(-∞,1]上恒成立.
因为4x>0,
解析答案
反思与感悟
反思与感悟
反思与感悟
指数函数、对数函数、幂函数是使用频率非常高的基本初等函数,它们经过加、减、乘、除、复合、分段,构成我们以后研究的函数,使用时则通过换元、图象变换等手段化归为基本的指数函数、对数函数、幂函数来研究.
跟踪训练3 函数f(x)=loga(1-x)+loga(x+3)(0
解析答案
解得-3
(2)若函数f(x)的最小值为-2,求a的值.
解析答案
解 函数可化为f(x)=loga[(1-x)(x+3)]=loga(-x2-2x+3)=loga[-(x+1)2+4].
∵-3
2
3
达标检测
解析答案
A.1
B.2
C.3
D.0
4
5
B
解析答案
2.函数
的图象是( )
1
2
3
4
5
∴在第一象限增且上凸,又
为奇函数,过(1,1),故选B.
B
解析答案
A.都是增函数
B.都是减函数
C.f(x)是增函数,g(x)是减函数
D.f(x)是减函数,g(x)是增函数
1
2
3
4
5
x∈(0,+∞)时
为减函数,所以在(-∞,0)上为增函数.
D
解析答案
A.P<Q<R
B.Q<R<P
C.Q<P<R
D.R<Q<P
1
2
3
4
5
由函数y=2x在R上是增函数知,
所以P>R>Q.
B
解析答案
5.函数
的值域为( )
1
2
3
4
5
C
返回
规律与方法
1.函数是高中数学极为重要的内容,函数思想和函数方法贯穿整个高中数学的过程,对本章的考查是以基本函数形式出现的综合题和应用题,一直是常考不衰的热点问题.
2.从考查角度看,指数函数、对数函数概念的考查以基本概念与基本计算为主;对图象的考查重在考查平移变换、对称变换以及利用数形结合的思想方法解决数学问题的能力;对幂函数的考查将会从概念、图象、性质等方面来考查.
