人教版九年级数学上册25.3利用频率估计概率课件(共26张PPT)
文档属性
| 名称 | 人教版九年级数学上册25.3利用频率估计概率课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
1.学会根据问题的特点,用统计来估计事件发生的概率,培养分析问题,解决问题的能力.
2.通过对问题的分析,理解用频率来估计概率的方法,渗透转化和估算的思想方法.
重点:通过对事件发生的频率的分析来估计事件发生的概率.
难点:大量重复试验得到频率的稳定值的分析.
一、频率与概率的区别与联系
(1)区别:频率是随着试验次数的改变而改变,即频率是随机的,而试验前是不确定的,而概率是一个确定的常数,是客观存在的,与试验次数无关,是随机事件自身的一个属性。
(2)联系:在相同的条件下,随着试验次数的增加,随机事件发生的频率会在某个常数附近摆动并趋于稳定,所以可用频率作为概率的近似值,当试验次数越来越多时频率向概率靠近,概率是频率的近似值。
二、频率与概率应注意的问题
①求一个事件的概率的基本方法是做大量的重复试验。
②只有当频率在某个常数附近摆动时,这个常数才叫做事件的概率。
③概率是频率的稳定值,而频率是概率的近似值。
④概率反应了随机事件发生的可能性的大小。
⑤概率的值越接近1表明事件发生的可能性越大,反过来值越接近0,则事件发生的可能性越小。
频率
固定
p
探究:投掷硬币时,国徽朝上的可能性有多大?
抛掷次数(n)
2048
4040
12000
30000
24000
72088
正面朝上数(m)
1061
2048
6019
14984
12012
36124
频率(m/n)
0.518
0.506
0.501
0.4996
0.5005
0.5011
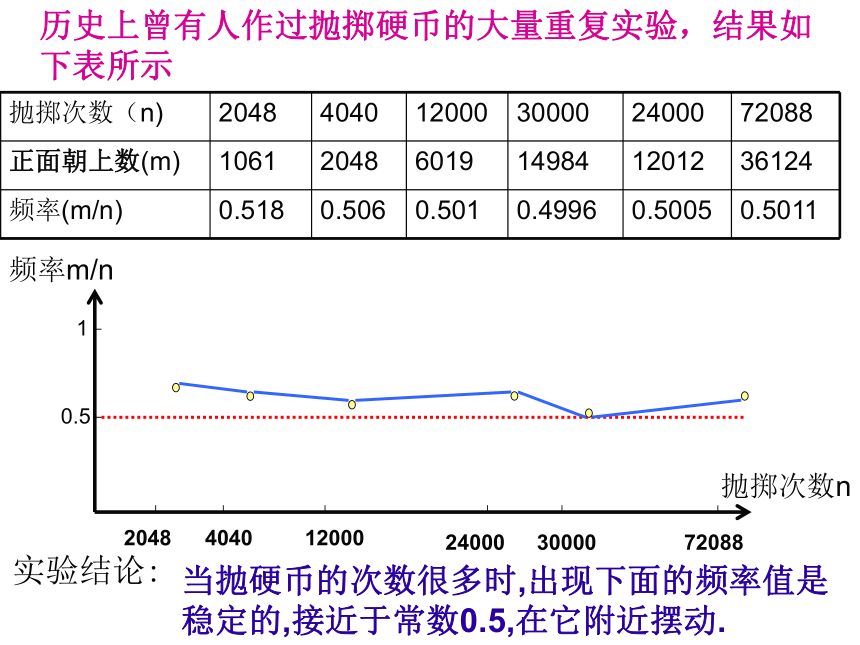
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
实验结论:
当抛硬币的次数很多时,出现下面的频率值是
稳定的,接近于常数0.5,在它附近摆动.
我们知道,当抛掷一枚硬币时,要么出现正面,要么出现反面,
它们是随机的.通过上面的试验,我们发现在大量试验中出现正
面的可能为0.5,那么出现反面的可能为多少呢?
这就是为什么我们在抛一次硬币时,说出现正面的
可能为0.5,出现反面的可能为0.5.
出现反面的可能也为0.5
随机事件在一次试验中是否
发生虽然不能事先确定,但是在
大量重复试验的情况下,它的发
生呈现出一定的规律性.出现的频率值接近于常数.
随机事件及其概率
某批乒乓球产品质量检查结果表:
当抽查的球数很多时,抽到优等品的频率
接近于常数0.95,在它附近摆动。
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率
2000
1000
500
200
100
50
1902
954
470
194
92
45
优等品数
抽取球数
很多
常数
某种油菜籽在相同条件下的发芽试验结果表:
当试验的油菜籽的粒数很多时,油菜籽发芽
的频率
接近于常数0.9,在它附近摆动。
很多
常数
随机事件及其概率
事件
的概率的定义:
一般地,在大量重复进行同一试验时,事件
发生的频率
(n为实验的次数,m是事件发生的频数)总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件
的概率,记做
.
由定义可知:
(1)求一个事件的概率的基本方法是通过大量的重复试验;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0.因此
.
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A
的概率;
可以看到事件发生的可能性越大概率就越接近1;反之,
事件发生的可能性越小概率就越接近0
知识点一
概率的意义
B
B
知识点一
概率的意义
知识点二
用频率去估计概率
D
A
例1:有一箱规格相同的红、黄两种颜色的小塑料球共1000个.为了估计这两种颜色的球各有多少个,小明将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到红球的频率约为0.6,据此可以估计红球的个数约为________.
600
解析:
答案:
600.
因为多次重复上述过程后,发现摸到红球的频率约为0.6,所以红球所占的百分比也就是60%,根据总数可求出红球个数.
解:
∵摸到红球的频率约为0.6,
∴红球所占的百分比是60%.
∴1000×60%=600.
解析:
数出这个句子中所有字母的个数和字母“o”出现的频数,由频率=频数÷总个数计算.
例2:“Welcomc
to
Senior
High
School.”在这段句子的所有英文字母中,字母O出现的频率是_____.
解:
在“Welcomc
to
Senior
High
School.”这个句子中:有25个字母,其中有5个“o”,故字母“o”出现的频率为5÷25=0.2.
故答案为0.2.
0.2
例3:研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色
无记号
有记号
红色
黄色
红色
黄色
摸到的次数
18
28
2
2
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
解:
(1)由题意可知,50次摸球实验活动中,出现红球20次,黄球30次,
∴红球所占百分比为20÷50=40%,
黄球所占百分比为30÷50=60%,
答:红球占40%,黄球占60%;
(2)由题意可知,50次摸球实验活动中,出现有记号的球4次,
∴红球数为100×40%=40,
答:盒中红球有40个.
∴总球数为
×8=100,
D
D
解:
(1)树状图
y=-x+1,y=-x+2,y=x-1,y=x+2,y=2x-1,y=2x+1
(2)
P(一次函数图象不经过第四象限)=
一般地,当试验的可能结果有很多且各种可能结
果发生的可能性相等时,
可以用
的方式得出
概率.当试验的所有可能结果不是有限个,或各种可能
结果发生的可能性不相等时,常常是通过统计频率来
估计概率,即在同样条件下,大量重复试验所得到的随
机事件发生的频率的稳定值来估计这个事件发生的
概率.
1.学会根据问题的特点,用统计来估计事件发生的概率,培养分析问题,解决问题的能力.
2.通过对问题的分析,理解用频率来估计概率的方法,渗透转化和估算的思想方法.
重点:通过对事件发生的频率的分析来估计事件发生的概率.
难点:大量重复试验得到频率的稳定值的分析.
一、频率与概率的区别与联系
(1)区别:频率是随着试验次数的改变而改变,即频率是随机的,而试验前是不确定的,而概率是一个确定的常数,是客观存在的,与试验次数无关,是随机事件自身的一个属性。
(2)联系:在相同的条件下,随着试验次数的增加,随机事件发生的频率会在某个常数附近摆动并趋于稳定,所以可用频率作为概率的近似值,当试验次数越来越多时频率向概率靠近,概率是频率的近似值。
二、频率与概率应注意的问题
①求一个事件的概率的基本方法是做大量的重复试验。
②只有当频率在某个常数附近摆动时,这个常数才叫做事件的概率。
③概率是频率的稳定值,而频率是概率的近似值。
④概率反应了随机事件发生的可能性的大小。
⑤概率的值越接近1表明事件发生的可能性越大,反过来值越接近0,则事件发生的可能性越小。
频率
固定
p
探究:投掷硬币时,国徽朝上的可能性有多大?
抛掷次数(n)
2048
4040
12000
30000
24000
72088
正面朝上数(m)
1061
2048
6019
14984
12012
36124
频率(m/n)
0.518
0.506
0.501
0.4996
0.5005
0.5011
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
实验结论:
当抛硬币的次数很多时,出现下面的频率值是
稳定的,接近于常数0.5,在它附近摆动.
我们知道,当抛掷一枚硬币时,要么出现正面,要么出现反面,
它们是随机的.通过上面的试验,我们发现在大量试验中出现正
面的可能为0.5,那么出现反面的可能为多少呢?
这就是为什么我们在抛一次硬币时,说出现正面的
可能为0.5,出现反面的可能为0.5.
出现反面的可能也为0.5
随机事件在一次试验中是否
发生虽然不能事先确定,但是在
大量重复试验的情况下,它的发
生呈现出一定的规律性.出现的频率值接近于常数.
随机事件及其概率
某批乒乓球产品质量检查结果表:
当抽查的球数很多时,抽到优等品的频率
接近于常数0.95,在它附近摆动。
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率
2000
1000
500
200
100
50
1902
954
470
194
92
45
优等品数
抽取球数
很多
常数
某种油菜籽在相同条件下的发芽试验结果表:
当试验的油菜籽的粒数很多时,油菜籽发芽
的频率
接近于常数0.9,在它附近摆动。
很多
常数
随机事件及其概率
事件
的概率的定义:
一般地,在大量重复进行同一试验时,事件
发生的频率
(n为实验的次数,m是事件发生的频数)总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件
的概率,记做
.
由定义可知:
(1)求一个事件的概率的基本方法是通过大量的重复试验;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0.因此
.
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A
的概率;
可以看到事件发生的可能性越大概率就越接近1;反之,
事件发生的可能性越小概率就越接近0
知识点一
概率的意义
B
B
知识点一
概率的意义
知识点二
用频率去估计概率
D
A
例1:有一箱规格相同的红、黄两种颜色的小塑料球共1000个.为了估计这两种颜色的球各有多少个,小明将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到红球的频率约为0.6,据此可以估计红球的个数约为________.
600
解析:
答案:
600.
因为多次重复上述过程后,发现摸到红球的频率约为0.6,所以红球所占的百分比也就是60%,根据总数可求出红球个数.
解:
∵摸到红球的频率约为0.6,
∴红球所占的百分比是60%.
∴1000×60%=600.
解析:
数出这个句子中所有字母的个数和字母“o”出现的频数,由频率=频数÷总个数计算.
例2:“Welcomc
to
Senior
High
School.”在这段句子的所有英文字母中,字母O出现的频率是_____.
解:
在“Welcomc
to
Senior
High
School.”这个句子中:有25个字母,其中有5个“o”,故字母“o”出现的频率为5÷25=0.2.
故答案为0.2.
0.2
例3:研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色
无记号
有记号
红色
黄色
红色
黄色
摸到的次数
18
28
2
2
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
解:
(1)由题意可知,50次摸球实验活动中,出现红球20次,黄球30次,
∴红球所占百分比为20÷50=40%,
黄球所占百分比为30÷50=60%,
答:红球占40%,黄球占60%;
(2)由题意可知,50次摸球实验活动中,出现有记号的球4次,
∴红球数为100×40%=40,
答:盒中红球有40个.
∴总球数为
×8=100,
D
D
解:
(1)树状图
y=-x+1,y=-x+2,y=x-1,y=x+2,y=2x-1,y=2x+1
(2)
P(一次函数图象不经过第四象限)=
一般地,当试验的可能结果有很多且各种可能结
果发生的可能性相等时,
可以用
的方式得出
概率.当试验的所有可能结果不是有限个,或各种可能
结果发生的可能性不相等时,常常是通过统计频率来
估计概率,即在同样条件下,大量重复试验所得到的随
机事件发生的频率的稳定值来估计这个事件发生的
概率.
同课章节目录
