人教版数学八年级上册13.1.2 线段的垂直平分线的性质课件(共29张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.1.2 线段的垂直平分线的性质课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 847.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
学习目标
1.理解线段垂直平分线的性质和判定.
2.能运用线段垂直平分线的性质和判定解决
实际问题.
3.会用尺规经过已知直线外一点作这条直线
的垂线,了解作图的道理.
4.能用尺规作线段的垂直平分线.
轴对称图形
轴对称
区别
联系
1、对两个图形而言
2、指两个图形的相互关系
3、只有一条对称轴
1、对一个图形而言
2、指一个图形的特殊形状
3、至少有一条对称轴
1、沿某条直线对折后,直线两旁的部分都能重合;
2、若将成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;若把轴对称图形沿对称轴看成两个图形,那么这两个图形关于这条对称轴成轴对称.
3、都有对称轴
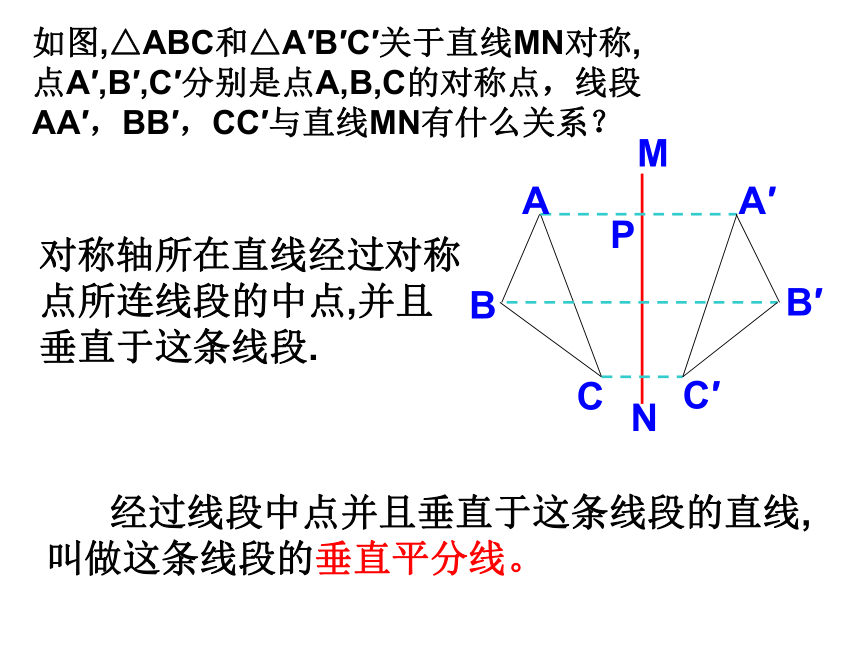
如图,△ABC和△A′B′C′关于直线MN对称,
点A′,B′,C′分别是点A,B,C的对称点,线段
AA′,BB′,CC′与直线MN有什么关系?
B
A
A′
B′
C
C′
M
P
N
对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
如图,△ABC和△A′B′C′关于直线MN对称,
点A′,B′,C′分别是点A,B,C的对称点,线段
AA′,BB′,CC′与直线MN有什么关系?
B
A
A′
B′
C
C′
M
P
N
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
也就是说对称点的连线被对称轴垂直平分。
成轴对称的两个图形的性质:
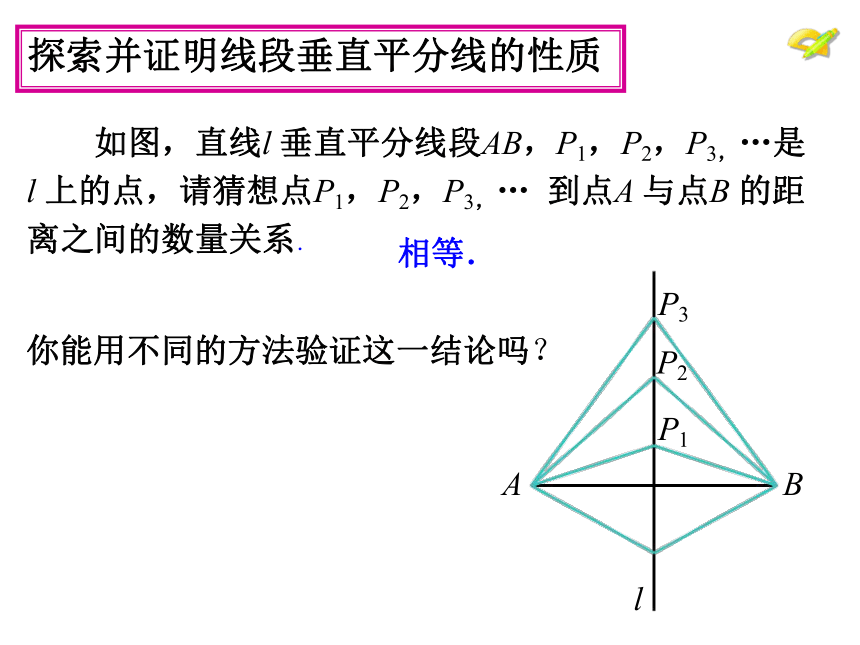
你能用不同的方法验证这一结论吗?
探索并证明线段垂直平分线的性质
如图,直线l
垂直平分线段AB,P1,P2,P3,…是
l
上的点,请猜想点P1,P2,P3,…
到点A
与点B
的距
离之间的数量关系.
相等.
A
B
l
P1
P2
P3
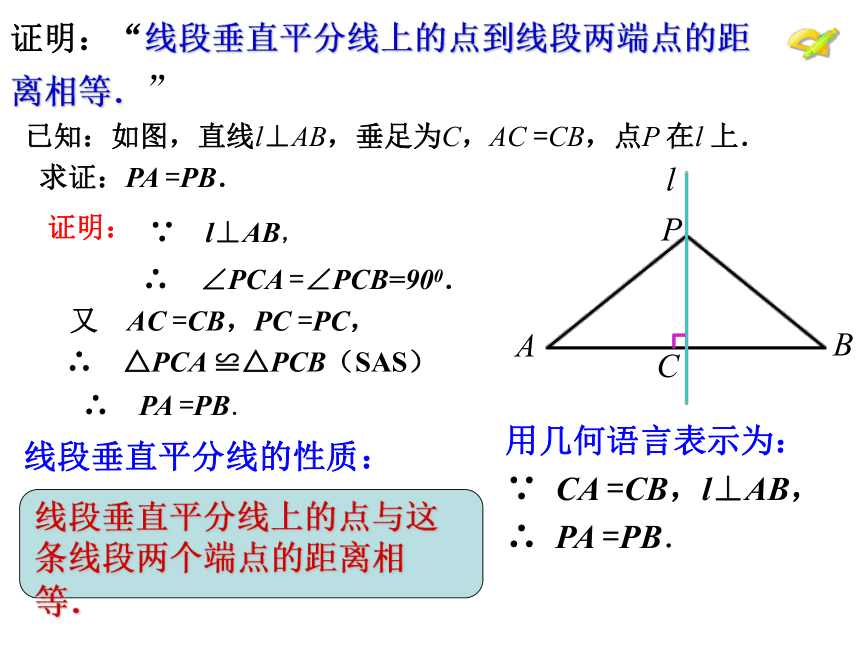
用几何语言表示为:
∵
CA
=CB,l⊥AB,
∴
PA
=PB.
证明:
A
B
P
C
l
线段垂直平分线的性质:
已知:如图,直线l⊥AB,垂足为C,AC
=CB,点P
在l
上.
求证:PA
=PB.
证明:“线段垂直平分线上的点到线段两端点的距
离相等.”
∵ l⊥AB,
∴
∠PCA
=∠PCB=900.
又
AC
=CB,PC
=PC,
∴
△PCA
≌△PCB(SAS)
∴
PA
=PB.
线段垂直平分线上的点与这条线段两个端点的距离相等.
8
课堂练习
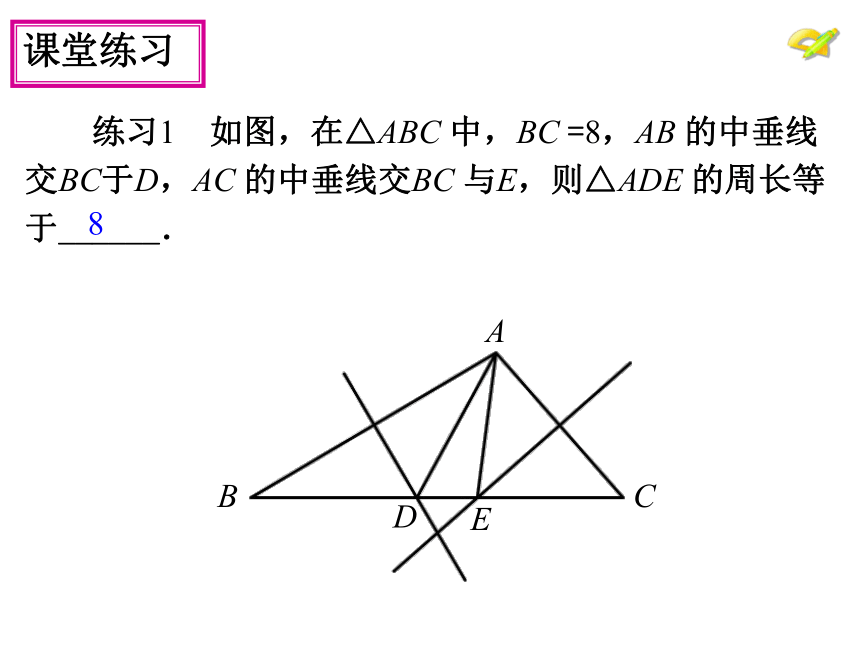
练习1 如图,在△ABC
中,BC
=8,AB
的中垂线
交BC于D,AC
的中垂线交BC
与E,则△ADE
的周长等
于______.
A
B
C
D
E
P
A
B
C
已知:如图,PA
=PB.
求证:点P
在线段AB
的垂直平分线上.
证明:
如图作PC⊥AB
则∠PCA
=∠PCB
=90°.
在Rt△PCA
和Rt△PCB
中,
∴
Rt△PCA
≌Rt△PCB(HL).
∴
AC
=BC.
又
PC⊥AB,
∴
点P
在线段AB
的垂直平分线上
PA
=PB,
PC
=PC,
反过来,如果PA
=PB,那么点P
是否在线段AB
的垂直平分线上呢?
点P
在线段AB
的垂直平分线上.
探索并证明线段垂直平分线的判定
用几何语言表示为:
P
A
B
C
线段垂直平分线的判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∵ PA
=PB,
∴ 点P
在AB
的垂直平分线上.
这些点能组成什么几何图形?
你能再找一些到线段AB
两端点的距离相等的点吗?
能找到多少个到线段AB
两端点距离相等的点?
在线段AB
的垂直平分线l
上的
点与A,B
的距离都相等;反过来,
与A,B
的距离相等的点都在直线l
上,所以直线l
可以看成与两点A、
B
的距离相等的所有点的集合.
P
A
B
C
解:∵ AD⊥BC,BD
=DC
∴ AD
是BC
的垂直平分线
∴ AB
=AC
∵ 点C
在AE
的垂直平分线上
∴ AC
=CE.
∴ AB
=AC
=CE
课堂练习P62(1)
2 如图,AD⊥BC,BD
=DC,点C
在AE
的垂直平分线上,AB,AC,CE
的长度有什么关系?AB+BD与DE
有什么关系?
A
B
C
D
E
∵ AB
=CE,BD
=DC,∴ AB
+BD
=CD
+CE.
即 AB
+BD
=DE
.
解:∵ AB
=AC,
∴ 点A
在BC
的垂直平分线.
∵ MB
=MC,
∵ 点M
在BC
的垂直平分线上∴ 直线AM
是线段BC
的垂直
平分线.
课堂练习P62(2)
练习3 如图,AB
=AC,MB
=MC.直线AM
是线段BC
的垂直平分线吗?
A
B
C
D
M
(1)任意取一点K
,使点K与点C
在直线AB两旁.
尺规作图
经过已知直线外一点作这条直线的垂线。
(2)以点C为圆心,CK为半径作弧,交AB于点D和点E.
(4)作直线CF,直线CF
就是所求作的垂线。
C
A
B
K
F
D
E
已知:直线AB和AB外一点C
求作:AB的垂线,使它经过点C.
做法:
(3)分别以点D和点E为圆心,大于
的长为半径作弧,两弧相交于点F.
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
(4)经过已知直线外一点作这条直线的垂线.
那么利用尺规还能解决什么作图问题呢?
我们已能用尺规完成:
作线段的垂直平分线
如果两个图形成轴对称,其对称轴是任何一对对应点所连线段的垂直平分线.因此,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
如果两个图形成轴对称,怎样作出图形的对称轴?
作线段的垂直平分线
例1 如图,点A
和点B
关于某条直线成轴对称,
你能作出这条直线吗?
A
B
这种作法的依据是什么?
作线段的垂直平分线
A
B
C
D
作法:
(1)分别以点A,B
为圆心,以大于
AB的长为半径
作弧,两弧相交于C,D
两点;
(2)作直线CD.
CD
就是所求作的直线.
这种作图方法还有哪些作用?
确定线段的中点.
五角星的对称轴有什么特点?
你能作出这个五角星的其他对称轴吗?它共有几条
对称轴?
相交于一点.
如图中的五角星,请作出它的一条对称轴.
课堂练习
练习1 作出下列图形的一条对称轴,和同学比较
一下,你们作出的对称轴一样吗?
课堂练习
练习2 如图,角是轴对称图形吗?如果是,它的
对称轴是什么?
课堂练习
练习3 如图,与图形A
成轴对称的是哪个图形?
画出它的对称轴.
A
B
C
D
已知:
△ABC中,边AB、
BC的垂直平分线交于点P。求证:PA=PB=PC.
P
A
B
C
结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等。
拓展:
如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。
如图,八(1)班与八(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由。?
M
N
B
C
A
P
3、如图PA=PB,则直线MN是线段AB的垂直平分线。
结论:
线段垂直平分线上的点
与这条线段两个端点的距离相等。
反之,与线段两个端点的距离相等的点
在这条线段垂直平分线上。
所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合。
课堂小结
12.3角的平分线
O
D
E
A
B
P
C
定理1
在角的平分线上的点到这个角的两边的距离相等。
定理2
到一个角的两边的距离相等的点,在这个角的平分线上。
角的平分线是到角的两边距离相等的所有点的集合
13.1.2
线段的垂直平分线
定
理
线段垂直平分线上的点和这条线段两个端点的距离相等。
逆定理
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合
A
B
M
N
P
点的集合是一条射线
点的集合是一条直线
学习目标
1.理解线段垂直平分线的性质和判定.
2.能运用线段垂直平分线的性质和判定解决
实际问题.
3.会用尺规经过已知直线外一点作这条直线
的垂线,了解作图的道理.
4.能用尺规作线段的垂直平分线.
轴对称图形
轴对称
区别
联系
1、对两个图形而言
2、指两个图形的相互关系
3、只有一条对称轴
1、对一个图形而言
2、指一个图形的特殊形状
3、至少有一条对称轴
1、沿某条直线对折后,直线两旁的部分都能重合;
2、若将成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;若把轴对称图形沿对称轴看成两个图形,那么这两个图形关于这条对称轴成轴对称.
3、都有对称轴
如图,△ABC和△A′B′C′关于直线MN对称,
点A′,B′,C′分别是点A,B,C的对称点,线段
AA′,BB′,CC′与直线MN有什么关系?
B
A
A′
B′
C
C′
M
P
N
对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
如图,△ABC和△A′B′C′关于直线MN对称,
点A′,B′,C′分别是点A,B,C的对称点,线段
AA′,BB′,CC′与直线MN有什么关系?
B
A
A′
B′
C
C′
M
P
N
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
也就是说对称点的连线被对称轴垂直平分。
成轴对称的两个图形的性质:
你能用不同的方法验证这一结论吗?
探索并证明线段垂直平分线的性质
如图,直线l
垂直平分线段AB,P1,P2,P3,…是
l
上的点,请猜想点P1,P2,P3,…
到点A
与点B
的距
离之间的数量关系.
相等.
A
B
l
P1
P2
P3
用几何语言表示为:
∵
CA
=CB,l⊥AB,
∴
PA
=PB.
证明:
A
B
P
C
l
线段垂直平分线的性质:
已知:如图,直线l⊥AB,垂足为C,AC
=CB,点P
在l
上.
求证:PA
=PB.
证明:“线段垂直平分线上的点到线段两端点的距
离相等.”
∵ l⊥AB,
∴
∠PCA
=∠PCB=900.
又
AC
=CB,PC
=PC,
∴
△PCA
≌△PCB(SAS)
∴
PA
=PB.
线段垂直平分线上的点与这条线段两个端点的距离相等.
8
课堂练习
练习1 如图,在△ABC
中,BC
=8,AB
的中垂线
交BC于D,AC
的中垂线交BC
与E,则△ADE
的周长等
于______.
A
B
C
D
E
P
A
B
C
已知:如图,PA
=PB.
求证:点P
在线段AB
的垂直平分线上.
证明:
如图作PC⊥AB
则∠PCA
=∠PCB
=90°.
在Rt△PCA
和Rt△PCB
中,
∴
Rt△PCA
≌Rt△PCB(HL).
∴
AC
=BC.
又
PC⊥AB,
∴
点P
在线段AB
的垂直平分线上
PA
=PB,
PC
=PC,
反过来,如果PA
=PB,那么点P
是否在线段AB
的垂直平分线上呢?
点P
在线段AB
的垂直平分线上.
探索并证明线段垂直平分线的判定
用几何语言表示为:
P
A
B
C
线段垂直平分线的判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∵ PA
=PB,
∴ 点P
在AB
的垂直平分线上.
这些点能组成什么几何图形?
你能再找一些到线段AB
两端点的距离相等的点吗?
能找到多少个到线段AB
两端点距离相等的点?
在线段AB
的垂直平分线l
上的
点与A,B
的距离都相等;反过来,
与A,B
的距离相等的点都在直线l
上,所以直线l
可以看成与两点A、
B
的距离相等的所有点的集合.
P
A
B
C
解:∵ AD⊥BC,BD
=DC
∴ AD
是BC
的垂直平分线
∴ AB
=AC
∵ 点C
在AE
的垂直平分线上
∴ AC
=CE.
∴ AB
=AC
=CE
课堂练习P62(1)
2 如图,AD⊥BC,BD
=DC,点C
在AE
的垂直平分线上,AB,AC,CE
的长度有什么关系?AB+BD与DE
有什么关系?
A
B
C
D
E
∵ AB
=CE,BD
=DC,∴ AB
+BD
=CD
+CE.
即 AB
+BD
=DE
.
解:∵ AB
=AC,
∴ 点A
在BC
的垂直平分线.
∵ MB
=MC,
∵ 点M
在BC
的垂直平分线上∴ 直线AM
是线段BC
的垂直
平分线.
课堂练习P62(2)
练习3 如图,AB
=AC,MB
=MC.直线AM
是线段BC
的垂直平分线吗?
A
B
C
D
M
(1)任意取一点K
,使点K与点C
在直线AB两旁.
尺规作图
经过已知直线外一点作这条直线的垂线。
(2)以点C为圆心,CK为半径作弧,交AB于点D和点E.
(4)作直线CF,直线CF
就是所求作的垂线。
C
A
B
K
F
D
E
已知:直线AB和AB外一点C
求作:AB的垂线,使它经过点C.
做法:
(3)分别以点D和点E为圆心,大于
的长为半径作弧,两弧相交于点F.
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
(4)经过已知直线外一点作这条直线的垂线.
那么利用尺规还能解决什么作图问题呢?
我们已能用尺规完成:
作线段的垂直平分线
如果两个图形成轴对称,其对称轴是任何一对对应点所连线段的垂直平分线.因此,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
如果两个图形成轴对称,怎样作出图形的对称轴?
作线段的垂直平分线
例1 如图,点A
和点B
关于某条直线成轴对称,
你能作出这条直线吗?
A
B
这种作法的依据是什么?
作线段的垂直平分线
A
B
C
D
作法:
(1)分别以点A,B
为圆心,以大于
AB的长为半径
作弧,两弧相交于C,D
两点;
(2)作直线CD.
CD
就是所求作的直线.
这种作图方法还有哪些作用?
确定线段的中点.
五角星的对称轴有什么特点?
你能作出这个五角星的其他对称轴吗?它共有几条
对称轴?
相交于一点.
如图中的五角星,请作出它的一条对称轴.
课堂练习
练习1 作出下列图形的一条对称轴,和同学比较
一下,你们作出的对称轴一样吗?
课堂练习
练习2 如图,角是轴对称图形吗?如果是,它的
对称轴是什么?
课堂练习
练习3 如图,与图形A
成轴对称的是哪个图形?
画出它的对称轴.
A
B
C
D
已知:
△ABC中,边AB、
BC的垂直平分线交于点P。求证:PA=PB=PC.
P
A
B
C
结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等。
拓展:
如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。
如图,八(1)班与八(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由。?
M
N
B
C
A
P
3、如图PA=PB,则直线MN是线段AB的垂直平分线。
结论:
线段垂直平分线上的点
与这条线段两个端点的距离相等。
反之,与线段两个端点的距离相等的点
在这条线段垂直平分线上。
所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合。
课堂小结
12.3角的平分线
O
D
E
A
B
P
C
定理1
在角的平分线上的点到这个角的两边的距离相等。
定理2
到一个角的两边的距离相等的点,在这个角的平分线上。
角的平分线是到角的两边距离相等的所有点的集合
13.1.2
线段的垂直平分线
定
理
线段垂直平分线上的点和这条线段两个端点的距离相等。
逆定理
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合
A
B
M
N
P
点的集合是一条射线
点的集合是一条直线
