11.3 多边形及其内角和-2020-2021数学八上同步课堂帮帮帮(含解析)
文档属性
| 名称 | 11.3 多边形及其内角和-2020-2021数学八上同步课堂帮帮帮(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
11.3 多边形及其内角和
目标梳理
学习目标 重点难点
1.了解多边形及其相关概念,理解正多边形及其概念。 2.学会判断一个图形是否是凸多边形
3.理解多边形的对角线的概念
4.能通过不同的方法探索多边形的内角和与外角和公式
5.会应用多边形的内角和与外角和公式进行有关计算
6.通过多边形内角和计算公式的推导,培养学生探索与归纳能力 1.重点:多边形、正多边形的定义及相关概念;多边形的内角和与外角和公式
2.难点:会求多边形的对角线的条数;多边形的内角和公式的推导
知识梳理
一、多边形及其相关概念
1.多边形:在平面内,由一些线段首尾顺次相接组成的___________叫做多边形.多边形按组成它的线段的条数分成三角形、四边形、五边形……,如果一个多边形由条线段组成,那么这个多边形就叫做边形.www.21-cn-jy.com
2.相关概念:①多边形相邻_??¤è???????????è§?_叫做它的___________.②多边形的边与它的邻边的延长线组成的角叫做多边形的___________.③连接多边形不相邻的两个顶点的线段,叫做多边形的___________.【来源:21·世纪·教育·网】
二、多边形的对角线
1.定义:多边形的对角线:连接多边形不相邻的两个顶点的__________,叫做多边形的对角线.
2.规律总结:
①从n边形的一个顶点出发可以引(n-3)条对角线,将n边形分成(n-2)个三角形.
②n边形共有条对角线.
三、凸多边形与正多边形
1.凸多边形:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的___________,那么这个多边形叫做凸多边形.2·1·c·n·j·y
2.正多边形:各个角都相等,各条边都___________的多边形叫做正多边形.
四、多边形内角和定理:
边形内角和等于___________.正多边形的每个内角的度数为.
五、多边形的外角和定理:
1.多边形的外角和为___________.
外角和定理的应用:①已知外角的度数求正多边形的边数;
②已知正多边形的边数求外角的度数.
一、1.封闭图形2.内角,外角,对角线 二、1.线段 三、1.同一侧2.相等
四、 五、
重点梳理
【重点01】多边形及其相关概念
(1)多边形:在平面内,由一些线段首位顺次相接组成的封闭图形叫做多边形.
(2)正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
【重点02】多边形的内角和
(1)多边形内角和定理:
边形内角和等于.
(2)多边形内角和定理的推理过程:
①从边形的一个顶点出发,可以引出条对角线,这条对角线把边形分成个三角形,又每个三角形的内角和是,所以边形的内角和是.
②在边形内任取一点,连接,,…,,把边形分成个三角形,这个三角形的内角和为,再减去中间的一个周角,即得边形的内角和为.
(3)多边形的内角和的应用:
①己知多边形的边数,求内角和.
②已知多边形的内角和,求边数.
③求正边形的每个内角的度数.
【重点03】多边形的外角和
(1)多边形的外角和定理:多边形的外角和为.
(2)多边形的外角和定理的推理过程:
多边形的每个内角同与它相邻的外角都是邻补角,所以边形的内角和加上外角和为,外角和等于.
(3)多边形的外角和定理的应用:
①已知正多边形的外角度数,求边数.
②已知正多边形的边数,求外角度数.
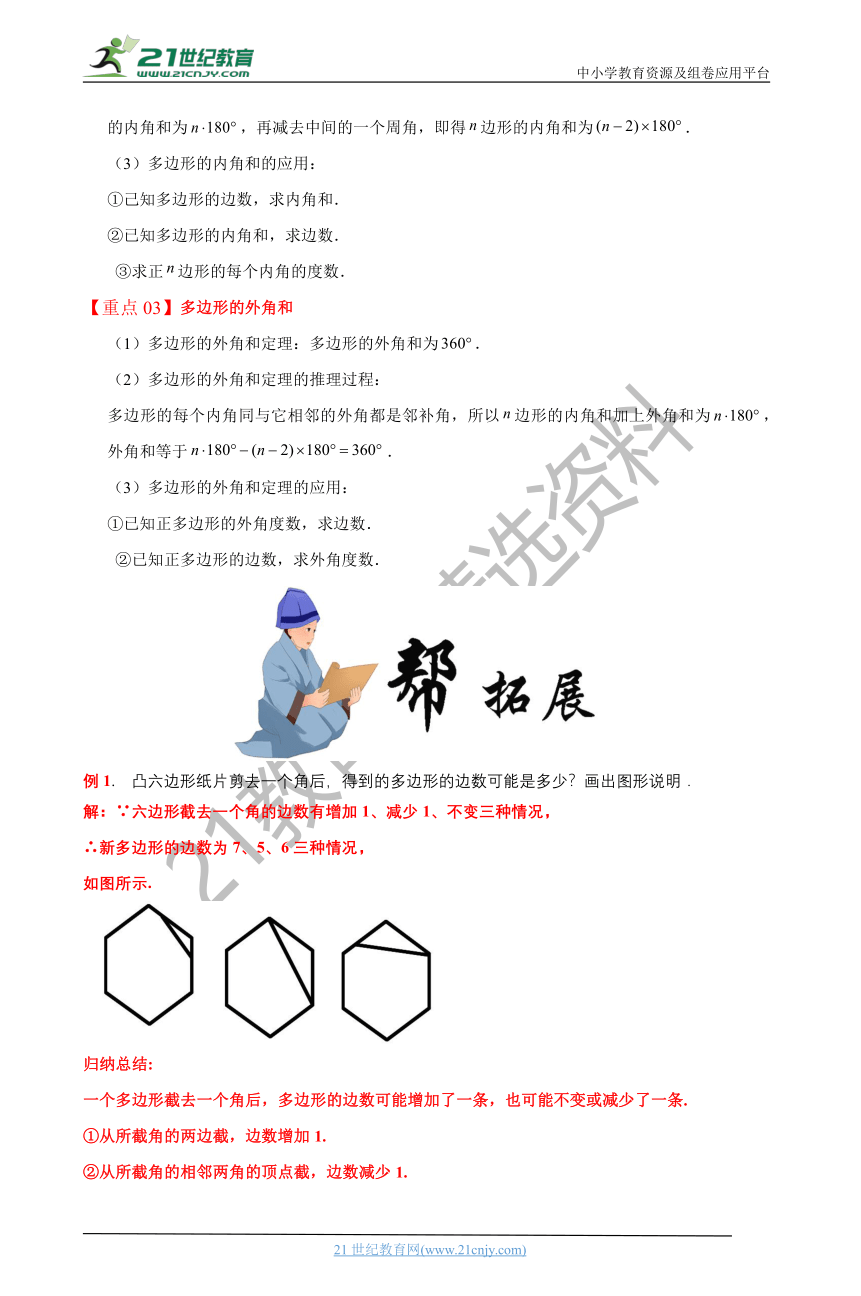
例1. 凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,
∴新多边形的边数为7、5、6三种情况,
如图所示.
归纳总结:
一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条.
①从所截角的两边截,边数增加1.
②从所截角的相邻两角的顶点截,边数减少1.
③从所截角的一边及相邻角的顶点截,边数不变.
例2 过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为21,求这个多边形的边数.21cnjy.com
解:设这个多边形为n边形,则有(n-3)条对角线,所分得的三角形个数为n-2,
∴n-3+n-2=21,
解得n=13.
答:该多边形的边数有13条.
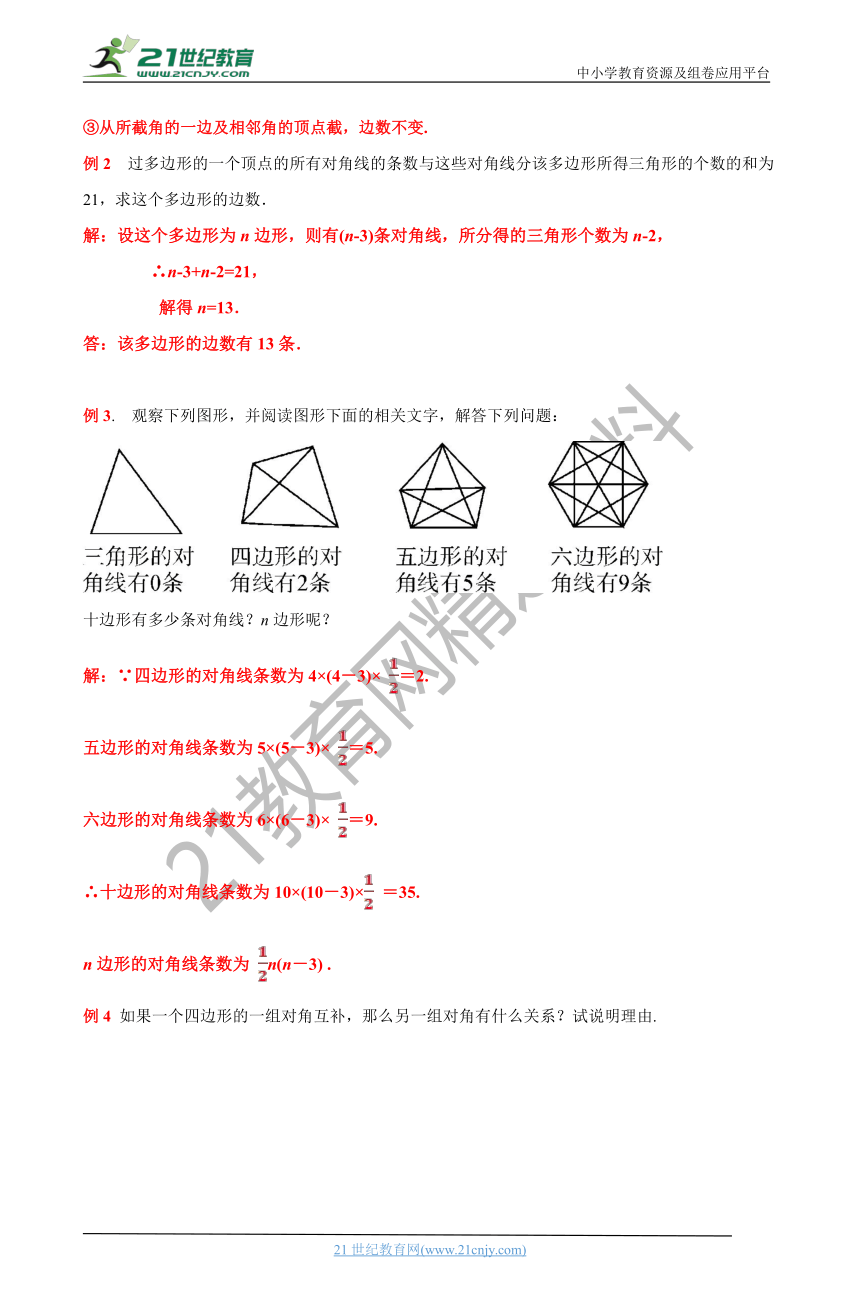
例3. 观察下列图形,并阅读图形下面的相关文字,解答下列问题:
十边形有多少条对角线?n边形呢?
解:∵四边形的对角线条数为4×(4-3)× =2.
五边形的对角线条数为5×(5-3)× =5.
六边形的对角线条数为6×(6-3)× =9.
∴十边形的对角线条数为10×(10-3)× =35.
n边形的对角线条数为 n(n-3) .
例4 如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:如图,四边形ABCD中,∠A+ ∠C =180°.
因为∠A+∠B+∠C+∠D=(4–2) ×180 °= 360 °,
所以∠B+∠D= 360°–(∠A+∠C) = 360°– 180° =180°.
归纳总结:
如果一个四边形的一组对角互补,那么另一组对角也互补.
例5 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?21·世纪*教育网
解:设这个多边形边数为n,则
(n–2)?180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
(8–2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
归纳总结:
多边形的内角和公式 :n边形内角和等于(n–2)×180 °.
①n边形的内角和随边数的增加而增加,每增加一条边其内角和增加180°.
②多边形的内角和是180°的整倍数.
例6 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n–2)?180°,
多边形外角和等于360°,
∴ (n–2)?180°=2× 360?.
解得 n=6.
∴这个多边形的边数为6.
1.如果一个多边形的内角和是它的外角和的n倍,则这个多边形的边数是( )
A.n B.2n-2 C.2n D.2n+2
2.多边形的内角和不可能为( )
A.180° B.680° C.1080° D.1980°
3.下列说法正确的有( )
①由一些线段首位_é?????????????????_的封闭图形叫做多边形;②多边形的两边所在直线组成的角是这个多边形的内角或外角;③各条边都相等的多边形是正多边形.( )www-2-1-cnjy-com
A.0个 B.1个 C.2个 D.3个
4.一个多边形的边数每增加一条,这个多边形的( )
A.内角和增加180° B.外角和增加360°
C.对角线增加一条 D.内角和增加360°
5.如图,足球图片正中的黑色正五边形的内角和是( )
A.180° B.360° C.540° D.720°
6.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是__________.
7. 如图所示_???è????????è?????_ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB=__________度.21教育网
8.如图,正五边形ABCDE中,对角线AC与BE相交于点F,则∠AFE=__________度.
9.如图,该硬币边缘镌刻的正九边形每个内角的度数是__________.
10.如图,六边形ABCDEF的内角都相等,AD∥BC,则∠DAB=__________.
11.若一个多边形的内角和等于它的外角和,则这个多边形的边数为__________.
12.若一个多边形的内角和是540°,则该多边形的边数是__________.
13.八边形的内角和为__________.
14.若正多边形的一个外角是60°,则这个正多边形的内角和是__________.
15.用一条宽度相等的足够长的_??????????????????_(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中,∠BAC=__________度.2-1-c-n-j-y
16. 如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.21*cnjy*com
17. 一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.
18. 如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
1.【答案】D
【解析】设多边形边数为x,则(x-2)·180°=n·360°,即x=2n+2,故选D.
2.【答案】B
【解析】A.∵180?÷180?=1,故A是多边形的内角和;
B.∵680°÷180?=2……14,故B不是多边形的内角和;
C.∵1080?÷180?=6,故C是多边形的内角和;
D.∵1980?÷180?=11,故D是多边形的内角和,故选B.
3.【答案】 A
【解析】①中缺少“在平面内”这一_????????????é??è??_;②中多边形的两边所在直线组成的角中有一个角是多边形内角的对顶角,它既不是多边形的内角,也不是多边形的外角,故错误;③中缺少“各个角都相等”这一条件,故错误.故选A.21世纪教育网版权所有
4.【答案】A
【解析】因为n边形的内角和是(n–2)?180°,外角和为360°,对角线的条数为,当边数增加一条就变成n+1,则内角和是(n–1)?180°,内角和增加:(n–1)?180°–(n–2)?180°=180°;根据多边形的外角和特征,边数变化外角和不变;对角线的条数为 .所以只有A正确,故选A.21·cn·jy·com
5.【答案】C
【解析】黑色正五边形的内角和为:(5-2)×180°=540°,故选C.
6.【答案】5
【解析】∵多边形的内角和与外角和的总和为900°,多边形的外角和是360°,
∴多边形的内角和是900-360=540°,∴多边形的边数是:540°÷180°+2=3+2=5.故答案为:5.
7.【答案】66
【解析】∵五边形ABCDE为正五边形,∴∠EAB=108°,
∵AP是∠EAB的角平分线,∴∠PAB=54°,
∵∠ABP=60°,∴∠APB=180°-60°-54°=66°.故答案为:66.
8.【答案】72
【解析】∵五边形ABCDE是正五边形,∴∠EAB=∠ABC=,
∵BA=BC,∴∠BAC=∠BCA=36°,
同理∠ABE=36°,∴∠AFE=∠ABF+∠BAF=36°+36°=72°.故答案为:72.
9.【答案】140°
【解析】该正九边形内角和=180°×(9-2)=1260°,
则每个内角的度数=140°.故答案为:140°.
10.【答案】60°
【解析】在六边形ABCDEF中,(6-2)×180°=720°,=120°,∴∠B=120°,
∵AD∥BC,∴∠DAB=180°-∠B=60°,故答案为:60°.
11.【答案】4
【解析】设多边形的边数为n,则(n-2)×180°=360°,解得:n=4,故答案为:4.
12.【答案】5
【解析】设这个多边形的边数是n,则(n-2)·180°=540°,解得n=5,故答案为:5.
13.【答案】1080°
【解析】(8-2)·180°=6×180°=1080°.故答案为:1080°.
14.【答案】720°
【解析】该正多边形的边数为:360°÷60°=6,该正多边形的内角和为:(6-2)×180°=720°.
故答案为:720°.
15.【答案】36
【解析】∵∠ABC==108°,△ABC是等腰三角形,
∴∠BAC=∠BCA=36°.故答案为:36°.
16. 【解析】根据五边形的内角_?????????540_°,由∠C,∠D,∠E的度数可求∠EAB+∠ABC的度数,再根据角平分线的定义可得∠PAB与∠PBA的角度和,进一步求得∠P的度数.
解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=540°-∠C-∠D-∠E=230°.
∵AP平分∠EAB,
∴∠PAB= ∠EAB,
同理可得∠ABP= ∠ABC,
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°-∠PAB-∠PBA
=180°? (∠EAB+∠ABC)=180°? ×230°=65°.
17. 【解析】解:设该正多边形的内角是x°,外角是y°,
则得到一个方程组
解得
而任何多边形的外角和是360°,
则该正多边形的边数为360÷120=3,
故这个多边形的每个内角的度数是60°,边数是三条.
18. 【解析】
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠8+∠9+∠5+∠6+∠7
=五边形的内角和=540°.
_21?????????è?????(www.21cnjy.com)_
11.3 多边形及其内角和
目标梳理
学习目标 重点难点
1.了解多边形及其相关概念,理解正多边形及其概念。 2.学会判断一个图形是否是凸多边形
3.理解多边形的对角线的概念
4.能通过不同的方法探索多边形的内角和与外角和公式
5.会应用多边形的内角和与外角和公式进行有关计算
6.通过多边形内角和计算公式的推导,培养学生探索与归纳能力 1.重点:多边形、正多边形的定义及相关概念;多边形的内角和与外角和公式
2.难点:会求多边形的对角线的条数;多边形的内角和公式的推导
知识梳理
一、多边形及其相关概念
1.多边形:在平面内,由一些线段首尾顺次相接组成的___________叫做多边形.多边形按组成它的线段的条数分成三角形、四边形、五边形……,如果一个多边形由条线段组成,那么这个多边形就叫做边形.www.21-cn-jy.com
2.相关概念:①多边形相邻_??¤è???????????è§?_叫做它的___________.②多边形的边与它的邻边的延长线组成的角叫做多边形的___________.③连接多边形不相邻的两个顶点的线段,叫做多边形的___________.【来源:21·世纪·教育·网】
二、多边形的对角线
1.定义:多边形的对角线:连接多边形不相邻的两个顶点的__________,叫做多边形的对角线.
2.规律总结:
①从n边形的一个顶点出发可以引(n-3)条对角线,将n边形分成(n-2)个三角形.
②n边形共有条对角线.
三、凸多边形与正多边形
1.凸多边形:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的___________,那么这个多边形叫做凸多边形.2·1·c·n·j·y
2.正多边形:各个角都相等,各条边都___________的多边形叫做正多边形.
四、多边形内角和定理:
边形内角和等于___________.正多边形的每个内角的度数为.
五、多边形的外角和定理:
1.多边形的外角和为___________.
外角和定理的应用:①已知外角的度数求正多边形的边数;
②已知正多边形的边数求外角的度数.
一、1.封闭图形2.内角,外角,对角线 二、1.线段 三、1.同一侧2.相等
四、 五、
重点梳理
【重点01】多边形及其相关概念
(1)多边形:在平面内,由一些线段首位顺次相接组成的封闭图形叫做多边形.
(2)正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
【重点02】多边形的内角和
(1)多边形内角和定理:
边形内角和等于.
(2)多边形内角和定理的推理过程:
①从边形的一个顶点出发,可以引出条对角线,这条对角线把边形分成个三角形,又每个三角形的内角和是,所以边形的内角和是.
②在边形内任取一点,连接,,…,,把边形分成个三角形,这个三角形的内角和为,再减去中间的一个周角,即得边形的内角和为.
(3)多边形的内角和的应用:
①己知多边形的边数,求内角和.
②已知多边形的内角和,求边数.
③求正边形的每个内角的度数.
【重点03】多边形的外角和
(1)多边形的外角和定理:多边形的外角和为.
(2)多边形的外角和定理的推理过程:
多边形的每个内角同与它相邻的外角都是邻补角,所以边形的内角和加上外角和为,外角和等于.
(3)多边形的外角和定理的应用:
①已知正多边形的外角度数,求边数.
②已知正多边形的边数,求外角度数.
例1. 凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,
∴新多边形的边数为7、5、6三种情况,
如图所示.
归纳总结:
一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条.
①从所截角的两边截,边数增加1.
②从所截角的相邻两角的顶点截,边数减少1.
③从所截角的一边及相邻角的顶点截,边数不变.
例2 过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为21,求这个多边形的边数.21cnjy.com
解:设这个多边形为n边形,则有(n-3)条对角线,所分得的三角形个数为n-2,
∴n-3+n-2=21,
解得n=13.
答:该多边形的边数有13条.
例3. 观察下列图形,并阅读图形下面的相关文字,解答下列问题:
十边形有多少条对角线?n边形呢?
解:∵四边形的对角线条数为4×(4-3)× =2.
五边形的对角线条数为5×(5-3)× =5.
六边形的对角线条数为6×(6-3)× =9.
∴十边形的对角线条数为10×(10-3)× =35.
n边形的对角线条数为 n(n-3) .
例4 如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:如图,四边形ABCD中,∠A+ ∠C =180°.
因为∠A+∠B+∠C+∠D=(4–2) ×180 °= 360 °,
所以∠B+∠D= 360°–(∠A+∠C) = 360°– 180° =180°.
归纳总结:
如果一个四边形的一组对角互补,那么另一组对角也互补.
例5 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?21·世纪*教育网
解:设这个多边形边数为n,则
(n–2)?180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
(8–2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
归纳总结:
多边形的内角和公式 :n边形内角和等于(n–2)×180 °.
①n边形的内角和随边数的增加而增加,每增加一条边其内角和增加180°.
②多边形的内角和是180°的整倍数.
例6 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n–2)?180°,
多边形外角和等于360°,
∴ (n–2)?180°=2× 360?.
解得 n=6.
∴这个多边形的边数为6.
1.如果一个多边形的内角和是它的外角和的n倍,则这个多边形的边数是( )
A.n B.2n-2 C.2n D.2n+2
2.多边形的内角和不可能为( )
A.180° B.680° C.1080° D.1980°
3.下列说法正确的有( )
①由一些线段首位_é?????????????????_的封闭图形叫做多边形;②多边形的两边所在直线组成的角是这个多边形的内角或外角;③各条边都相等的多边形是正多边形.( )www-2-1-cnjy-com
A.0个 B.1个 C.2个 D.3个
4.一个多边形的边数每增加一条,这个多边形的( )
A.内角和增加180° B.外角和增加360°
C.对角线增加一条 D.内角和增加360°
5.如图,足球图片正中的黑色正五边形的内角和是( )
A.180° B.360° C.540° D.720°
6.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是__________.
7. 如图所示_???è????????è?????_ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB=__________度.21教育网
8.如图,正五边形ABCDE中,对角线AC与BE相交于点F,则∠AFE=__________度.
9.如图,该硬币边缘镌刻的正九边形每个内角的度数是__________.
10.如图,六边形ABCDEF的内角都相等,AD∥BC,则∠DAB=__________.
11.若一个多边形的内角和等于它的外角和,则这个多边形的边数为__________.
12.若一个多边形的内角和是540°,则该多边形的边数是__________.
13.八边形的内角和为__________.
14.若正多边形的一个外角是60°,则这个正多边形的内角和是__________.
15.用一条宽度相等的足够长的_??????????????????_(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中,∠BAC=__________度.2-1-c-n-j-y
16. 如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.21*cnjy*com
17. 一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.
18. 如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
1.【答案】D
【解析】设多边形边数为x,则(x-2)·180°=n·360°,即x=2n+2,故选D.
2.【答案】B
【解析】A.∵180?÷180?=1,故A是多边形的内角和;
B.∵680°÷180?=2……14,故B不是多边形的内角和;
C.∵1080?÷180?=6,故C是多边形的内角和;
D.∵1980?÷180?=11,故D是多边形的内角和,故选B.
3.【答案】 A
【解析】①中缺少“在平面内”这一_????????????é??è??_;②中多边形的两边所在直线组成的角中有一个角是多边形内角的对顶角,它既不是多边形的内角,也不是多边形的外角,故错误;③中缺少“各个角都相等”这一条件,故错误.故选A.21世纪教育网版权所有
4.【答案】A
【解析】因为n边形的内角和是(n–2)?180°,外角和为360°,对角线的条数为,当边数增加一条就变成n+1,则内角和是(n–1)?180°,内角和增加:(n–1)?180°–(n–2)?180°=180°;根据多边形的外角和特征,边数变化外角和不变;对角线的条数为 .所以只有A正确,故选A.21·cn·jy·com
5.【答案】C
【解析】黑色正五边形的内角和为:(5-2)×180°=540°,故选C.
6.【答案】5
【解析】∵多边形的内角和与外角和的总和为900°,多边形的外角和是360°,
∴多边形的内角和是900-360=540°,∴多边形的边数是:540°÷180°+2=3+2=5.故答案为:5.
7.【答案】66
【解析】∵五边形ABCDE为正五边形,∴∠EAB=108°,
∵AP是∠EAB的角平分线,∴∠PAB=54°,
∵∠ABP=60°,∴∠APB=180°-60°-54°=66°.故答案为:66.
8.【答案】72
【解析】∵五边形ABCDE是正五边形,∴∠EAB=∠ABC=,
∵BA=BC,∴∠BAC=∠BCA=36°,
同理∠ABE=36°,∴∠AFE=∠ABF+∠BAF=36°+36°=72°.故答案为:72.
9.【答案】140°
【解析】该正九边形内角和=180°×(9-2)=1260°,
则每个内角的度数=140°.故答案为:140°.
10.【答案】60°
【解析】在六边形ABCDEF中,(6-2)×180°=720°,=120°,∴∠B=120°,
∵AD∥BC,∴∠DAB=180°-∠B=60°,故答案为:60°.
11.【答案】4
【解析】设多边形的边数为n,则(n-2)×180°=360°,解得:n=4,故答案为:4.
12.【答案】5
【解析】设这个多边形的边数是n,则(n-2)·180°=540°,解得n=5,故答案为:5.
13.【答案】1080°
【解析】(8-2)·180°=6×180°=1080°.故答案为:1080°.
14.【答案】720°
【解析】该正多边形的边数为:360°÷60°=6,该正多边形的内角和为:(6-2)×180°=720°.
故答案为:720°.
15.【答案】36
【解析】∵∠ABC==108°,△ABC是等腰三角形,
∴∠BAC=∠BCA=36°.故答案为:36°.
16. 【解析】根据五边形的内角_?????????540_°,由∠C,∠D,∠E的度数可求∠EAB+∠ABC的度数,再根据角平分线的定义可得∠PAB与∠PBA的角度和,进一步求得∠P的度数.
解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=540°-∠C-∠D-∠E=230°.
∵AP平分∠EAB,
∴∠PAB= ∠EAB,
同理可得∠ABP= ∠ABC,
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°-∠PAB-∠PBA
=180°? (∠EAB+∠ABC)=180°? ×230°=65°.
17. 【解析】解:设该正多边形的内角是x°,外角是y°,
则得到一个方程组
解得
而任何多边形的外角和是360°,
则该正多边形的边数为360÷120=3,
故这个多边形的每个内角的度数是60°,边数是三条.
18. 【解析】
解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠8+∠9+∠5+∠6+∠7
=五边形的内角和=540°.
_21?????????è?????(www.21cnjy.com)_
