12.2 三角形全等的判定-2020-2021数学八上同步课堂帮帮帮(含解析)
文档属性
| 名称 | 12.2 三角形全等的判定-2020-2021数学八上同步课堂帮帮帮(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
12.2 三角形全等的判定
目标梳理
学习目标 重点难点
1.了解三角形全等的“边边边”的条件 2.掌握三角形全等的“边角边”的条件
3.探索三角形全等的“角边角”和“角角边”的条件
4.掌握直角三角形全等的条件,并能运用其解决一些实际问题
5.会用三角形判定定理证明两个三角形全等并能应用其解决实际问题 1.重点:三角形全等条件的探索过程;
2.难点:寻找判定三角形全等的条件;
知识梳理
一、判定两个三角形全等的基本事实:边边边(SSS)
1.基本事实:三边分别相等的两个三角形全等,简写成“__________”或“SSS”.
2.这个基本事实告诉我们:当三角形的三边确定后,其形状、大小也随之确定.这也是三角形具有稳定性的原因.21教育网
二、判定两个三角形全等的基本事实:边角边(SAS)
1.基本事实:两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“__________”.
2.此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.21cnjy.com
【注意】1.此方法是证明两个三角_?????¨???????????¨_的方法之一,应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要误认为有两边一角就能判定两个三角形全等.21·cn·jy·com
2.在书写时也要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.www.21-cn-jy.com
三、判定两个三角形全等的基本事实:角边角(ASA)
1.基本事实:两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“__________”.21·世纪*教育网
2.用“ASA”来判定两个三角形全等,一定要证明这两个三角形有两个角以及这两个角的夹边分别相等,证明时要加强对夹边的认识.www-2-1-cnjy-com
四、判定两个三角形全等的基本事实:角角边(AAS)
1.基本事实:两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“__________”.2-1-c-n-j-y
2.这一结论很容易由“ASA”推得,将这一结论与“ASA”结合起来,即可得出:两个三角形如果具备两角和一条边对应相等,就可判定其全等.【来源:21cnj*y.co*m】
五、直角三角形全等的判定方法:斜边、直角边(HL)
1.基本事实:斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“________”.【来源:21·世纪·教育·网】
2.“HL”定理是直角三角形所独有的,对于一般三角形不成立.
【归纳】判定两个三角形全等常用的思路方法如下:
一、1.边边边 二、1.SAS 三、1.ASA 四、1.AAS 五、1.HL
重点梳理
【重点01】用边边边(SSS)证明三角形全等
明确要证明全等的两个三角形,在书写两个三角形全等时,“≌”左边三角形的三边与“≌”右边三角形的三边的前后顺序要保持一致.【版权所有:21教育】
【重点02】用边角边(SAS)证明三角形全等
此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.21教育名师原创作品
【重点03】用角边角、角角边(ASA、AAS)证明三角形全等
(1)不能说“有两_è§???????è????????_相等的两个三角形全等”,这是因为:假设这条边是两角的夹边,则根据角边角可知正确;假设一个三角形的一边是两角的夹边,而与另一个三角形相等的边是其中一等角的对边,则两个三角形不一定全等.
(2)有三个角对应相等的两个三角形不一定全等.
【重点04】用斜边、直角边(HL)证明直角三角形全等
(1)当证明两个直角三角形全等时,若不适合应用“HL”,也可考虑用“SAS”“ASA”或“AAS”来证明.
(2)在用一般方法证明时,因为两_??????è§????è§????_中已具备一对直角相等的条件,故只需找另外两个条件即可,在实际证明中可根据条件灵活选用不同的方法.
【重点05】全等三角形的判定和性质的综合
寻找解决问题的_???è·?????????????_从求证的结论出发,结合已知条件,逐步寻求解决问题所需要的条件.同时要注意对图形本身隐含条件的挖掘,如对顶角、公共角、公共边等.
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A与BC中点D的支架.
求证:(1)△ABD ≌△ACD. (2)∠BAD = ∠CAD.
证明:∵ D 是BC中点,
∴ BD =DC.
在△ABD 与△ACD 中,
AB =AC (已知)
BD =CD (已证)
AD =AD (公共边)
∴ △ABD ≌ △ACD ( SSS ).
(2) 由(1)得△ABD≌△ACD ,
∴ ∠BAD= ∠CAD.
(全等三角形对应角相等)
例2 已知:如图,AB=AC,AD=AE,BD=CE. 求证:∠BAC=∠DAE.
证明:在△ ABD和△ ACE中,
AB=AC,
AD=AE,
BD=CE,
∴ △ ABD≌ △ ACE(SSS),
∴∠BAD=∠CAE.
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
例3 如果AB=CB ,∠ ABD= ∠ CBD,那么 △ ABD 和△ CBD 全等吗?
证明:在△ABD 和△ CBD中,
AB=CB(已知),
∠ABD= ∠CBD(已知),
BD=BD(公共边),
∴ △ ABD≌△CBD ( SAS).
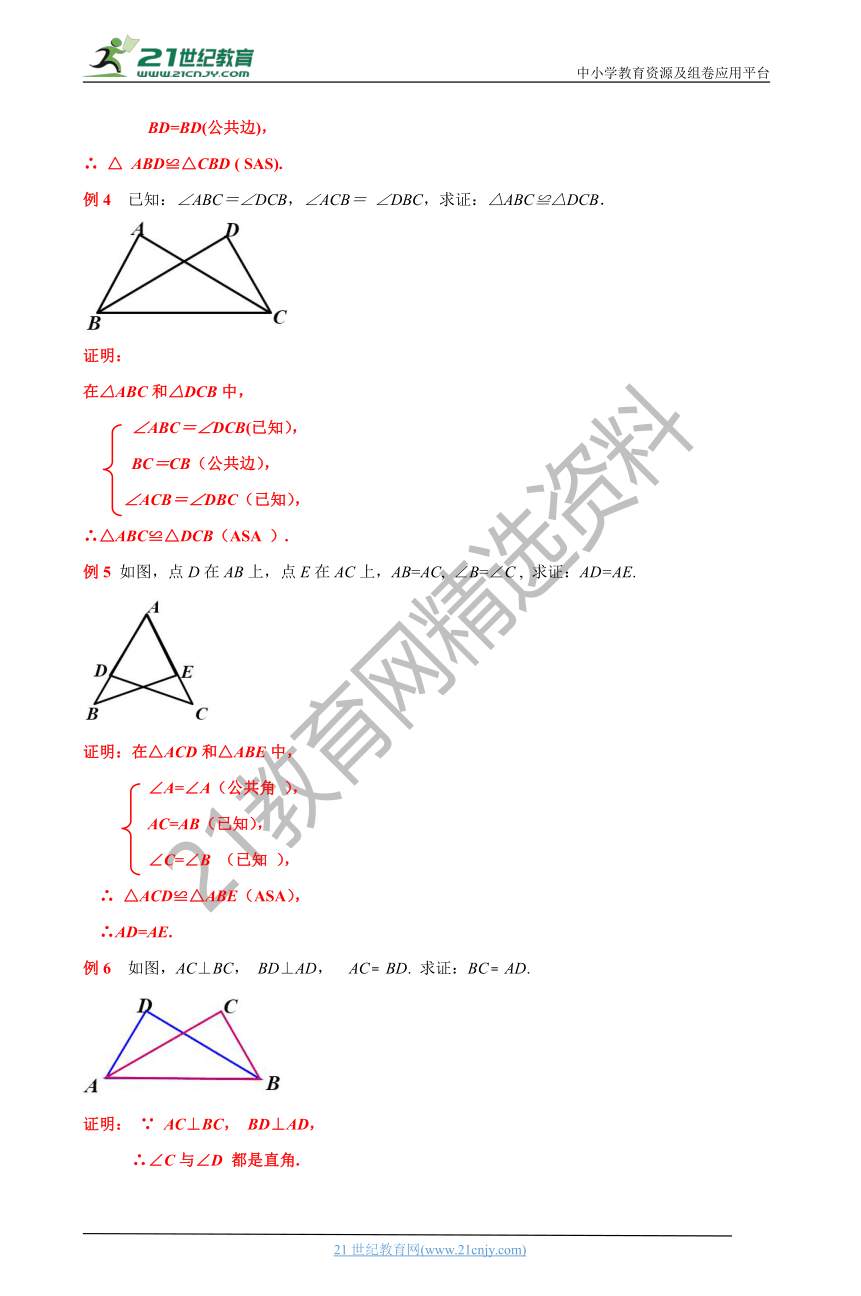
例4 已知:∠ABC=∠DCB,∠ACB= ∠DBC,求证:△ABC≌△DCB.
证明:
在△ABC和△DCB中,
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
∴△ABC≌△DCB(ASA ).
例5 如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C , 求证:AD=AE.
证明:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
∴ △ACD≌△ABE(ASA),
∴AD=AE.
例6 如图,AC⊥BC, BD⊥AD, AC﹦BD. 求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D 都是直角.
在 Rt△ABC 和Rt△BAD 中,
AB=BA,
AC=BD
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
例7 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.2·1·c·n·j·y
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF. 即BC=BE.
1.如图,若∠ABC=∠DCB,当添加下列条件时,仍不能判断△ABC≌△DCB的是( )
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
2.如图,点在的边上,用尺规作出了,作图痕迹中,是( )
A.以点为圆心,为半径的弧 B.以点为圆心,为半径的弧
C.以点为圆心,为半径的弧 D.以点为圆心,为半径的弧
3.下列条件中能作出唯一三角形的是( )
A.AB=4 cm,BC=3 cm,AC=5 cm B.AB=2 cm,BC=6 cm,AC=4 cm【出处:21教育名师】
C.∠A=∠B=∠C=60° D.∠A=30°,∠B=60°,∠C=90°
4.如图,小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中,要使DC=AB,则AO、BO、CO、DO应满足下列的条件是21*cnjy*com
A.AO=CO B.AO=CO且BO=DO
C.AC=BD D.BO=DO
5.如图,D?E?F分别为△ABC边AC?AB?BC上的点,∠A=∠1=∠C,DE=DF.下面的结论一定成立的是( )
A.AE=FC B.AE=DE C.AE+FC=AC D.AD+FC=AB
6.已知两角及其夹边作三角形,所用的基本作图方法是( )
A.平分已知角
B.作已知直线的垂线
C.作一个角等于已知角及作一条线段等于已知线段
D.作已知直线的平行线
7.如图,在四边形中,,,,,则图中的全等三角形有( )
A.2对 B.3对 C.4对 D.5对
8.如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )
A. B. C. D.
9.如图,D为△ABC内一点,且AD=BD,若∠ACD=∠DAB=45°,AC=5,则S△ABC=__________.
10.如图,中,,,点D为AB的中点,点P在线段BC上以的速度由点B向点C移动,同时,点Q在线段CA上由点C向点A移动,若点Q的移动速度与点P的移动速度相同,则经过__________秒后,≌.
11.如图,在△ABC中,AC=3,中线AD=5,则边AB的取值范围是__________.
12.如图,已_?????¨???ABC_和△DEF中,∠B=∠E,BF=CE,点B、F、C、E在同一条直线上,若使△ABC≌△DEF,则还需添加的一个条件是__________(只填一个即可).
13.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是_________.(不添加任何字母和辅助线)
14.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,求证:AF=DE.
15.已知:如图,点B,D在线段AE上,AD=BE,AC∥EF,∠C=∠F.求证:BC=DF.
16.如图,在△ABC中_??????BAC=_90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.
(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
17.已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
18.如图,已知∠C=∠D=90°,BC与AD交于点E,AC=BD,求证:AE=BE.
19.如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
20.如图,AB=DE,BF=EC,∠B=∠E,求证:AC∥DF.
1.【答案】D
【解析】A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
D、添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意.故选D.
2.【答案】D
【解析】根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧.故选D.
3.【答案】A
【解析】A.符合全等三角形的SSS,能作出唯一三角形,故该选项符合题意,
B.AB+AC=BC,不符合三角形三边之间的关系,不能作出三角形;故该选项不符合题意,
C.属于全等三角形判定中的AAA的情况,不能作出唯一三角形;故该选项不符合题意,
D.属于全等三角形判定中的AAA的情况,不能作出唯一三角形;故该选项不符合题意,
故选A.
4.【答案】B
【解析】如图,连接CD.
AO=CO且BO=DO,(对顶角相等),所以,
则DC=AB.故选B.
5.【答案】C
【解析】∵∠A+∠AED+∠ADE=180°,∠ADE+∠1+∠CDF=180°,∠A=∠1,
∴∠AED+∠ADE=∠ADE+∠CDF,∴∠AED=∠CDF,
又∵∠A=∠C,DE=DF,
∴△ADE≌△CFD,∴AE=CD,AD=CF,
又∵AD+CD=AC,∴AE+FC=AC,
∴上述四个结论中,正确的是C中的结论,其余三个结论都是错误的,故选C.
6.【答案】C
【解析】已知两角及其夹边作三_è§????????????????_一条线段等于已知线段,再在线段的两个端点分别作两个角等于已知角,故所用的基本作图方法是作一个角等于已知角及作一条线段等于已知线段.21世纪教育网版权所有
故选C.
7.【答案】C
【解析】在△AOB和△COD中,OA=OC,OB=OD,∠AOB=∠COD,∴△AOB≌△COD,
同理可证△AOD≌△COB,在△ABD和△CDB中,AB=CD,AD=CB,BD=DB,∴△ABD≌△CDB,21*cnjy*com
同理可证△ABC≌△DCA,故选C.
8.【答案】C
【解析】∵∠ADB=∠AEC=100°,∴∠ADE=∠AED=80°,∴AD=AE,
∵∠BAD=50°,∴∠B=180°-100°-50°=30°,
在△ADB与△AEC中,,
∴△ADB≌△AEC(SAS),
∴AB=AC,
∴∠B=∠C=30°,
故选C.
9.【答案】
【解析】如图,过D作FD⊥CD交AC于F,连接BF.
∵∠ACD=45°,∴∠CFD=45°,∴FD=CD.
∵∠CDF=∠ADB=90°,∴∠CDA=∠FDB.
在△ADC和△BDF中,∵CD=DF,∠CDA=∠FDB,AD=DB,
∴△ADC≌△BDF,∴∠ACD=∠BFD=45°,AC=BF.
∵∠CFD=45°,∴∠BFC=90°,∴BF⊥AC,∴S△ABC=AC?BF=×5×5=.故答案为:.
10.【答案】1
【解析】∵AB=AC,∴∠B=∠C,
设点P、Q的运动时间为t,则BP=3t,CQ=3t,
∵AB=10 cm,BC=8 cm,点D为AB的中点,
∴BD=×10=5 cm,PC=(8-3t)cm,
∵△BPD≌△CQP,
∴BD=PC,BP=CQ,
∴5=8-3t且3t=3t,
解得t=1,
故答案为:1.
11.【答案】7【解析】如图,延长AD到E,使得DE=AD=5,连接EC.
∵AD=DE,∠ADB=∠EDC,BD=DC,∴△ADB≌△EDC,
∴EC=AB,∴,即,.
故答案为:.
12.【答案】AB=DE
【解析】添加AB=DE;
∵BF=CE,∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF,
故答案为:AB=DE.
13.【答案】AB=AC或∠ADC=∠AEB或∠ABE=∠ACD
【解析】∵∠A=∠A,AD=AE,
∴可以添加AB=AC,此时满足SAS;
添加条件∠ADC=∠AEB,此时满足ASA;
添加条件∠ABE=∠ACD,此时满足AAS,
故答案为:AB=AC或∠ADC=∠AEB或∠ABE=∠ACD.
14.【解析】∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
在△ABF和△DCE中,,
∴△ABF≌△DCE,
∴AF=DE.
15.【解析】∵AD=BE,
∴AD-BD=BE-BD,
∴AB=ED,
∵AC∥EF,
∴∠A=∠E,
在△ABC和△EDF中,,
∴△ABC≌△EDF,
∴BC=DF.
16.【解析】(1)∵AB=AE,D为线段BE的中点,
∴AD⊥BC,
∴∠C+∠DAC=90°,
∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
∴∠C=∠BAD.
(2)∵AF∥BC,
∴∠FAE=∠AEB,
∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠FAE,且∠AEF=∠BAC=90°,AB=AE,
∴△ABC≌△EAF,
∴AC=EF.
17.【解析】由∠ECB=70°得∠ACB=110°,
又∵∠D=110°,
∴∠ACB=∠D,
∵AB∥DE,
∴∠CAB=∠E,
∴在△ABC和△EAD中,,
∴△ABC≌△EAD.
18.【解析】∵∠C=∠D=90°,
∴△ACB和△BDA是直角三角形,
在Rt△ACB和Rt△BDA中,,
∴Rt△ACB≌Rt△BDA,
∴∠ABC=∠BAD,
∴AE=BE.
19.【解析】(1)∵BE平分∠ABC,
∴∠ABE=∠DBE,
在△ABE和△DBE中,,
∴△ABE≌△DBE.
(2)∵∠A=100°,∠C=50°,
∴∠ABC=30°,
∵BE平分∠ABC,
∴∠ABE=∠DBE∠ABC=15°,
在△ABE中,∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°.
20.【解析】∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF,
∴∠ACB=∠DFE,
∴AC∥DF.
_21?????????è?????(www.21cnjy.com)_
12.2 三角形全等的判定
目标梳理
学习目标 重点难点
1.了解三角形全等的“边边边”的条件 2.掌握三角形全等的“边角边”的条件
3.探索三角形全等的“角边角”和“角角边”的条件
4.掌握直角三角形全等的条件,并能运用其解决一些实际问题
5.会用三角形判定定理证明两个三角形全等并能应用其解决实际问题 1.重点:三角形全等条件的探索过程;
2.难点:寻找判定三角形全等的条件;
知识梳理
一、判定两个三角形全等的基本事实:边边边(SSS)
1.基本事实:三边分别相等的两个三角形全等,简写成“__________”或“SSS”.
2.这个基本事实告诉我们:当三角形的三边确定后,其形状、大小也随之确定.这也是三角形具有稳定性的原因.21教育网
二、判定两个三角形全等的基本事实:边角边(SAS)
1.基本事实:两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“__________”.
2.此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.21cnjy.com
【注意】1.此方法是证明两个三角_?????¨???????????¨_的方法之一,应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要误认为有两边一角就能判定两个三角形全等.21·cn·jy·com
2.在书写时也要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.www.21-cn-jy.com
三、判定两个三角形全等的基本事实:角边角(ASA)
1.基本事实:两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“__________”.21·世纪*教育网
2.用“ASA”来判定两个三角形全等,一定要证明这两个三角形有两个角以及这两个角的夹边分别相等,证明时要加强对夹边的认识.www-2-1-cnjy-com
四、判定两个三角形全等的基本事实:角角边(AAS)
1.基本事实:两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“__________”.2-1-c-n-j-y
2.这一结论很容易由“ASA”推得,将这一结论与“ASA”结合起来,即可得出:两个三角形如果具备两角和一条边对应相等,就可判定其全等.【来源:21cnj*y.co*m】
五、直角三角形全等的判定方法:斜边、直角边(HL)
1.基本事实:斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“________”.【来源:21·世纪·教育·网】
2.“HL”定理是直角三角形所独有的,对于一般三角形不成立.
【归纳】判定两个三角形全等常用的思路方法如下:
一、1.边边边 二、1.SAS 三、1.ASA 四、1.AAS 五、1.HL
重点梳理
【重点01】用边边边(SSS)证明三角形全等
明确要证明全等的两个三角形,在书写两个三角形全等时,“≌”左边三角形的三边与“≌”右边三角形的三边的前后顺序要保持一致.【版权所有:21教育】
【重点02】用边角边(SAS)证明三角形全等
此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.21教育名师原创作品
【重点03】用角边角、角角边(ASA、AAS)证明三角形全等
(1)不能说“有两_è§???????è????????_相等的两个三角形全等”,这是因为:假设这条边是两角的夹边,则根据角边角可知正确;假设一个三角形的一边是两角的夹边,而与另一个三角形相等的边是其中一等角的对边,则两个三角形不一定全等.
(2)有三个角对应相等的两个三角形不一定全等.
【重点04】用斜边、直角边(HL)证明直角三角形全等
(1)当证明两个直角三角形全等时,若不适合应用“HL”,也可考虑用“SAS”“ASA”或“AAS”来证明.
(2)在用一般方法证明时,因为两_??????è§????è§????_中已具备一对直角相等的条件,故只需找另外两个条件即可,在实际证明中可根据条件灵活选用不同的方法.
【重点05】全等三角形的判定和性质的综合
寻找解决问题的_???è·?????????????_从求证的结论出发,结合已知条件,逐步寻求解决问题所需要的条件.同时要注意对图形本身隐含条件的挖掘,如对顶角、公共角、公共边等.
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A与BC中点D的支架.
求证:(1)△ABD ≌△ACD. (2)∠BAD = ∠CAD.
证明:∵ D 是BC中点,
∴ BD =DC.
在△ABD 与△ACD 中,
AB =AC (已知)
BD =CD (已证)
AD =AD (公共边)
∴ △ABD ≌ △ACD ( SSS ).
(2) 由(1)得△ABD≌△ACD ,
∴ ∠BAD= ∠CAD.
(全等三角形对应角相等)
例2 已知:如图,AB=AC,AD=AE,BD=CE. 求证:∠BAC=∠DAE.
证明:在△ ABD和△ ACE中,
AB=AC,
AD=AE,
BD=CE,
∴ △ ABD≌ △ ACE(SSS),
∴∠BAD=∠CAE.
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
例3 如果AB=CB ,∠ ABD= ∠ CBD,那么 △ ABD 和△ CBD 全等吗?
证明:在△ABD 和△ CBD中,
AB=CB(已知),
∠ABD= ∠CBD(已知),
BD=BD(公共边),
∴ △ ABD≌△CBD ( SAS).
例4 已知:∠ABC=∠DCB,∠ACB= ∠DBC,求证:△ABC≌△DCB.
证明:
在△ABC和△DCB中,
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
∴△ABC≌△DCB(ASA ).
例5 如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C , 求证:AD=AE.
证明:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
∴ △ACD≌△ABE(ASA),
∴AD=AE.
例6 如图,AC⊥BC, BD⊥AD, AC﹦BD. 求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D 都是直角.
在 Rt△ABC 和Rt△BAD 中,
AB=BA,
AC=BD
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
例7 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.2·1·c·n·j·y
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF. 即BC=BE.
1.如图,若∠ABC=∠DCB,当添加下列条件时,仍不能判断△ABC≌△DCB的是( )
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
2.如图,点在的边上,用尺规作出了,作图痕迹中,是( )
A.以点为圆心,为半径的弧 B.以点为圆心,为半径的弧
C.以点为圆心,为半径的弧 D.以点为圆心,为半径的弧
3.下列条件中能作出唯一三角形的是( )
A.AB=4 cm,BC=3 cm,AC=5 cm B.AB=2 cm,BC=6 cm,AC=4 cm【出处:21教育名师】
C.∠A=∠B=∠C=60° D.∠A=30°,∠B=60°,∠C=90°
4.如图,小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中,要使DC=AB,则AO、BO、CO、DO应满足下列的条件是21*cnjy*com
A.AO=CO B.AO=CO且BO=DO
C.AC=BD D.BO=DO
5.如图,D?E?F分别为△ABC边AC?AB?BC上的点,∠A=∠1=∠C,DE=DF.下面的结论一定成立的是( )
A.AE=FC B.AE=DE C.AE+FC=AC D.AD+FC=AB
6.已知两角及其夹边作三角形,所用的基本作图方法是( )
A.平分已知角
B.作已知直线的垂线
C.作一个角等于已知角及作一条线段等于已知线段
D.作已知直线的平行线
7.如图,在四边形中,,,,,则图中的全等三角形有( )
A.2对 B.3对 C.4对 D.5对
8.如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )
A. B. C. D.
9.如图,D为△ABC内一点,且AD=BD,若∠ACD=∠DAB=45°,AC=5,则S△ABC=__________.
10.如图,中,,,点D为AB的中点,点P在线段BC上以的速度由点B向点C移动,同时,点Q在线段CA上由点C向点A移动,若点Q的移动速度与点P的移动速度相同,则经过__________秒后,≌.
11.如图,在△ABC中,AC=3,中线AD=5,则边AB的取值范围是__________.
12.如图,已_?????¨???ABC_和△DEF中,∠B=∠E,BF=CE,点B、F、C、E在同一条直线上,若使△ABC≌△DEF,则还需添加的一个条件是__________(只填一个即可).
13.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是_________.(不添加任何字母和辅助线)
14.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,求证:AF=DE.
15.已知:如图,点B,D在线段AE上,AD=BE,AC∥EF,∠C=∠F.求证:BC=DF.
16.如图,在△ABC中_??????BAC=_90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.
(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
17.已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
18.如图,已知∠C=∠D=90°,BC与AD交于点E,AC=BD,求证:AE=BE.
19.如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
20.如图,AB=DE,BF=EC,∠B=∠E,求证:AC∥DF.
1.【答案】D
【解析】A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
D、添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意.故选D.
2.【答案】D
【解析】根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧.故选D.
3.【答案】A
【解析】A.符合全等三角形的SSS,能作出唯一三角形,故该选项符合题意,
B.AB+AC=BC,不符合三角形三边之间的关系,不能作出三角形;故该选项不符合题意,
C.属于全等三角形判定中的AAA的情况,不能作出唯一三角形;故该选项不符合题意,
D.属于全等三角形判定中的AAA的情况,不能作出唯一三角形;故该选项不符合题意,
故选A.
4.【答案】B
【解析】如图,连接CD.
AO=CO且BO=DO,(对顶角相等),所以,
则DC=AB.故选B.
5.【答案】C
【解析】∵∠A+∠AED+∠ADE=180°,∠ADE+∠1+∠CDF=180°,∠A=∠1,
∴∠AED+∠ADE=∠ADE+∠CDF,∴∠AED=∠CDF,
又∵∠A=∠C,DE=DF,
∴△ADE≌△CFD,∴AE=CD,AD=CF,
又∵AD+CD=AC,∴AE+FC=AC,
∴上述四个结论中,正确的是C中的结论,其余三个结论都是错误的,故选C.
6.【答案】C
【解析】已知两角及其夹边作三_è§????????????????_一条线段等于已知线段,再在线段的两个端点分别作两个角等于已知角,故所用的基本作图方法是作一个角等于已知角及作一条线段等于已知线段.21世纪教育网版权所有
故选C.
7.【答案】C
【解析】在△AOB和△COD中,OA=OC,OB=OD,∠AOB=∠COD,∴△AOB≌△COD,
同理可证△AOD≌△COB,在△ABD和△CDB中,AB=CD,AD=CB,BD=DB,∴△ABD≌△CDB,21*cnjy*com
同理可证△ABC≌△DCA,故选C.
8.【答案】C
【解析】∵∠ADB=∠AEC=100°,∴∠ADE=∠AED=80°,∴AD=AE,
∵∠BAD=50°,∴∠B=180°-100°-50°=30°,
在△ADB与△AEC中,,
∴△ADB≌△AEC(SAS),
∴AB=AC,
∴∠B=∠C=30°,
故选C.
9.【答案】
【解析】如图,过D作FD⊥CD交AC于F,连接BF.
∵∠ACD=45°,∴∠CFD=45°,∴FD=CD.
∵∠CDF=∠ADB=90°,∴∠CDA=∠FDB.
在△ADC和△BDF中,∵CD=DF,∠CDA=∠FDB,AD=DB,
∴△ADC≌△BDF,∴∠ACD=∠BFD=45°,AC=BF.
∵∠CFD=45°,∴∠BFC=90°,∴BF⊥AC,∴S△ABC=AC?BF=×5×5=.故答案为:.
10.【答案】1
【解析】∵AB=AC,∴∠B=∠C,
设点P、Q的运动时间为t,则BP=3t,CQ=3t,
∵AB=10 cm,BC=8 cm,点D为AB的中点,
∴BD=×10=5 cm,PC=(8-3t)cm,
∵△BPD≌△CQP,
∴BD=PC,BP=CQ,
∴5=8-3t且3t=3t,
解得t=1,
故答案为:1.
11.【答案】7
∵AD=DE,∠ADB=∠EDC,BD=DC,∴△ADB≌△EDC,
∴EC=AB,∴,即,.
故答案为:.
12.【答案】AB=DE
【解析】添加AB=DE;
∵BF=CE,∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF,
故答案为:AB=DE.
13.【答案】AB=AC或∠ADC=∠AEB或∠ABE=∠ACD
【解析】∵∠A=∠A,AD=AE,
∴可以添加AB=AC,此时满足SAS;
添加条件∠ADC=∠AEB,此时满足ASA;
添加条件∠ABE=∠ACD,此时满足AAS,
故答案为:AB=AC或∠ADC=∠AEB或∠ABE=∠ACD.
14.【解析】∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
在△ABF和△DCE中,,
∴△ABF≌△DCE,
∴AF=DE.
15.【解析】∵AD=BE,
∴AD-BD=BE-BD,
∴AB=ED,
∵AC∥EF,
∴∠A=∠E,
在△ABC和△EDF中,,
∴△ABC≌△EDF,
∴BC=DF.
16.【解析】(1)∵AB=AE,D为线段BE的中点,
∴AD⊥BC,
∴∠C+∠DAC=90°,
∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
∴∠C=∠BAD.
(2)∵AF∥BC,
∴∠FAE=∠AEB,
∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠FAE,且∠AEF=∠BAC=90°,AB=AE,
∴△ABC≌△EAF,
∴AC=EF.
17.【解析】由∠ECB=70°得∠ACB=110°,
又∵∠D=110°,
∴∠ACB=∠D,
∵AB∥DE,
∴∠CAB=∠E,
∴在△ABC和△EAD中,,
∴△ABC≌△EAD.
18.【解析】∵∠C=∠D=90°,
∴△ACB和△BDA是直角三角形,
在Rt△ACB和Rt△BDA中,,
∴Rt△ACB≌Rt△BDA,
∴∠ABC=∠BAD,
∴AE=BE.
19.【解析】(1)∵BE平分∠ABC,
∴∠ABE=∠DBE,
在△ABE和△DBE中,,
∴△ABE≌△DBE.
(2)∵∠A=100°,∠C=50°,
∴∠ABC=30°,
∵BE平分∠ABC,
∴∠ABE=∠DBE∠ABC=15°,
在△ABE中,∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°.
20.【解析】∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF,
∴∠ACB=∠DFE,
∴AC∥DF.
_21?????????è?????(www.21cnjy.com)_
