人教版八年级数学上册 11.2 与三角形有关的角 同步培优训练(word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 11.2 与三角形有关的角 同步培优训练(word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 280.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览

文档简介
人教版 八年级数学上册 11.2 与三角形有关的角 同步培优训练
一、选择题
1. 已知在△ABC中,∠A=70°,∠B=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
2. 在△ABC中,∠A,∠C与∠B处的外角的度数如图所示,则x的值是( )
A.80 B.70 C.65 D.60
3. 在Rt△ABC中,∠C=90°,∠A-∠B=50°,则∠A的度数为( )
A.80° B.70° C.60° D.50°
4. 如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A.65° B.70° C.75° D.85°
5. 一个三角形三个内角的度数之比为2∶3∶4,这个三角形是( )
A. 直角三角形 B. 等腰三角形
C. 锐角三角形 D. 钝角三角形
6. 若三角形的三个内角的度数之比为2∶3∶7,则这个三角形的最大内角是( )
A.75° B.90° C.105° D.120°
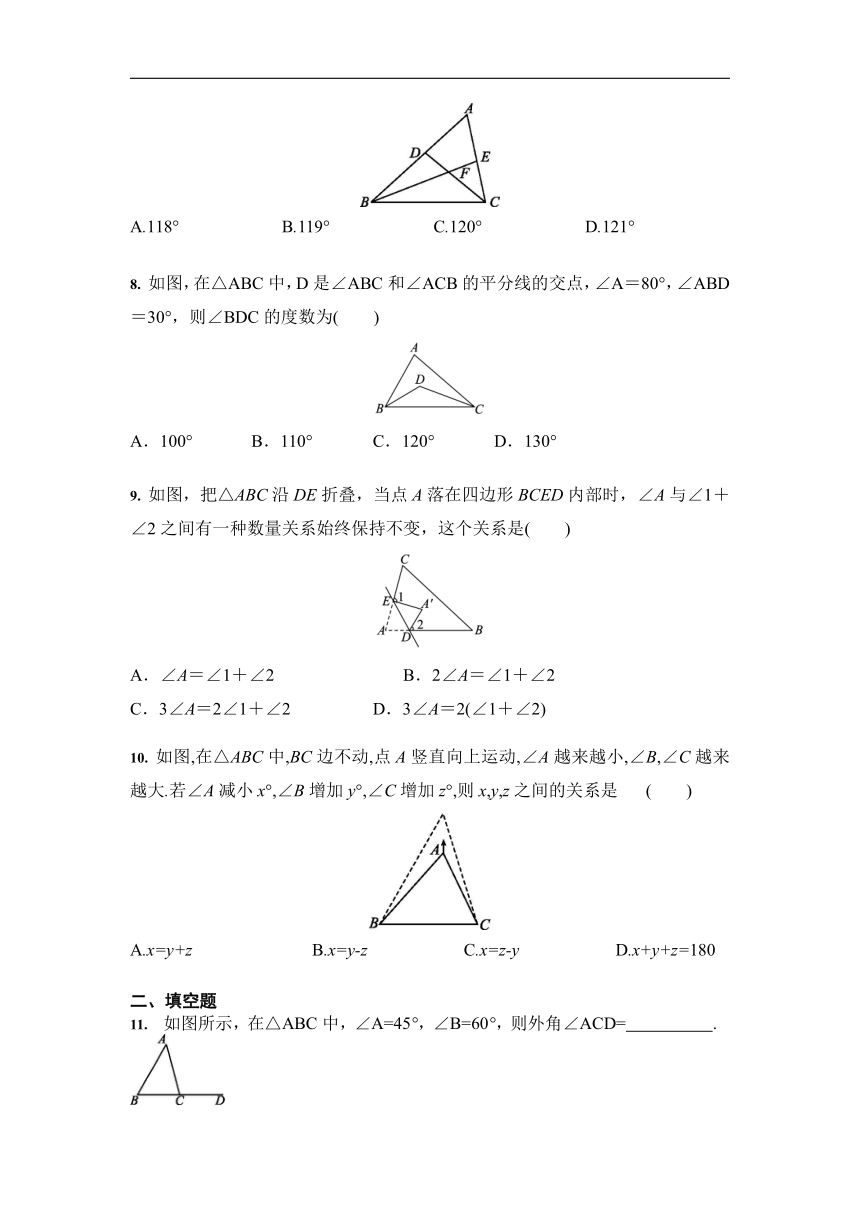
7. 如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为 ( )
A.118° B.119° C.120° D.121°
8. 如图,在△ABC中,D是∠ABC和∠ACB的平分线的交点,∠A=80°,∠ABD=30°,则∠BDC的度数为( )
A.100° B.110° C.120° D.130°
9. 如图,把△ABC沿DE折叠,当点A落在四边形BCED内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,这个关系是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
10. 如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是 ( )
A.x=y+z B.x=y-z C.x=z-y D.x+y+z=180
二、填空题
11. 如图所示,在△ABC中,∠A=45°,∠B=60°,则外角∠ACD= . ?
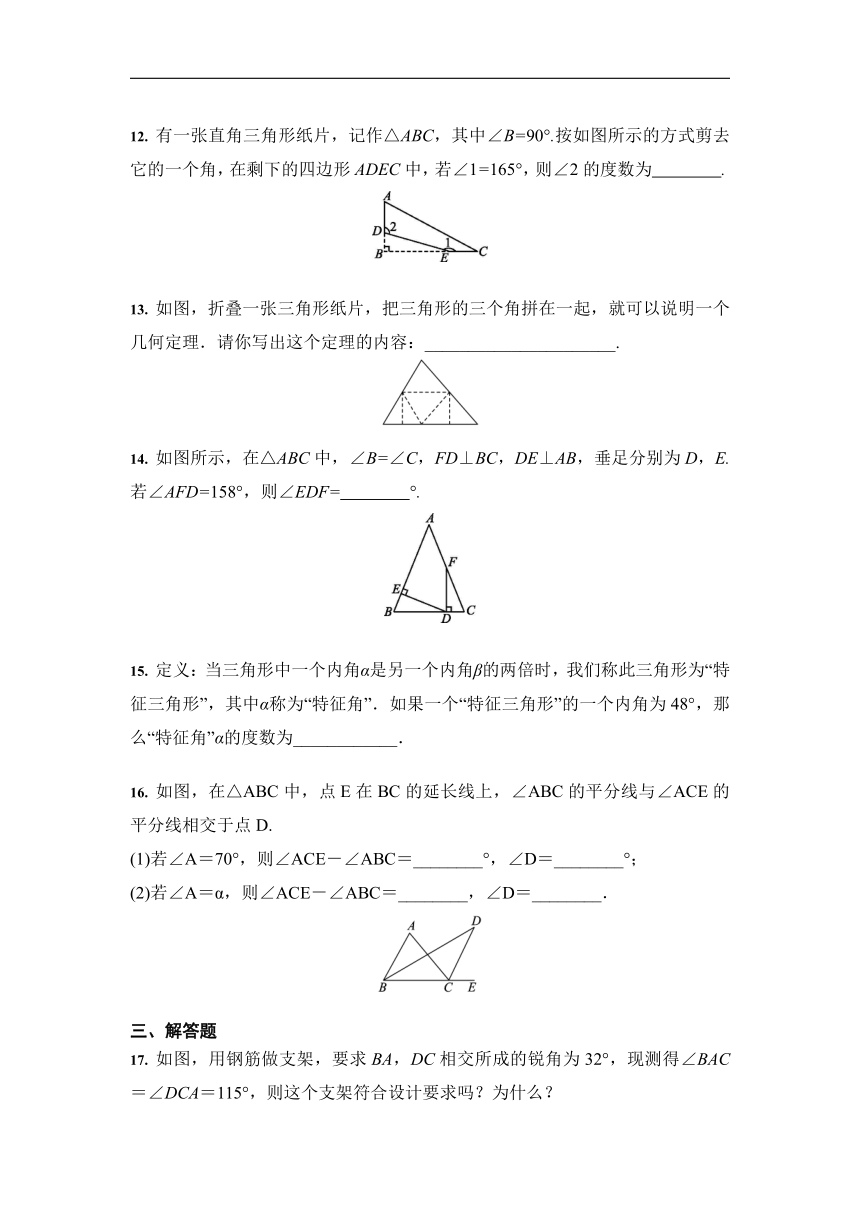
12. 有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图所示的方式剪去它的一个角,在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为 .?
13. 如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就可以说明一个几何定理.请你写出这个定理的内容:______________________.
14. 如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E.若∠AFD=158°,则∠EDF= °.
15. 定义:当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么“特征角”α的度数为____________.
16. 如图,在△ABC中,点E在BC的延长线上,∠ABC的平分线与∠ACE的平分线相交于点D.
(1)若∠A=70°,则∠ACE-∠ABC=________°,∠D=________°;
(2)若∠A=α,则∠ACE-∠ABC=________,∠D=________.
三、解答题
17. 如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么?
18. 如图,在△ABC中,AD是BC边上的高,E是AB上一点,CE交AD于点M,且∠DCM=∠MAE.
求证:△ACE是直角三角形.
19. 在△ABC中,∠B=55°,且3∠A=∠B+∠C,求∠A和∠C的度数.
20. 如图,在△ABC中,CD,BE分别是AB,AC边上的高,BE,CD相交于点O.
(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)求证:∠BOC+∠A=180°.
人教版 八年级数学上册 11.2 与三角形有关的角 同步培优训练-答案
一、选择题
1. 【答案】A
2. 【答案】B
3. 【答案】B 又∵∠A-∠B=50°,∴2∠A=140°.
∴∠A=70°.
4. 【答案】B ∴∠CFD=∠AFE=55°.
∴∠ACB=∠D+∠CFD=15°+55°=70°.
5. 【答案】 C
6. 【答案】C 由题意,得2x+3x+7x=180°,解得x=15°.
∴7x=105°.
7. 【答案】C ∴∠ACB=180°-∠A-∠ABC=78°.
∵∠ABC,∠ACB的平分线分别为BE,CD,
∴∠FBC=∠ABC=21°,∠FCB=∠ACB=39°,
∴∠BFC=180°-∠FBC-∠FCB=120°.
故选C.
8. 【答案】D ∴∠DBC=∠ABD=30°,∠ABC=2∠ABD=2×30°=60°.
∴∠ACB=180°-∠A-∠ABC=40°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
∴∠BDC=180°-∠DCB-∠DBC=130°.
9. 【答案】B
10. 【答案】A
二、填空题
11. 【答案】 105°
12. 【答案】105° 所以∠1+∠2=360°-90°=270°.
因为∠1=165°,
所以∠2的度数为105°.
13. 【答案】三角形三个内角的和等于180°
14. 【答案】68 ∴∠CFD=180°-∠AFD=180°-158°=22°.
∵FD⊥BC,
∴∠FDC=90°.
∴∠C=180°-∠FDC-∠CFD=180°-90°-22°=68°.
∵∠B=∠C,DE⊥AB,
∴∠EDB=180°-∠B-∠DEB=180°-68°-90°=22°.
∴∠EDF=180°-90°-22°=68°.
15. 【答案】48°或96°或88° 当β=48°时,则“特征角”α=2×48°=96°;
当第三个角为48°时,α+α+48°=180°,解得α=88°.
综上所述,“特征角”α的度数为48°或96°或88°.
16. 【答案】(1)70 35 (2)α α
三、解答题
17. 【答案】
解:这个支架不符合设计要求.
理由:如图,延长BA,DC交于点E.
∵∠BAC=∠DCA=115°,
∴∠EAC=∠ECA=65°.
∴∠E=180°-∠EAC-∠ECA=50°.
∵要求BA,DC相交所成的锐角为32°,
∴这个支架不符合设计要求.
18. 【答案】
证明:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠DCM=∠MAE,∠CMD=∠AME,
∴∠AEC=∠ADC=90°.
∴△ACE是直角三角形.
19. 【答案】
解:∵在△ABC中,∠A+∠B+∠C=180°,3∠A=∠B+∠C,
∴4∠A=180°,
解得∠A=45°.
∵∠B=55°,∴∠C=180°-45°-55°=80°.
20. 【答案】
解:(1)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠BEC=90°.
∵∠ABC=50°,∠ACB=60°.
∴∠BCO=40°,∠CBO=30°.
∴∠BOC=180°-40°-30°=110°.
(2)证明:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠BEC=90°.
∴∠ABE=90°-∠A.
∴∠BOC=∠ABE+∠BDC=90°-∠A+90°=180°-∠A.
∴∠BOC+∠A=180°.
一、选择题
1. 已知在△ABC中,∠A=70°,∠B=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
2. 在△ABC中,∠A,∠C与∠B处的外角的度数如图所示,则x的值是( )
A.80 B.70 C.65 D.60
3. 在Rt△ABC中,∠C=90°,∠A-∠B=50°,则∠A的度数为( )
A.80° B.70° C.60° D.50°
4. 如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A.65° B.70° C.75° D.85°
5. 一个三角形三个内角的度数之比为2∶3∶4,这个三角形是( )
A. 直角三角形 B. 等腰三角形
C. 锐角三角形 D. 钝角三角形
6. 若三角形的三个内角的度数之比为2∶3∶7,则这个三角形的最大内角是( )
A.75° B.90° C.105° D.120°
7. 如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为 ( )
A.118° B.119° C.120° D.121°
8. 如图,在△ABC中,D是∠ABC和∠ACB的平分线的交点,∠A=80°,∠ABD=30°,则∠BDC的度数为( )
A.100° B.110° C.120° D.130°
9. 如图,把△ABC沿DE折叠,当点A落在四边形BCED内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,这个关系是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
10. 如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是 ( )
A.x=y+z B.x=y-z C.x=z-y D.x+y+z=180
二、填空题
11. 如图所示,在△ABC中,∠A=45°,∠B=60°,则外角∠ACD= . ?
12. 有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图所示的方式剪去它的一个角,在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为 .?
13. 如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就可以说明一个几何定理.请你写出这个定理的内容:______________________.
14. 如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E.若∠AFD=158°,则∠EDF= °.
15. 定义:当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么“特征角”α的度数为____________.
16. 如图,在△ABC中,点E在BC的延长线上,∠ABC的平分线与∠ACE的平分线相交于点D.
(1)若∠A=70°,则∠ACE-∠ABC=________°,∠D=________°;
(2)若∠A=α,则∠ACE-∠ABC=________,∠D=________.
三、解答题
17. 如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么?
18. 如图,在△ABC中,AD是BC边上的高,E是AB上一点,CE交AD于点M,且∠DCM=∠MAE.
求证:△ACE是直角三角形.
19. 在△ABC中,∠B=55°,且3∠A=∠B+∠C,求∠A和∠C的度数.
20. 如图,在△ABC中,CD,BE分别是AB,AC边上的高,BE,CD相交于点O.
(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)求证:∠BOC+∠A=180°.
人教版 八年级数学上册 11.2 与三角形有关的角 同步培优训练-答案
一、选择题
1. 【答案】A
2. 【答案】B
3. 【答案】B 又∵∠A-∠B=50°,∴2∠A=140°.
∴∠A=70°.
4. 【答案】B ∴∠CFD=∠AFE=55°.
∴∠ACB=∠D+∠CFD=15°+55°=70°.
5. 【答案】 C
6. 【答案】C 由题意,得2x+3x+7x=180°,解得x=15°.
∴7x=105°.
7. 【答案】C ∴∠ACB=180°-∠A-∠ABC=78°.
∵∠ABC,∠ACB的平分线分别为BE,CD,
∴∠FBC=∠ABC=21°,∠FCB=∠ACB=39°,
∴∠BFC=180°-∠FBC-∠FCB=120°.
故选C.
8. 【答案】D ∴∠DBC=∠ABD=30°,∠ABC=2∠ABD=2×30°=60°.
∴∠ACB=180°-∠A-∠ABC=40°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
∴∠BDC=180°-∠DCB-∠DBC=130°.
9. 【答案】B
10. 【答案】A
二、填空题
11. 【答案】 105°
12. 【答案】105° 所以∠1+∠2=360°-90°=270°.
因为∠1=165°,
所以∠2的度数为105°.
13. 【答案】三角形三个内角的和等于180°
14. 【答案】68 ∴∠CFD=180°-∠AFD=180°-158°=22°.
∵FD⊥BC,
∴∠FDC=90°.
∴∠C=180°-∠FDC-∠CFD=180°-90°-22°=68°.
∵∠B=∠C,DE⊥AB,
∴∠EDB=180°-∠B-∠DEB=180°-68°-90°=22°.
∴∠EDF=180°-90°-22°=68°.
15. 【答案】48°或96°或88° 当β=48°时,则“特征角”α=2×48°=96°;
当第三个角为48°时,α+α+48°=180°,解得α=88°.
综上所述,“特征角”α的度数为48°或96°或88°.
16. 【答案】(1)70 35 (2)α α
三、解答题
17. 【答案】
解:这个支架不符合设计要求.
理由:如图,延长BA,DC交于点E.
∵∠BAC=∠DCA=115°,
∴∠EAC=∠ECA=65°.
∴∠E=180°-∠EAC-∠ECA=50°.
∵要求BA,DC相交所成的锐角为32°,
∴这个支架不符合设计要求.
18. 【答案】
证明:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠DCM=∠MAE,∠CMD=∠AME,
∴∠AEC=∠ADC=90°.
∴△ACE是直角三角形.
19. 【答案】
解:∵在△ABC中,∠A+∠B+∠C=180°,3∠A=∠B+∠C,
∴4∠A=180°,
解得∠A=45°.
∵∠B=55°,∴∠C=180°-45°-55°=80°.
20. 【答案】
解:(1)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠BEC=90°.
∵∠ABC=50°,∠ACB=60°.
∴∠BCO=40°,∠CBO=30°.
∴∠BOC=180°-40°-30°=110°.
(2)证明:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠BEC=90°.
∴∠ABE=90°-∠A.
∴∠BOC=∠ABE+∠BDC=90°-∠A+90°=180°-∠A.
∴∠BOC+∠A=180°.
