第一章 丰富的图形世界单元检测试题(含答案)
文档属性
| 名称 | 第一章 丰富的图形世界单元检测试题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师版七年级上学期第一章单元检测试题
一、单选题(共12题;共24分)
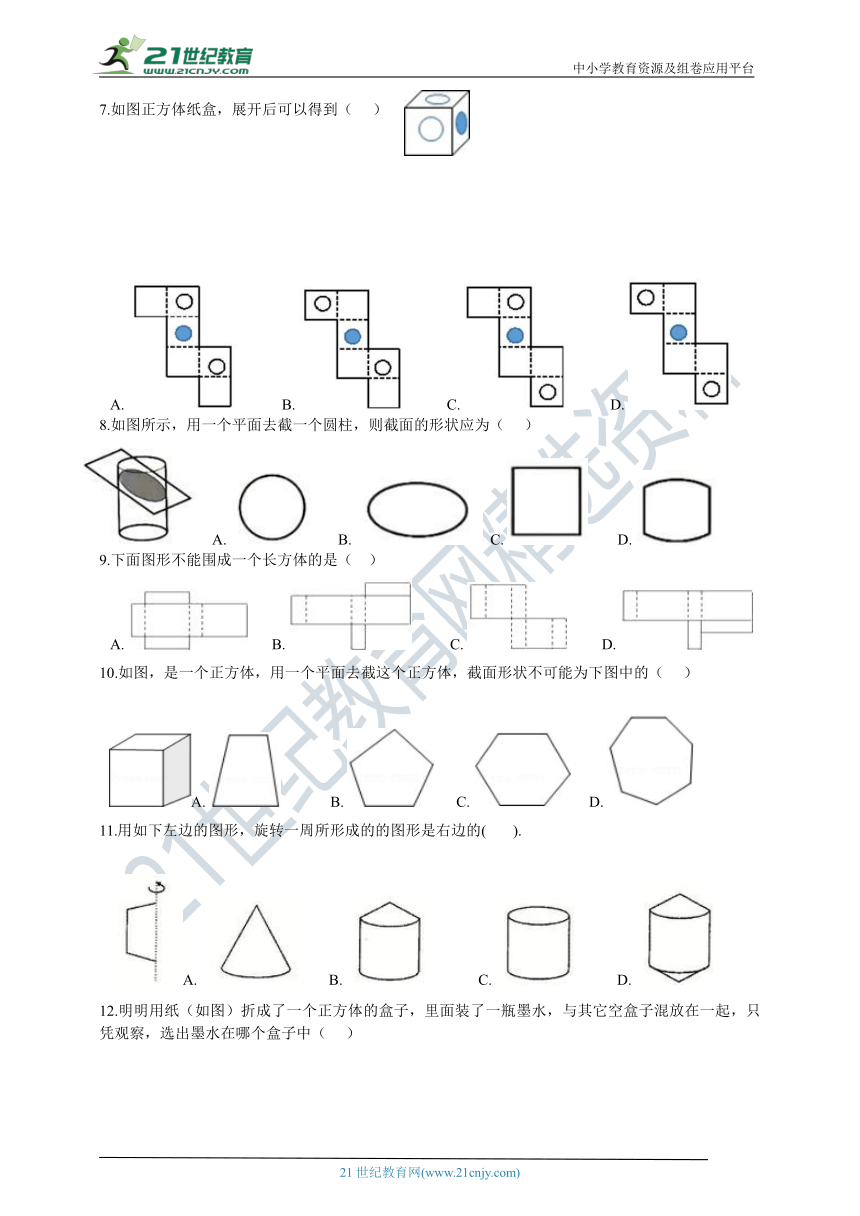
1.下列图形不是正方体的表面展开图的是(?? )
A.?B.?C.???????????????D.?
2.一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和“崇”相对的面上写的汉字是(?? )
?
A.?低????????????????????????????????????B.?碳??????????????????????????????C.?生???????????????????????????????????D.?活
3.有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,你不能选择图中 , , , 中的(?? )位置接正方形.
A.????????????????????????????????????B.???????????????????????????????????C.?????????????????????????????????????D.?
4.已知某多面体的平面展开图如图所示,其中是三棱柱的有(???? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5.下列说法,不正确的是(?? )
A.?用一个平面去截长方体,截面可能是正方形
B.?用一个平面去截正方体,截面可能是等腰梯形
C.?用一个平面去截圆锥,截面可能是梯形
D.?用一个平面去截正方体,截面可能是等边三角形
6.下面的几何体,是由A、B、C、D中的哪个图旋转一周形成的(? )
????????????? ?????
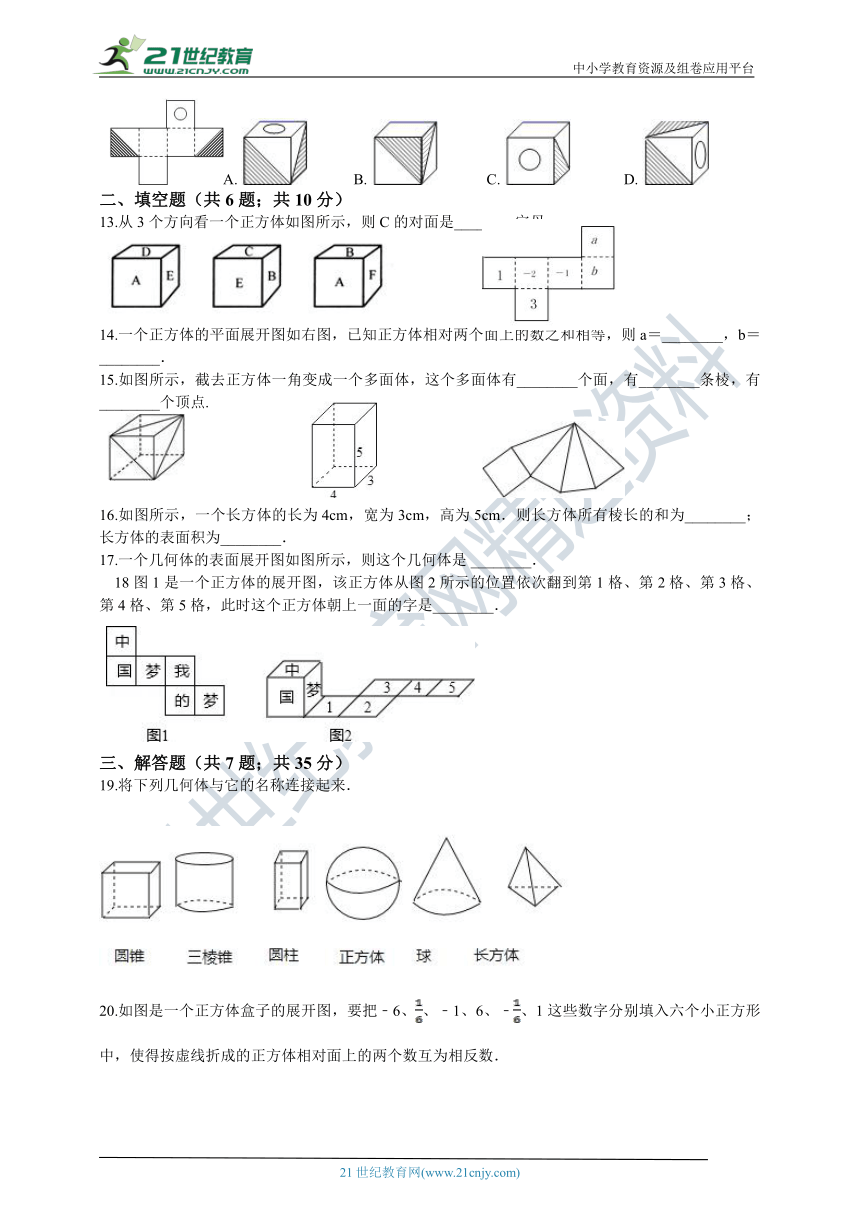
7.如图正方体纸盒,展开后可以得到(? ??)
A.?????????????B.????????????C.????????????D.?
8.如图所示,用一个平面去截一个圆柱,则截面的形状应为(??? )
A.???????B.???C.?????????D.?
9.下面图形不能围成一个长方体的是(?? )
A.???????B.???????????C.??????????D.?
10.如图,是一个正方体,用一个平面去截这个正方体,截面形状不可能为下图中的( ???)
A.??????????????B.??? C.??????D.?
11.用如下左边的图形,旋转一周所形成的的图形是右边的(? ????).
A.????????B.??????????????C.????????????D.?
12.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中(??? )
?
A.?????????????B.??????????????C.???????????????D.?
二、填空题(共6题;共10分)
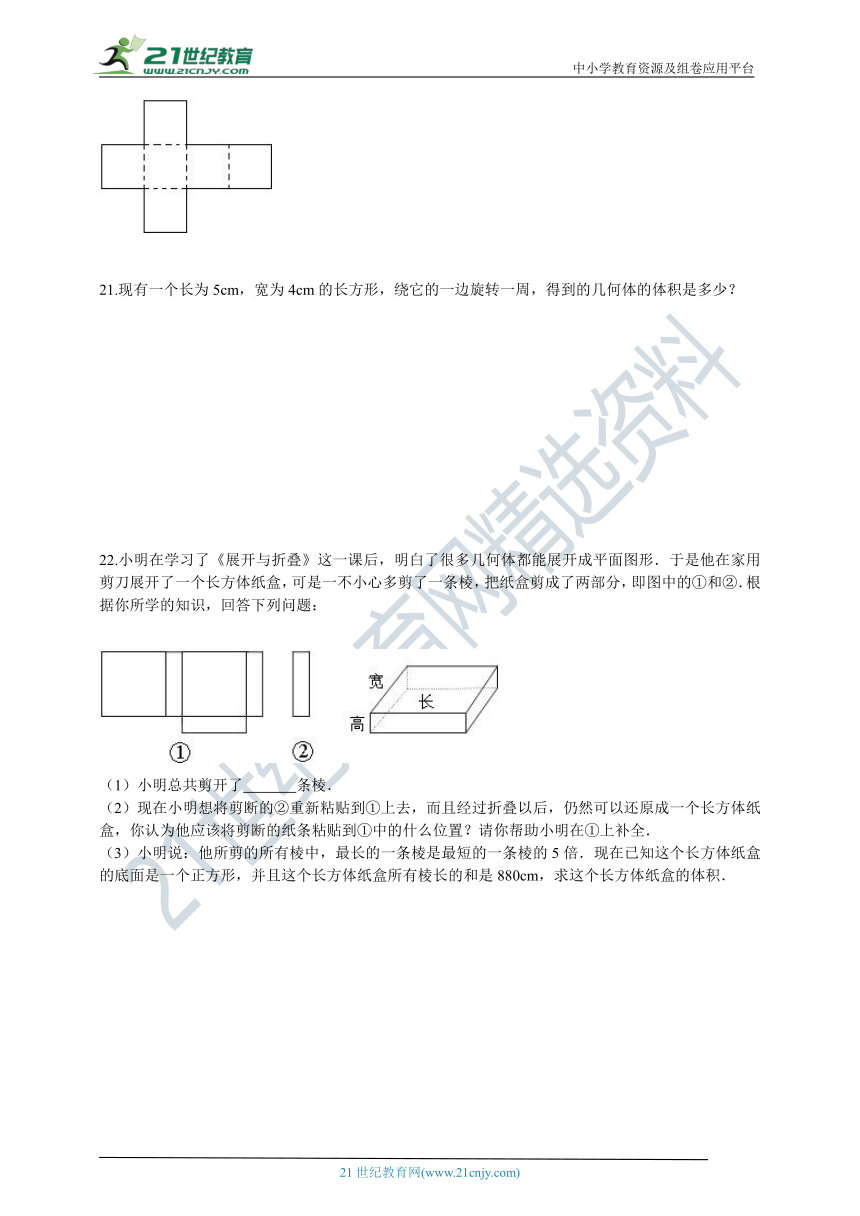
13.从3个方向看一个正方体如图所示,则C的对面是________字母.
14.一个正方体的平面展开图如右图,已知正方体相对两个面上的数之和相等,则a=________,b=________.
15.如图所示,截去正方体一角变成一个多面体,这个多面体有________个面,有________条棱,有________个顶点.
16.如图所示,一个长方体的长为4cm,宽为3cm,高为5cm.则长方体所有棱长的和为________;长方体的表面积为________.
17.一个几何体的表面展开图如图所示,则这个几何体是?________.
?18图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是________.
三、解答题(共7题;共35分)
19.将下列几何体与它的名称连接起来.
20.如图是一个正方体盒子的展开图,要把﹣6、、﹣1、6、﹣、1这些数字分别填入六个小正方形中,使得按虚线折成的正方体相对面上的两个数互为相反数.
21.现有一个长为5cm,宽为4cm的长方形,绕它的一边旋转一周,得到的几何体的体积是多少?
22.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了?? ? ? ? ?条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
23.如图,一个正五棱柱的底面边长为2cm,高为4cm.
(1)这个棱柱共有多少个面?计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数.
?
24.把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
颜色 红 黄 蓝 白 紫 绿
花的朵数 1 2 3 4 5 6
现将上述大小相同,颜色.花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问:长方体的下底面共有多少朵花?
25.回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
?
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 A
3.【答案】 A
4.【答案】 B
5.【答案】 C
6.【答案】 A
7.【答案】 A
8.【答案】 B
9.【答案】D
10.【答案】 D
11.【答案】 D
12.【答案】 B
二、填空题
13.【答案】 A
14.【答案】 -3;2
15.【答案】 7;12;7
16.【答案】48cm;94cm2
17.【答案】四棱锥
18.【答案】 我
三、解答题
19.【答案】 解:如图所示:
20.【答案】 解:如图:
?
21.【答案】解:以宽为旋转轴,V=π×52×4=100π;以长为旋转轴,V=π×42×5=80π
22.【答案】 解(1)小明共剪了8条棱,
故答案为:8.
(2)如图,四种情况.
?
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为acm,则长与宽相等为5acm,
∵长方体纸盒所有棱长的和是880cm,
∴4(a+5a+5a)=880,解得a=20cm,
∴这个长方体纸盒的体积为:20×100×100=200000立方厘米.
23.【答案】 解:(1)侧面有5个,底面有2个,共有5+2=7个面;侧面积:2×5×4=40(cm2).(2)顶点共10个,棱共有15条;(3)n棱柱的顶点数2n;面数n+2;棱的条数3n.
24.【答案】解:因为长方体是由大小相同,颜色.花朵分布也完全相同的四个正方体拼成的,所以根据图中与红色的面相邻的有紫.白.蓝.黄色的面,可以确定出每个小正方体红色面对绿色面,与黄色面相邻的有白.蓝.红.绿色的面,所以黄色面对紫色面,与蓝色面相邻的有黄.红.绿.紫色的面,所以蓝色面对白色面,所以可知长方体下底面从左到右依次是紫色.黄色.绿色.白色,再由表格中花的朵数可知共有 5+2+6+4=17(朵)
25.【答案】 解:(1)图甲折叠后底面和侧面都是长方形,所以是长方体;图乙折叠后底面是五边形,侧面是三角形,实际上是五棱锥的展开图,所以是五棱锥.(2)甲:f=6,e=12,v=8,f+v﹣e=2;乙:f=6,e=10,v=6,f+v﹣e=2;规律:顶点数+面数﹣棱数=2.(3)设这个多面体的面数为x,则x+x+8﹣50=2解得x=22.
_21?????????è?????(www.21cnjy.com)_
北师版七年级上学期第一章单元检测试题
一、单选题(共12题;共24分)
1.下列图形不是正方体的表面展开图的是(?? )
A.?B.?C.???????????????D.?
2.一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和“崇”相对的面上写的汉字是(?? )
?
A.?低????????????????????????????????????B.?碳??????????????????????????????C.?生???????????????????????????????????D.?活
3.有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,你不能选择图中 , , , 中的(?? )位置接正方形.
A.????????????????????????????????????B.???????????????????????????????????C.?????????????????????????????????????D.?
4.已知某多面体的平面展开图如图所示,其中是三棱柱的有(???? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5.下列说法,不正确的是(?? )
A.?用一个平面去截长方体,截面可能是正方形
B.?用一个平面去截正方体,截面可能是等腰梯形
C.?用一个平面去截圆锥,截面可能是梯形
D.?用一个平面去截正方体,截面可能是等边三角形
6.下面的几何体,是由A、B、C、D中的哪个图旋转一周形成的(? )
????????????? ?????
7.如图正方体纸盒,展开后可以得到(? ??)
A.?????????????B.????????????C.????????????D.?
8.如图所示,用一个平面去截一个圆柱,则截面的形状应为(??? )
A.???????B.???C.?????????D.?
9.下面图形不能围成一个长方体的是(?? )
A.???????B.???????????C.??????????D.?
10.如图,是一个正方体,用一个平面去截这个正方体,截面形状不可能为下图中的( ???)
A.??????????????B.??? C.??????D.?
11.用如下左边的图形,旋转一周所形成的的图形是右边的(? ????).
A.????????B.??????????????C.????????????D.?
12.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中(??? )
?
A.?????????????B.??????????????C.???????????????D.?
二、填空题(共6题;共10分)
13.从3个方向看一个正方体如图所示,则C的对面是________字母.
14.一个正方体的平面展开图如右图,已知正方体相对两个面上的数之和相等,则a=________,b=________.
15.如图所示,截去正方体一角变成一个多面体,这个多面体有________个面,有________条棱,有________个顶点.
16.如图所示,一个长方体的长为4cm,宽为3cm,高为5cm.则长方体所有棱长的和为________;长方体的表面积为________.
17.一个几何体的表面展开图如图所示,则这个几何体是?________.
?18图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是________.
三、解答题(共7题;共35分)
19.将下列几何体与它的名称连接起来.
20.如图是一个正方体盒子的展开图,要把﹣6、、﹣1、6、﹣、1这些数字分别填入六个小正方形中,使得按虚线折成的正方体相对面上的两个数互为相反数.
21.现有一个长为5cm,宽为4cm的长方形,绕它的一边旋转一周,得到的几何体的体积是多少?
22.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了?? ? ? ? ?条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
23.如图,一个正五棱柱的底面边长为2cm,高为4cm.
(1)这个棱柱共有多少个面?计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数.
?
24.把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
颜色 红 黄 蓝 白 紫 绿
花的朵数 1 2 3 4 5 6
现将上述大小相同,颜色.花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问:长方体的下底面共有多少朵花?
25.回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
?
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 A
3.【答案】 A
4.【答案】 B
5.【答案】 C
6.【答案】 A
7.【答案】 A
8.【答案】 B
9.【答案】D
10.【答案】 D
11.【答案】 D
12.【答案】 B
二、填空题
13.【答案】 A
14.【答案】 -3;2
15.【答案】 7;12;7
16.【答案】48cm;94cm2
17.【答案】四棱锥
18.【答案】 我
三、解答题
19.【答案】 解:如图所示:
20.【答案】 解:如图:
?
21.【答案】解:以宽为旋转轴,V=π×52×4=100π;以长为旋转轴,V=π×42×5=80π
22.【答案】 解(1)小明共剪了8条棱,
故答案为:8.
(2)如图,四种情况.
?
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为acm,则长与宽相等为5acm,
∵长方体纸盒所有棱长的和是880cm,
∴4(a+5a+5a)=880,解得a=20cm,
∴这个长方体纸盒的体积为:20×100×100=200000立方厘米.
23.【答案】 解:(1)侧面有5个,底面有2个,共有5+2=7个面;侧面积:2×5×4=40(cm2).(2)顶点共10个,棱共有15条;(3)n棱柱的顶点数2n;面数n+2;棱的条数3n.
24.【答案】解:因为长方体是由大小相同,颜色.花朵分布也完全相同的四个正方体拼成的,所以根据图中与红色的面相邻的有紫.白.蓝.黄色的面,可以确定出每个小正方体红色面对绿色面,与黄色面相邻的有白.蓝.红.绿色的面,所以黄色面对紫色面,与蓝色面相邻的有黄.红.绿.紫色的面,所以蓝色面对白色面,所以可知长方体下底面从左到右依次是紫色.黄色.绿色.白色,再由表格中花的朵数可知共有 5+2+6+4=17(朵)
25.【答案】 解:(1)图甲折叠后底面和侧面都是长方形,所以是长方体;图乙折叠后底面是五边形,侧面是三角形,实际上是五棱锥的展开图,所以是五棱锥.(2)甲:f=6,e=12,v=8,f+v﹣e=2;乙:f=6,e=10,v=6,f+v﹣e=2;规律:顶点数+面数﹣棱数=2.(3)设这个多面体的面数为x,则x+x+8﹣50=2解得x=22.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
