2020-2021学年人教新版八年级数学上册《11.3 多边形及其内角和》高频易错题汇编(附解析)
文档属性
| 名称 | 2020-2021学年人教新版八年级数学上册《11.3 多边形及其内角和》高频易错题汇编(附解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11.3
多边形及其内角和
高频易错题汇编
一.选择题(共10小题)
1.下列结论正确的个数是( )个.
①1°=100分;②七棱柱有14个顶点;③两点之间线段最短;④各边相等的多边形是正多边形;⑤23xy是5次单项式.
A.1个
B.2个
C.3个
D.4个
2.下列图形中不具有稳定性的是( )
A.锐角三角形
B.长方形
C.直角三角形
D.等腰三角形
3.下列图形中具有稳定性的是( )
A.菱形
B.长方形
C.平行四边形
D.钝角三角形
4.下列结论正确的是( )
A.平行四边形是轴对称图形
B.菱形的对角线互相垂直且相等
C.正方形的对称轴有4条
D.矩形的对角线互相垂直
5.在平面中,下列说法正确的是( )
A.四个角相等的四边形是矩形
B.对角线垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.四边相等的四边形是正方形
6.当多边形的边数增加1时,它的内角和会( )
A.增加160°
B.增加180°
C.增加270°
D.增加360°
7.已知一个多边形的外角和比它的内角和少540°,则该多边形的边数为( )
A.7
B.8
C.9
D.10
8.下列说法中,正确的个数有( )
①同位角相等;
②三角形的高相交于三角形的内部;③三角形的一个外角大于任意一个内角;④一个多边形的边数每增加一条,这个多边形的内角和就增加180°;⑤两个角的两边分别平行,则这两个角相等.
A.0个
B.1个
C.2个
D.3个
9.如图,将四边形纸片ABCD沿MN折叠,若∠1+∠2=130°,则∠B+∠C=( )
A.115°
B.130°
C.135°
D.150°
10.若一个多边形的内角和等于1800度,则这个多边形是( )
A.十二边形
B.十边形
C.九边形
D.八边形
二.填空题(共5小题)
11.将一个正六边形纸片对折,并完全重合,那么得到的图形是
边形.
12.一个n边形的内角和是它外角和的6倍,则n=
.
13.已知一个多边形的每个外角都是24°,此多边形是
边形.
14.如图,蚂蚁点P出发,沿直线行走40米后左转30°,再沿直线行走40米,又左转30°,…;照此走下去,它第一次回到出发点P,一共行走的路程是
米.
15.如图,在正五边形ABCDE中,AC为对角线,以点A为圆心,AE为半径画圆弧交AC于点F,连结EF,则∠1的度数为
.
三.解答题(共5小题)
16.如图1.已知大圆的直径为16米,小圆的直径比大四的直径少(注:π取3)
(1)求小圆的周长;
(2)德强学校的操场上有一个五彩的奥运五环图案,是由5个与图1完全相同的圆环构成,若每两个环形相交的部分是曲边四边形,每个曲边四边形面积都是平方米,求这个五环图形的面积.
(3)在(2)的条件下,为了迎接11月1日在我校举行的全国“70节好课致敬新中国70年”观摩课活动,学校决定重新粉剧操场上的奥运五环,学校雇佣2个师傅和4个徒弟来完成这项任务(每名师傅每小时粉刷的面积相同,每个徒弟每小时粉剧的面积相同),已知1个师傅1小时粉刷的面积是师徒6人1小时粉刷面积的.工作2小时后,4个徒弟比两个师傅多粉刷24平方米,这时两个师傅因有其它任务离开,剩下的工作由4个徒弟完成,工作完成,学校每小时支付师傅工资270元,每小时支付徒弟工资150元,学校共支付工资多少元.
举例说明各边相等的多边形不一定是正多边形.
18.如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别交CD、AB于点E、F,且∠1与∠2互余,∠A与∠C有怎样的数量关系?为什么?
19.【知识回顾】:
如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD=
.
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB=
°.(直接写出答案)
(2)若∠A=70°,则∠DBC+∠ECB=
°.(直接写出答案)
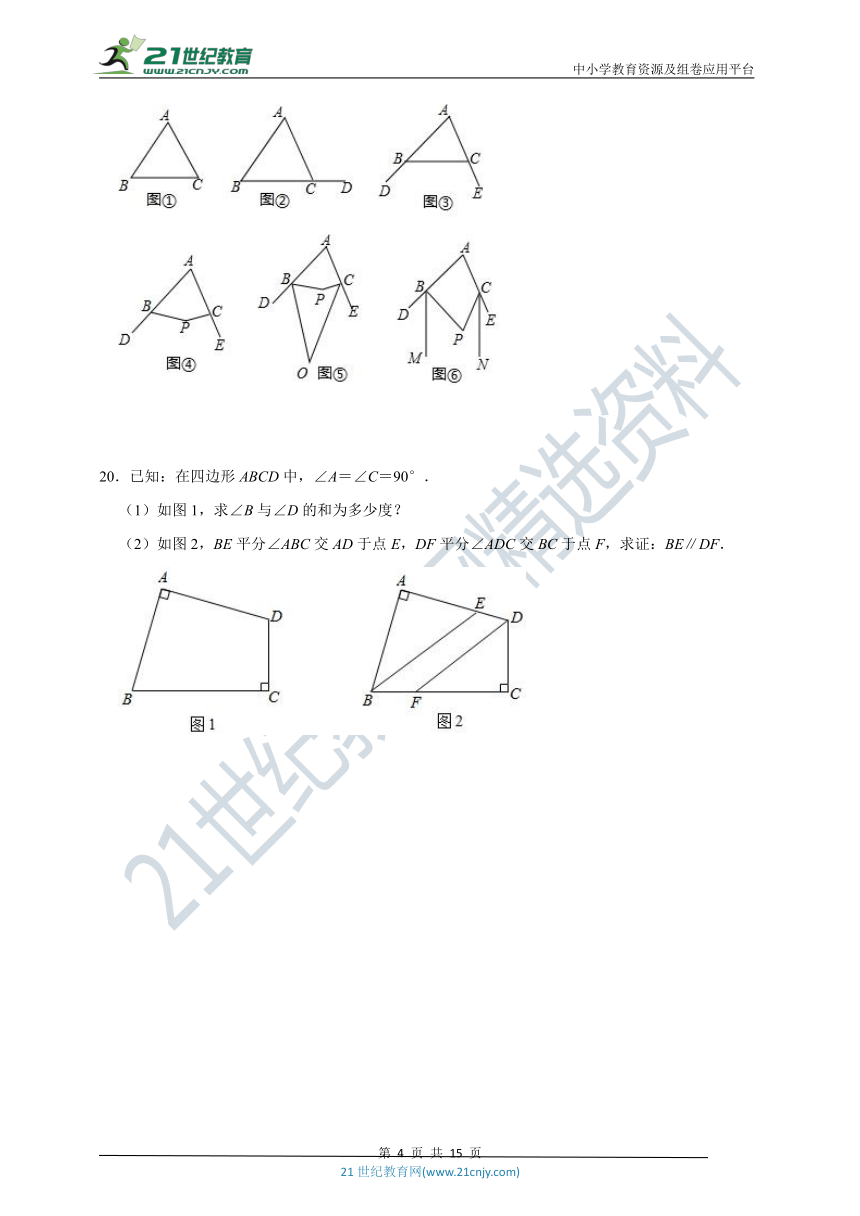
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP=
°.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
20.已知:在四边形ABCD中,∠A=∠C=90°.
(1)如图1,求∠B与∠D的和为多少度?
(2)如图2,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F,求证:BE∥DF.
人教新版八年级上学期《11.3
多边形及其内角和》2020年高频易错题集
参考答案与试题解析
一.选择题(共10小题)
1.下列结论正确的个数是( )个.
①1°=100分;②七棱柱有14个顶点;③两点之间线段最短;④各边相等的多边形是正多边形;⑤23xy是5次单项式.
A.1个
B.2个
C.3个
D.4个
【考点】单项式;认识立体图形;线段的性质:两点之间线段最短;多边形.
【分析】分别根据角的单位换算、棱柱的特征、线段的定义、正多边形的定义以及单项式的定义逐一判断即可.
【解答】解:①1°=60′,故①原说法错误;
②七棱柱有14个顶点,正确;
③两点之间线段最短,正确;
④各边、各角分别相等的多边形是正多边形,故④原说法错误;
⑤23xy是二次单项式,故⑤原说法错误;
∴正确的有:②③共2个.
2.下列图形中不具有稳定性的是( )
A.锐角三角形
B.长方形
C.直角三角形
D.等腰三角形
【考点】三角形的稳定性;多边形.
【分析】三角形具有稳定性,根据三角形的性质,四边形的性质可得答案.
【解答】解:长方形属于四边形,不具有稳定性,而三角形具有稳定性,故B符合题意;
故选:B.
3.下列图形中具有稳定性的是( )
A.菱形
B.长方形
C.平行四边形
D.钝角三角形
【考点】三角形的稳定性;多边形.
【分析】根据三角形具有稳定性解答.
【解答】解:菱形,长方形,平行四边形,钝角三角形中只有钝角三角形具有稳定性.
故选:D.
4.下列结论正确的是( )
A.平行四边形是轴对称图形
B.菱形的对角线互相垂直且相等
C.正方形的对称轴有4条
D.矩形的对角线互相垂直
【考点】多边形.
【分析】根据平行四边形,菱形,正方形,矩形的性质,结合选项进行判断即可.
【解答】解:A、平行四边形是中心对称图形,原说法错误,故本选项错误;
B、菱形的对角线互相垂直,但不相等,原说法错误,故本选项错误;
C、正方形既是中心对称图形又是轴对称图形,对称轴有4条,故本选项正确;
D、矩形的对角线相等,原说法错误,故本选项错误;
故选:C.
5.在平面中,下列说法正确的是( )
A.四个角相等的四边形是矩形
B.对角线垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.四边相等的四边形是正方形
【考点】多边形.
【分析】根据矩形、菱形、正方形的判定定理,即可解答.
【解答】解:A.四个角相等的四边形是矩形,正确;
B.对角线垂直的平行四边形是菱形,故错误;
C.对角线相等的平行四边形是矩形,故错误;
D.四边相等的四边形应是菱形,故错误;
故选:A.
6.当多边形的边数增加1时,它的内角和会( )
A.增加160°
B.增加180°
C.增加270°
D.增加360°
【考点】多边形内角与外角.
【分析】设原多边形边数是n,则新多边形的边数是n+1.根据多边形的内角和定理即可求得.
【解答】解:设原多边形边数是n,则n边形的内角和是(n﹣2)?180°,边数增加1,则新多边形的内角和是(n+1﹣2)?180°.
则(n+1﹣2)?180°﹣(n﹣2)?180°=180°.
故它的内角和增加180°.
故选:B.
7.已知一个多边形的外角和比它的内角和少540°,则该多边形的边数为( )
A.7
B.8
C.9
D.10
【考点】多边形内角与外角.
【分析】根据多边形的内角和公式(n﹣2)?180°,外角和等于360°列出方程求解即可.
【解答】解:设多边形的边数是n,
根据题意得,(n﹣2)?180°﹣360°=540°,
解得n=7.
故选:A.
8.下列说法中,正确的个数有( )
①同位角相等;
②三角形的高相交于三角形的内部;③三角形的一个外角大于任意一个内角;④一个多边形的边数每增加一条,这个多边形的内角和就增加180°;⑤两个角的两边分别平行,则这两个角相等.
A.0个
B.1个
C.2个
D.3个
【考点】同位角、内错角、同旁内角;三角形内角和定理;三角形的外角性质;多边形内角与外角.
【分析】根据同位角的定义、三角形内外角的关系、三角形垂心的定义及多边形内角和公式、平行线的性质逐一判断可得.
【解答】解:①只有两平行直线被第三条直线所截时,同位角才相等,故说法①错误;
②只有锐角三角形的三条高在三角形的内部,故说法②错误;
③三角形的一个外角大于任意一个和它不相邻的内角,故说法③错误;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°,此说法④正确;
⑤两个角的两边分别平行,则这两个角可能相等,也可能互补,故说法⑤错误;
正确的个数有1个,
故选:B.
9.如图,将四边形纸片ABCD沿MN折叠,若∠1+∠2=130°,则∠B+∠C=( )
A.115°
B.130°
C.135°
D.150°
【考点】多边形内角与外角.
【分析】先根据∠1+∠2=130°得出∠AMN+∠DNM的度数,再由四边形内角和定理即可得出结论.
【解答】解:∵∠1+∠2=130°,
∴∠AMN+∠DNM==115°.
∵∠A+∠D+(∠AMN+∠DNM)=360°,∠A+∠D+(∠B+∠C)=360°,
∴∠B+∠C=∠AMN+∠DNM=115°.
故选:A.
10.若一个多边形的内角和等于1800度,则这个多边形是( )
A.十二边形
B.十边形
C.九边形
D.八边形
【考点】多边形内角与外角.
【分析】根据多边形的内角和公式(n﹣2)?180°列式进行计算即可求解.
【解答】解:设多边形的边数是n,则
(n﹣2)?180=1800,
解得n=12,
所以这个多边形是十二边形.
故选:A.
二.填空题(共5小题)
11.将一个正六边形纸片对折,并完全重合,那么得到的图形是 四边形或五 边形.
【考点】多边形.
【分析】分折痕是对角线所在的直线与对边中点所在的直线两种情况讨论求解.
【解答】解:如图,①折痕是对角线所在的直线时,得到的图形是四边形,
②折痕是对边中点所在的直线时,得到的图形是五边形,
所以,得到的图形是四边形或五边形.
故答案为:四边形或五.
12.一个n边形的内角和是它外角和的6倍,则n= 14 .
【考点】多边形内角与外角.
【分析】利用多边形的内角和公式和外角和公式,根据一个n边形的内角和是其外角和的5倍列出方程求解即可.
【解答】解:多边形的外角和是360°,多边形的内角和是180°?(n﹣2),根据题意得:
180?(n﹣2)=360×6,
解得n=14.
故答案为:14.
13.已知一个多边形的每个外角都是24°,此多边形是 十五 边形.
【考点】多边形内角与外角.
【分析】任何多边形的外角和是360°.用外角和除以每个外角的度数即可得到边数.
【解答】解:360°÷24°=15.
故这个多边形是十五边形.
故答案为:十五.
14.如图,蚂蚁点P出发,沿直线行走40米后左转30°,再沿直线行走40米,又左转30°,…;照此走下去,它第一次回到出发点P,一共行走的路程是 480 米.
【考点】多边形内角与外角.
【分析】根据题意,蚂蚁走过的路程是正多边形,先用360°除以30°求出边数,然后再乘以40米即可.
【解答】解:∵蚂蚁每次都是沿直线前进40米后向左转30°,
∴它走过的图形是正多边形,
∴边数n=360°÷30°=12,
∴它第一次回到出发点P时,一共走了12×40=480(米).
故答案为:480.
15.如图,在正五边形ABCDE中,AC为对角线,以点A为圆心,AE为半径画圆弧交AC于点F,连结EF,则∠1的度数为 54° .
【考点】多边形内角与外角.
【分析】根据五边形的内角和公式求出∠ABC,根据等腰三角形的性质,三角形内角和的定理计算∠BAC,再求∠CAE,最后求出∠1即可.
【解答】解:∵五边形ABCDE是正五边形,
∴∠EAB=∠ABC==108°,
∵BA=BC,
∴∠BAC=∠BCA==36°,
∴∠EAF=108°﹣36°=72°,
∵以点A为圆心,AE为半径画圆弧交AC于点F,
∴AE=AF,
∴∠1==54°.
故答案为:54°.
三.解答题(共5小题)
16.如图1.已知大圆的直径为16米,小圆的直径比大四的直径少(注:π取3)
(1)求小圆的周长;
(2)德强学校的操场上有一个五彩的奥运五环图案,是由5个与图1完全相同的圆环构成,若每两个环形相交的部分是曲边四边形,每个曲边四边形面积都是平方米,求这个五环图形的面积.
(3)在(2)的条件下,为了迎接11月1日在我校举行的全国“70节好课致敬新中国70年”观摩课活动,学校决定重新粉剧操场上的奥运五环,学校雇佣2个师傅和4个徒弟来完成这项任务(每名师傅每小时粉刷的面积相同,每个徒弟每小时粉剧的面积相同),已知1个师傅1小时粉刷的面积是师徒6人1小时粉刷面积的.工作2小时后,4个徒弟比两个师傅多粉刷24平方米,这时两个师傅因有其它任务离开,剩下的工作由4个徒弟完成,工作完成,学校每小时支付师傅工资270元,每小时支付徒弟工资150元,学校共支付工资多少元.
【考点】认识平面图形;多边形.
【分析】(1)先计算小圆的直径,根据周长公式可得结论;
(2)理解曲边四边形是哪个图形,根据5×一个圆环的面积﹣8个曲边四边形的面积,可解答;
(3)先设1个徒弟每小时刷墙x米2,则1个师傅每小时刷墙(2x﹣6)米2,根据1个师傅1小时粉刷的面积是师徒6人1小时粉刷而积的,列方程可得师傅和徒弟的工作效率,根据已知计算徒弟工作总时间,和每小时的工资可得结论.
【解答】解:(1)由题意得:小圆的直径为:(1﹣)×16=14(米),
则小圆的周长为:π×14=3×14=42(米),
答:小圆的周长是42米;
(2)[5×﹣5×]﹣8×,
=5×3×15﹣9,
=216(米2),
答:这个五环图形的面积是216米2;
(3)设1个徒弟每小时刷墙x米2,则1个师傅每小时刷墙(2x﹣6)米2,
由题意得:2x﹣6=,
解得:x=12,
2x﹣6=2×12﹣6=18,
即设1个徒弟每小时刷墙12米2,则1个师傅每小时刷墙18米2,
=1,
即设4个徒弟干了3个小时,2个师傅干了2个小时,
3×150×4+2×270×2=2880(元),
答:学校共支付工资2880元.
17.举例说明各边相等的多边形不一定是正多边形.
【考点】多边形.
【分析】菱形的各边相等,但菱形不是正多边形.
【解答】解:各边相等的多边形不一定是正多边形,例如菱形的各边相等,但菱形不是正多边形.
18.如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别交CD、AB于点E、F,且∠1与∠2互余,∠A与∠C有怎样的数量关系?为什么?
【考点】三角形内角和定理;多边形内角与外角.
【分析】先求出∠1+∠2=90°,再求出∠ABC=2∠2,∠ADC=2∠1,即可求出∠ABC+∠ADC=2(∠1+∠2)=2×90°=180°,最后可以求出∠A+∠C=180°.
【解答】解:∠A+∠C=180°,理由如下:
∵∠1与∠2互余,
∴∠1+∠2=90°,
∵BE、DF分别平分∠ABC、∠ADC,
∴∠ABC=2∠2,∠ADC=2∠1,
∴∠ABC+∠ADC=2(∠1+∠2)=2×90°=180°,
∵∠A+∠ABC+∠C+∠ADC=360°,
∴∠A+∠C=180°.
19.【知识回顾】:
如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD= ∠A+∠B .
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB= 80 °.(直接写出答案)
(2)若∠A=70°,则∠DBC+∠ECB= 250 °.(直接写出答案)
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP= 220 °.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
【考点】平行线的判定;三角形内角和定理;三角形的外角性质;多边形内角与外角.
【分析】【知识回顾】
根据三角形的内角和定理和平角的定义可得结论;
【初步运用】
(1)根据三角形的外角等于与它不相邻的两个内角的和列式可得结论;
(2)根据三角形的内角和得:∠ABC+∠ACB=110°,由两个平角的和可得结论;
【拓展延伸】
(1)连接AP,根据三角形内角和定理的推论可得等式,将两个等式相加可得结论;
(2)如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,综合可得结论;
(3)如图⑥,作辅助线,构建三角形PQC,根据(1)的结论得:∠DBP+∠ECP=∠A+∠BPC,和角平分线的定义,证明∠MBP=∠PQC,可得结论.
【解答】解:【知识回顾】
∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠B;
故答案为:∠A+∠B;
【初步运用】
(1)∵∠DBC=∠A+∠ACB,∠A=70°,∠DBC=150°,
∴∠ACB=∠DBC﹣∠A=150°﹣70°=80°;
故答案为:80;
(2)∵∠A=70°,
∴∠ABC+∠ACB=110°,
∴∠DBC+∠ECB=360°﹣110°=250°,
故答案为:250;
【拓展延伸】
(1)如图④,连接AP,∵∠DBP=∠BAP+∠APB,∠ECP=∠CAP+∠APC,
∴∠DBP+∠ECP=∠BAP+∠APB+∠CAP+∠APC=∠BAC+∠BPC,
∵∠BAC=70°,∠BPC=150°,
∴∠DBP+∠ECP=∠BAC+∠BPC=70°+150°=220°,
故答案为:220;
(2)∠A和∠P之间的数量关系是:∠P=∠A+80°,
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=40°,
∴∠P=∠A+80°;
(3)证明:如图,延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN.
20.已知:在四边形ABCD中,∠A=∠C=90°.
(1)如图1,求∠B与∠D的和为多少度?
(2)如图2,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F,求证:BE∥DF.
【考点】平行线的判定;三角形内角和定理;多边形内角与外角.
【分析】(1)根据四边形内角和定理得出∠B+∠D=180°;
(2)首先根据四边形内角和定理得出∠ABC+∠ADC=180°,进而利用角平分线的性质得出∠ABE+∠EDF=90°,即可得出∠AEB=∠ADF,利用平行线的判定得出即可.
【解答】(1)解:∵∠A=∠C=90°,
∴∠B+∠D+∠A+∠C=(4﹣2)×180°=360°,
∴∠B+∠D=360°﹣∠A﹣∠C=180°;
即∠B与∠D的和为180度;
(2)证明:∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°﹣∠A﹣∠C=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE+∠EDF=90°,
∵∠ABE+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.3
多边形及其内角和
高频易错题汇编
一.选择题(共10小题)
1.下列结论正确的个数是( )个.
①1°=100分;②七棱柱有14个顶点;③两点之间线段最短;④各边相等的多边形是正多边形;⑤23xy是5次单项式.
A.1个
B.2个
C.3个
D.4个
2.下列图形中不具有稳定性的是( )
A.锐角三角形
B.长方形
C.直角三角形
D.等腰三角形
3.下列图形中具有稳定性的是( )
A.菱形
B.长方形
C.平行四边形
D.钝角三角形
4.下列结论正确的是( )
A.平行四边形是轴对称图形
B.菱形的对角线互相垂直且相等
C.正方形的对称轴有4条
D.矩形的对角线互相垂直
5.在平面中,下列说法正确的是( )
A.四个角相等的四边形是矩形
B.对角线垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.四边相等的四边形是正方形
6.当多边形的边数增加1时,它的内角和会( )
A.增加160°
B.增加180°
C.增加270°
D.增加360°
7.已知一个多边形的外角和比它的内角和少540°,则该多边形的边数为( )
A.7
B.8
C.9
D.10
8.下列说法中,正确的个数有( )
①同位角相等;
②三角形的高相交于三角形的内部;③三角形的一个外角大于任意一个内角;④一个多边形的边数每增加一条,这个多边形的内角和就增加180°;⑤两个角的两边分别平行,则这两个角相等.
A.0个
B.1个
C.2个
D.3个
9.如图,将四边形纸片ABCD沿MN折叠,若∠1+∠2=130°,则∠B+∠C=( )
A.115°
B.130°
C.135°
D.150°
10.若一个多边形的内角和等于1800度,则这个多边形是( )
A.十二边形
B.十边形
C.九边形
D.八边形
二.填空题(共5小题)
11.将一个正六边形纸片对折,并完全重合,那么得到的图形是
边形.
12.一个n边形的内角和是它外角和的6倍,则n=
.
13.已知一个多边形的每个外角都是24°,此多边形是
边形.
14.如图,蚂蚁点P出发,沿直线行走40米后左转30°,再沿直线行走40米,又左转30°,…;照此走下去,它第一次回到出发点P,一共行走的路程是
米.
15.如图,在正五边形ABCDE中,AC为对角线,以点A为圆心,AE为半径画圆弧交AC于点F,连结EF,则∠1的度数为
.
三.解答题(共5小题)
16.如图1.已知大圆的直径为16米,小圆的直径比大四的直径少(注:π取3)
(1)求小圆的周长;
(2)德强学校的操场上有一个五彩的奥运五环图案,是由5个与图1完全相同的圆环构成,若每两个环形相交的部分是曲边四边形,每个曲边四边形面积都是平方米,求这个五环图形的面积.
(3)在(2)的条件下,为了迎接11月1日在我校举行的全国“70节好课致敬新中国70年”观摩课活动,学校决定重新粉剧操场上的奥运五环,学校雇佣2个师傅和4个徒弟来完成这项任务(每名师傅每小时粉刷的面积相同,每个徒弟每小时粉剧的面积相同),已知1个师傅1小时粉刷的面积是师徒6人1小时粉刷面积的.工作2小时后,4个徒弟比两个师傅多粉刷24平方米,这时两个师傅因有其它任务离开,剩下的工作由4个徒弟完成,工作完成,学校每小时支付师傅工资270元,每小时支付徒弟工资150元,学校共支付工资多少元.
举例说明各边相等的多边形不一定是正多边形.
18.如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别交CD、AB于点E、F,且∠1与∠2互余,∠A与∠C有怎样的数量关系?为什么?
19.【知识回顾】:
如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD=
.
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB=
°.(直接写出答案)
(2)若∠A=70°,则∠DBC+∠ECB=
°.(直接写出答案)
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP=
°.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
20.已知:在四边形ABCD中,∠A=∠C=90°.
(1)如图1,求∠B与∠D的和为多少度?
(2)如图2,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F,求证:BE∥DF.
人教新版八年级上学期《11.3
多边形及其内角和》2020年高频易错题集
参考答案与试题解析
一.选择题(共10小题)
1.下列结论正确的个数是( )个.
①1°=100分;②七棱柱有14个顶点;③两点之间线段最短;④各边相等的多边形是正多边形;⑤23xy是5次单项式.
A.1个
B.2个
C.3个
D.4个
【考点】单项式;认识立体图形;线段的性质:两点之间线段最短;多边形.
【分析】分别根据角的单位换算、棱柱的特征、线段的定义、正多边形的定义以及单项式的定义逐一判断即可.
【解答】解:①1°=60′,故①原说法错误;
②七棱柱有14个顶点,正确;
③两点之间线段最短,正确;
④各边、各角分别相等的多边形是正多边形,故④原说法错误;
⑤23xy是二次单项式,故⑤原说法错误;
∴正确的有:②③共2个.
2.下列图形中不具有稳定性的是( )
A.锐角三角形
B.长方形
C.直角三角形
D.等腰三角形
【考点】三角形的稳定性;多边形.
【分析】三角形具有稳定性,根据三角形的性质,四边形的性质可得答案.
【解答】解:长方形属于四边形,不具有稳定性,而三角形具有稳定性,故B符合题意;
故选:B.
3.下列图形中具有稳定性的是( )
A.菱形
B.长方形
C.平行四边形
D.钝角三角形
【考点】三角形的稳定性;多边形.
【分析】根据三角形具有稳定性解答.
【解答】解:菱形,长方形,平行四边形,钝角三角形中只有钝角三角形具有稳定性.
故选:D.
4.下列结论正确的是( )
A.平行四边形是轴对称图形
B.菱形的对角线互相垂直且相等
C.正方形的对称轴有4条
D.矩形的对角线互相垂直
【考点】多边形.
【分析】根据平行四边形,菱形,正方形,矩形的性质,结合选项进行判断即可.
【解答】解:A、平行四边形是中心对称图形,原说法错误,故本选项错误;
B、菱形的对角线互相垂直,但不相等,原说法错误,故本选项错误;
C、正方形既是中心对称图形又是轴对称图形,对称轴有4条,故本选项正确;
D、矩形的对角线相等,原说法错误,故本选项错误;
故选:C.
5.在平面中,下列说法正确的是( )
A.四个角相等的四边形是矩形
B.对角线垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.四边相等的四边形是正方形
【考点】多边形.
【分析】根据矩形、菱形、正方形的判定定理,即可解答.
【解答】解:A.四个角相等的四边形是矩形,正确;
B.对角线垂直的平行四边形是菱形,故错误;
C.对角线相等的平行四边形是矩形,故错误;
D.四边相等的四边形应是菱形,故错误;
故选:A.
6.当多边形的边数增加1时,它的内角和会( )
A.增加160°
B.增加180°
C.增加270°
D.增加360°
【考点】多边形内角与外角.
【分析】设原多边形边数是n,则新多边形的边数是n+1.根据多边形的内角和定理即可求得.
【解答】解:设原多边形边数是n,则n边形的内角和是(n﹣2)?180°,边数增加1,则新多边形的内角和是(n+1﹣2)?180°.
则(n+1﹣2)?180°﹣(n﹣2)?180°=180°.
故它的内角和增加180°.
故选:B.
7.已知一个多边形的外角和比它的内角和少540°,则该多边形的边数为( )
A.7
B.8
C.9
D.10
【考点】多边形内角与外角.
【分析】根据多边形的内角和公式(n﹣2)?180°,外角和等于360°列出方程求解即可.
【解答】解:设多边形的边数是n,
根据题意得,(n﹣2)?180°﹣360°=540°,
解得n=7.
故选:A.
8.下列说法中,正确的个数有( )
①同位角相等;
②三角形的高相交于三角形的内部;③三角形的一个外角大于任意一个内角;④一个多边形的边数每增加一条,这个多边形的内角和就增加180°;⑤两个角的两边分别平行,则这两个角相等.
A.0个
B.1个
C.2个
D.3个
【考点】同位角、内错角、同旁内角;三角形内角和定理;三角形的外角性质;多边形内角与外角.
【分析】根据同位角的定义、三角形内外角的关系、三角形垂心的定义及多边形内角和公式、平行线的性质逐一判断可得.
【解答】解:①只有两平行直线被第三条直线所截时,同位角才相等,故说法①错误;
②只有锐角三角形的三条高在三角形的内部,故说法②错误;
③三角形的一个外角大于任意一个和它不相邻的内角,故说法③错误;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°,此说法④正确;
⑤两个角的两边分别平行,则这两个角可能相等,也可能互补,故说法⑤错误;
正确的个数有1个,
故选:B.
9.如图,将四边形纸片ABCD沿MN折叠,若∠1+∠2=130°,则∠B+∠C=( )
A.115°
B.130°
C.135°
D.150°
【考点】多边形内角与外角.
【分析】先根据∠1+∠2=130°得出∠AMN+∠DNM的度数,再由四边形内角和定理即可得出结论.
【解答】解:∵∠1+∠2=130°,
∴∠AMN+∠DNM==115°.
∵∠A+∠D+(∠AMN+∠DNM)=360°,∠A+∠D+(∠B+∠C)=360°,
∴∠B+∠C=∠AMN+∠DNM=115°.
故选:A.
10.若一个多边形的内角和等于1800度,则这个多边形是( )
A.十二边形
B.十边形
C.九边形
D.八边形
【考点】多边形内角与外角.
【分析】根据多边形的内角和公式(n﹣2)?180°列式进行计算即可求解.
【解答】解:设多边形的边数是n,则
(n﹣2)?180=1800,
解得n=12,
所以这个多边形是十二边形.
故选:A.
二.填空题(共5小题)
11.将一个正六边形纸片对折,并完全重合,那么得到的图形是 四边形或五 边形.
【考点】多边形.
【分析】分折痕是对角线所在的直线与对边中点所在的直线两种情况讨论求解.
【解答】解:如图,①折痕是对角线所在的直线时,得到的图形是四边形,
②折痕是对边中点所在的直线时,得到的图形是五边形,
所以,得到的图形是四边形或五边形.
故答案为:四边形或五.
12.一个n边形的内角和是它外角和的6倍,则n= 14 .
【考点】多边形内角与外角.
【分析】利用多边形的内角和公式和外角和公式,根据一个n边形的内角和是其外角和的5倍列出方程求解即可.
【解答】解:多边形的外角和是360°,多边形的内角和是180°?(n﹣2),根据题意得:
180?(n﹣2)=360×6,
解得n=14.
故答案为:14.
13.已知一个多边形的每个外角都是24°,此多边形是 十五 边形.
【考点】多边形内角与外角.
【分析】任何多边形的外角和是360°.用外角和除以每个外角的度数即可得到边数.
【解答】解:360°÷24°=15.
故这个多边形是十五边形.
故答案为:十五.
14.如图,蚂蚁点P出发,沿直线行走40米后左转30°,再沿直线行走40米,又左转30°,…;照此走下去,它第一次回到出发点P,一共行走的路程是 480 米.
【考点】多边形内角与外角.
【分析】根据题意,蚂蚁走过的路程是正多边形,先用360°除以30°求出边数,然后再乘以40米即可.
【解答】解:∵蚂蚁每次都是沿直线前进40米后向左转30°,
∴它走过的图形是正多边形,
∴边数n=360°÷30°=12,
∴它第一次回到出发点P时,一共走了12×40=480(米).
故答案为:480.
15.如图,在正五边形ABCDE中,AC为对角线,以点A为圆心,AE为半径画圆弧交AC于点F,连结EF,则∠1的度数为 54° .
【考点】多边形内角与外角.
【分析】根据五边形的内角和公式求出∠ABC,根据等腰三角形的性质,三角形内角和的定理计算∠BAC,再求∠CAE,最后求出∠1即可.
【解答】解:∵五边形ABCDE是正五边形,
∴∠EAB=∠ABC==108°,
∵BA=BC,
∴∠BAC=∠BCA==36°,
∴∠EAF=108°﹣36°=72°,
∵以点A为圆心,AE为半径画圆弧交AC于点F,
∴AE=AF,
∴∠1==54°.
故答案为:54°.
三.解答题(共5小题)
16.如图1.已知大圆的直径为16米,小圆的直径比大四的直径少(注:π取3)
(1)求小圆的周长;
(2)德强学校的操场上有一个五彩的奥运五环图案,是由5个与图1完全相同的圆环构成,若每两个环形相交的部分是曲边四边形,每个曲边四边形面积都是平方米,求这个五环图形的面积.
(3)在(2)的条件下,为了迎接11月1日在我校举行的全国“70节好课致敬新中国70年”观摩课活动,学校决定重新粉剧操场上的奥运五环,学校雇佣2个师傅和4个徒弟来完成这项任务(每名师傅每小时粉刷的面积相同,每个徒弟每小时粉剧的面积相同),已知1个师傅1小时粉刷的面积是师徒6人1小时粉刷面积的.工作2小时后,4个徒弟比两个师傅多粉刷24平方米,这时两个师傅因有其它任务离开,剩下的工作由4个徒弟完成,工作完成,学校每小时支付师傅工资270元,每小时支付徒弟工资150元,学校共支付工资多少元.
【考点】认识平面图形;多边形.
【分析】(1)先计算小圆的直径,根据周长公式可得结论;
(2)理解曲边四边形是哪个图形,根据5×一个圆环的面积﹣8个曲边四边形的面积,可解答;
(3)先设1个徒弟每小时刷墙x米2,则1个师傅每小时刷墙(2x﹣6)米2,根据1个师傅1小时粉刷的面积是师徒6人1小时粉刷而积的,列方程可得师傅和徒弟的工作效率,根据已知计算徒弟工作总时间,和每小时的工资可得结论.
【解答】解:(1)由题意得:小圆的直径为:(1﹣)×16=14(米),
则小圆的周长为:π×14=3×14=42(米),
答:小圆的周长是42米;
(2)[5×﹣5×]﹣8×,
=5×3×15﹣9,
=216(米2),
答:这个五环图形的面积是216米2;
(3)设1个徒弟每小时刷墙x米2,则1个师傅每小时刷墙(2x﹣6)米2,
由题意得:2x﹣6=,
解得:x=12,
2x﹣6=2×12﹣6=18,
即设1个徒弟每小时刷墙12米2,则1个师傅每小时刷墙18米2,
=1,
即设4个徒弟干了3个小时,2个师傅干了2个小时,
3×150×4+2×270×2=2880(元),
答:学校共支付工资2880元.
17.举例说明各边相等的多边形不一定是正多边形.
【考点】多边形.
【分析】菱形的各边相等,但菱形不是正多边形.
【解答】解:各边相等的多边形不一定是正多边形,例如菱形的各边相等,但菱形不是正多边形.
18.如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别交CD、AB于点E、F,且∠1与∠2互余,∠A与∠C有怎样的数量关系?为什么?
【考点】三角形内角和定理;多边形内角与外角.
【分析】先求出∠1+∠2=90°,再求出∠ABC=2∠2,∠ADC=2∠1,即可求出∠ABC+∠ADC=2(∠1+∠2)=2×90°=180°,最后可以求出∠A+∠C=180°.
【解答】解:∠A+∠C=180°,理由如下:
∵∠1与∠2互余,
∴∠1+∠2=90°,
∵BE、DF分别平分∠ABC、∠ADC,
∴∠ABC=2∠2,∠ADC=2∠1,
∴∠ABC+∠ADC=2(∠1+∠2)=2×90°=180°,
∵∠A+∠ABC+∠C+∠ADC=360°,
∴∠A+∠C=180°.
19.【知识回顾】:
如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD= ∠A+∠B .
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB= 80 °.(直接写出答案)
(2)若∠A=70°,则∠DBC+∠ECB= 250 °.(直接写出答案)
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP= 220 °.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
【考点】平行线的判定;三角形内角和定理;三角形的外角性质;多边形内角与外角.
【分析】【知识回顾】
根据三角形的内角和定理和平角的定义可得结论;
【初步运用】
(1)根据三角形的外角等于与它不相邻的两个内角的和列式可得结论;
(2)根据三角形的内角和得:∠ABC+∠ACB=110°,由两个平角的和可得结论;
【拓展延伸】
(1)连接AP,根据三角形内角和定理的推论可得等式,将两个等式相加可得结论;
(2)如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,综合可得结论;
(3)如图⑥,作辅助线,构建三角形PQC,根据(1)的结论得:∠DBP+∠ECP=∠A+∠BPC,和角平分线的定义,证明∠MBP=∠PQC,可得结论.
【解答】解:【知识回顾】
∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠B;
故答案为:∠A+∠B;
【初步运用】
(1)∵∠DBC=∠A+∠ACB,∠A=70°,∠DBC=150°,
∴∠ACB=∠DBC﹣∠A=150°﹣70°=80°;
故答案为:80;
(2)∵∠A=70°,
∴∠ABC+∠ACB=110°,
∴∠DBC+∠ECB=360°﹣110°=250°,
故答案为:250;
【拓展延伸】
(1)如图④,连接AP,∵∠DBP=∠BAP+∠APB,∠ECP=∠CAP+∠APC,
∴∠DBP+∠ECP=∠BAP+∠APB+∠CAP+∠APC=∠BAC+∠BPC,
∵∠BAC=70°,∠BPC=150°,
∴∠DBP+∠ECP=∠BAC+∠BPC=70°+150°=220°,
故答案为:220;
(2)∠A和∠P之间的数量关系是:∠P=∠A+80°,
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=40°,
∴∠P=∠A+80°;
(3)证明:如图,延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN.
20.已知:在四边形ABCD中,∠A=∠C=90°.
(1)如图1,求∠B与∠D的和为多少度?
(2)如图2,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F,求证:BE∥DF.
【考点】平行线的判定;三角形内角和定理;多边形内角与外角.
【分析】(1)根据四边形内角和定理得出∠B+∠D=180°;
(2)首先根据四边形内角和定理得出∠ABC+∠ADC=180°,进而利用角平分线的性质得出∠ABE+∠EDF=90°,即可得出∠AEB=∠ADF,利用平行线的判定得出即可.
【解答】(1)解:∵∠A=∠C=90°,
∴∠B+∠D+∠A+∠C=(4﹣2)×180°=360°,
∴∠B+∠D=360°﹣∠A﹣∠C=180°;
即∠B与∠D的和为180度;
(2)证明:∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°﹣∠A﹣∠C=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE+∠EDF=90°,
∵∠ABE+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
