2020-2021学年人教新版八年级数学上册《12.3 角的平分线的性质》高频易错题汇编(附解析)
文档属性
| 名称 | 2020-2021学年人教新版八年级数学上册《12.3 角的平分线的性质》高频易错题汇编(附解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 440.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
12.3
角的平分线的性质
高频易错题汇编
一.选择题(共10小题)
1.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15
B.30
C.45
D.60
2.如图,在四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )
A.1
B.6
C.3
D.12
3.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,若CD=4,则点D到AB的距离是( )
A.4
B.3
C.2
D.5
4.如图,直线l1,l2,l3表示三条相交叉的公路.现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地点有( )
A.四处
B.三处
C.两处
D.一处
5.点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )
A.PQ≤5
B.PQ<5
C.PQ≥5
D.PQ>5
6.点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离是( )
A.1
B.2
C.3
D.4
7.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,BE=2,BC=6,则△BDE的周长为( )
A.6
B.8
C.10
D.14
8.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
A.①
B.②
C.①②
D.①②③
9.如图,Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,AB=10,则△ABD的面积等于( )
A.30
B.24
C.15
D.10
10.在下列各题中,属于尺规作图的是( )
A.利用三角板画45°的角
B.用直尺和三角板画平行线
C.用直尺画一工件边缘的垂线
D.用圆规在已知直线上截取一条线段等于已知线段
二.填空题(共5小题)
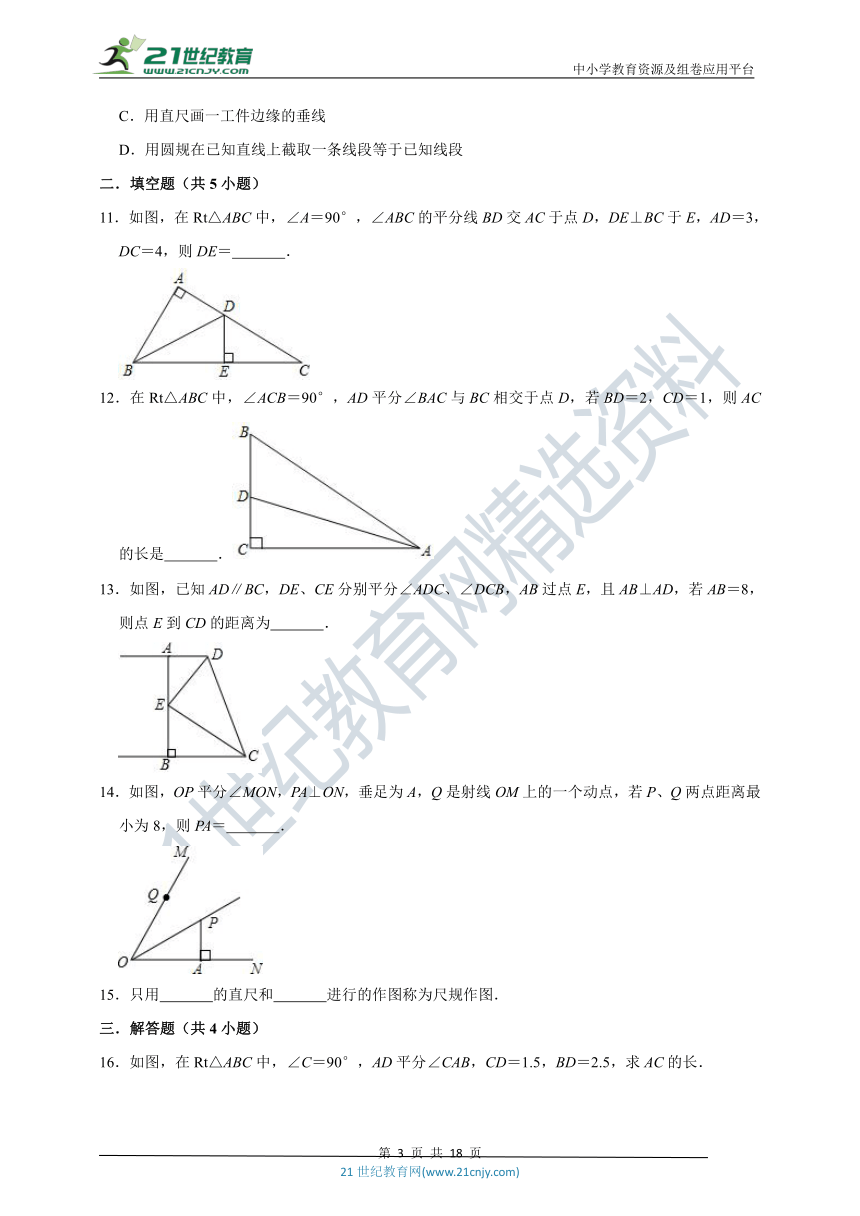
11.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,DE⊥BC于E,AD=3,DC=4,则DE=
.
12.在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=2,CD=1,则AC的长是
.
13.如图,已知AD∥BC,DE、CE分别平分∠ADC、∠DCB,AB过点E,且AB⊥AD,若AB=8,则点E到CD的距离为
.
14.如图,OP平分∠MON,PA⊥ON,垂足为A,Q是射线OM上的一个动点,若P、Q两点距离最小为8,则PA=
.
15.只用
的直尺和
进行的作图称为尺规作图.
三.解答题(共4小题)
16.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=1.5,BD=2.5,求AC的长.
17.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
18.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE,
求证:FK∥AB.
19.求证:角平分线上的点到这个角的两边距离相等.
已知:
求证:
证明:
试题解析
一.选择题(共10小题)
1.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15
B.30
C.45
D.60
【考点】角平分线的性质.
【分析】作DE⊥AB于E,根据角平分线的性质得到DE=DC=4,根据三角形的面积公式计算即可.
【解答】解:作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=4,
∴△ABD的面积=×AB×DE=30,
故选:B.
2.如图,在四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )
A.1
B.6
C.3
D.12
【考点】角平分线的性质.
【分析】由三角形的内角和定理和角的和差求出∠ABD=∠CBD,角平分线的性质定理得AD=DH,垂线段定义证明DH最短,求出DP长的最小值为3.
【解答】解:过点D作DH⊥BC交BC于点H,如图所示:
∵BD⊥CD,
∴∠BDC=90°,
又∵∠C+∠BDC+∠DBC=180°,
∠ADB+∠A+∠ABD=180°
∠ADB=∠C,∠A=90°,
∴∠ABD=∠CBD,
∴BD是∠ABC的角平分线,
又∵AD⊥AB,DH⊥BC,
∴AD=DH,
又∵AD=3,
∴DH=3,
又∴点D是直线BC外一点,
∴当点P在BC上运动时,点P运动到与点H重合时DP最短,其长度为DH长等于3,
即DP长的最小值为3.
故选:C.
3.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,若CD=4,则点D到AB的距离是( )
A.4
B.3
C.2
D.5
【考点】角平分线的性质.
【分析】作DH⊥AB于H.根据角平分线的性质定理得出CD=DH,代入求出即可.
【解答】解:如图,作DH⊥AB于H.
∵∠C=90°,AD平分∠BAC交BC于点D,
∴CD=DH(角的平分线上的点到角的两边的距离相等),
∵CD=4,
∴DH=4,即点D到AB的距离是4.
故选:A.
4.如图,直线l1,l2,l3表示三条相交叉的公路.现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地点有( )
A.四处
B.三处
C.两处
D.一处
【考点】角平分线的性质.
【分析】由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
【解答】解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三角形外角平分线的交点,共三处.
故选:A.
5.点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )
A.PQ≤5
B.PQ<5
C.PQ≥5
D.PQ>5
【考点】角平分线的性质.
【分析】根据角平分线上的点到角的两边距离相等可得点P到OB的距离为5,再根据垂线段最短解答.
【解答】解:∵点P在∠AOB的平分线上,点P到OA边的距离等于5,
∴点P到OB的距离为5,
∵点Q是OB边上的任意一点,
∴PQ≥5.
故选:C.
6.点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离是( )
A.1
B.2
C.3
D.4
【考点】角平分线的性质.
【分析】过O作OE⊥AB,OF⊥AC,连接AO,依据△ABC的面积是12,周长是8,即可得出点O到边BC的距离.
【解答】解:如图所示,过O作OE⊥AB,OF⊥AC,连接AO,
∵点O是△ABC中∠BCA,∠ABC的平分线的交点,
∴OE=OD=OF,
∵△ABC的面积是12,周长是8,
∴AB×OE+BC×OD+AC×OF=12,
即×8×OD=12,
即OD=3,
故选:C.
7.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,BE=2,BC=6,则△BDE的周长为( )
A.6
B.8
C.10
D.14
【考点】角平分线的性质.
【分析】根据角平分线的性质得到CD=DE,根据三角形的周长公式计算即可.
【解答】解:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴CD=DE,
∴△BDE的周长=BD+DE+BE=BD+CD+BE=BC+BE=8,
故选:B.
8.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
A.①
B.②
C.①②
D.①②③
【考点】全等三角形的判定;角平分线的性质.
【分析】从已知条件进行分析,首先可得△ABE≌△ACF得到角相等,边相等,运用这些结论,进而得到更多的结论,最好运用排除法对各个选项进行验证从而确定最终答案.
【解答】解:∵BE⊥AC于E,CF⊥AB于F
∴∠AEB=∠AFC=90°,
∵AB=AC,∠A=∠A,
∴△ABE≌△ACF(第一个正确)
∴AE=AF,
∴BF=CE,
∵BE⊥AC于E,CF⊥AB于F,∠BDF=∠CDE,
∴△BDF≌△CDE(第二个正确)
∴DF=DE,
连接AD
∵AE=AF,DE=DF,AD=AD,
∴△AED≌△AFD,
∴∠FAD=∠EAD,
即点D在∠BAC的平分线上(第三个正确)
故选:D.
9.如图,Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,AB=10,则△ABD的面积等于( )
A.30
B.24
C.15
D.10
【考点】角平分线的性质.
【分析】过D作DE⊥AB于E,由角平分线的性质,即可求得DE的长,继而求得三角形面积.
【解答】解:如图,过D作DE⊥AB于E,
∵AD平分∠BAC,∠C=90°,
∴DE=DC=3,
∵AB=10,
∴△ABD的面积=AB?DE=×10×3=15.
故选:C.
10.在下列各题中,属于尺规作图的是( )
A.利用三角板画45°的角
B.用直尺和三角板画平行线
C.用直尺画一工件边缘的垂线
D.用圆规在已知直线上截取一条线段等于已知线段
【考点】作图—尺规作图的定义.
【分析】尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
【解答】解:A、利用三角板画45°的角不符合尺规作图的定义,错误;
B、用直尺和三角板画平行线不符合尺规作图的定义,错误;
C、用直尺画一工件边缘的垂线不符合尺规作图的定义,错误;
D、用圆规在已知直线上截取一条线段等于已知线段符合尺规作图的定义,正确.
故选:D.
二.填空题(共5小题)
11.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,DE⊥BC于E,AD=3,DC=4,则DE= 3 .
【考点】角平分线的性质.
【分析】根据角平分线的性质得到DE=AD=3.
【解答】解:∵∠A=90°,
∴DA⊥BA,
又∵BD是∠ABC的平分线,DE⊥BC,
∴DE=AD,
∵AD=3,
∴DE=3,
故答案为:3.
12.在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=2,CD=1,则AC的长是 .
【考点】角平分线的性质.
【分析】作DE⊥AB于E,根据角平分线的性质得到DE=DC,根据勾股定理求出BE,再根据勾股定理计算即可.
【解答】解:作DE⊥AB于E,
∵AD是∠BAC的平分线,∠ACB=90°,DE⊥AB,
∴DE=DC=1,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
由勾股定理得BE===,
设AC=AE=x,
由勾股定理得x2+32=(x+)2,
解得x=.
∴AC=.
故答案为:.
13.如图,已知AD∥BC,DE、CE分别平分∠ADC、∠DCB,AB过点E,且AB⊥AD,若AB=8,则点E到CD的距离为 4 .
【考点】平行线的性质;角平分线的性质.
【分析】过点E作EF⊥CD于F,根据两直线平行,同旁内角互补可得∠B=90°,然后根据角平分线上的点到角的两边距离相等可得AE=EF=BE,从而得解.
【解答】解:如图,过点E作EF⊥CD于F,
∵AD∥BC,AB⊥AD,
∴∠A=∠B=180°﹣90°=90°,
∵CE平分∠BCD,DE平分∠ADC,
∴AE=EF=BE,
∵AB=8,
∴EF=×8=4,
即点E到CD的距离为4.
故答案为:4.
14.如图,OP平分∠MON,PA⊥ON,垂足为A,Q是射线OM上的一个动点,若P、Q两点距离最小为8,则PA= 8 .
【考点】角平分线的性质.
【分析】根据题意点Q是射线OM上的一个动点,要求PQ的最小值,需要找出满足题意的点Q,根据直线外一点与直线上各点连接的所有线段中,垂线段最短,所以过点P作PQ垂直OM,此时的PQ最短,然后根据角平分线上的点到角两边的距离相等可得PA=PQ.
【解答】解:过点P作PQ⊥OM,垂足为Q,则PQ长为P、Q两点最短距离,
∵OP平分∠MON,PA⊥ON,PQ⊥OM,
∴PA=PQ=8,
故答案为:8.
15.只用 没有刻度的 的直尺和 圆规 进行的作图称为尺规作图.
【考点】作图—尺规作图的定义.
【分析】尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
【解答】解:只用没有刻度的直尺和圆规进行的作图称为尺规作图.
故答案为:没有刻度的,圆规.
三.解答题(共4小题)
16.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=1.5,BD=2.5,求AC的长.
【考点】角平分线的性质.
【分析】过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得CD=DE,再利用勾股定理列式求出BE,然后设AC=AE=x,根据勾股定理列式计算即可得解.
【解答】解:如图,过D作DE⊥AB于E,
∵∠C=90°,AD平分∠CAB,CD=1.5,
∴DE=CD=1.5,
在Rt△DEB中,由勾股定理得:
BE===2,
∵AD=AD,CD=DE,∠C=∠AED,
∴Rt△ACD≌Rt△AED,
∴AC=AE,
设AC=AE=x,则AB=x+2,
由勾股定理得:AB2=AC2+CB2,
即(x+2)2=x2+42,
解得x=3,
∴AC=3.
17.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
【考点】全等三角形的判定与性质;角平分线的性质.
【分析】(1)根据角平分线性质可证ED=EC,从而可知△CDE为等腰三角形,可证∠ECD=∠EDC;
(2)由OE平分∠AOB,EC⊥OA,ED⊥OB,OE=OE,可证△OED≌△OEC,可得OC=OD;
(3)根据ED=EC,OC=OD,可证OE是线段CD的垂直平分线.
【解答】证明:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴ED=EC,即△CDE为等腰三角形,
∴∠ECD=∠EDC;
(2)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴∠DOE=∠COE,∠ODE=∠OCE=90°,OE=OE,
∴△OED≌△OEC(AAS),
∴OC=OD;
(3)∵OC=OD,且DE=EC,
∴OE是线段CD的垂直平分线.
18.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE,
求证:FK∥AB.
【考点】平行线的判定;全等三角形的判定与性质;角平分线的性质.
【分析】过点K作MK∥BC,根据AE是∠BAC的平分线及∠ACB=90°,CD⊥AB可求出∠DKA=∠CEA,再由对顶角的性质知∠DKA=∠CKE,故CK=BF,由MK∥BC可知∠B=∠AMK,∠AMK=∠DCA,由全等三角形的判定定理可知△AMK≌△ACK,根据全等三角形的性质可知,CK=MK,MK=BF,MK∥BF,故四边形BFKM是平行四边形,所以FK∥AB.
【解答】证明:过点K作MK∥BC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
又∵∠ACB=90°,CD⊥AB,
∴∠BAE+∠DKA=∠CAE+∠CEA=90°,
∴∠DKA=∠CEA,
又∵∠DKA=∠CKE,
∴∠CEA=∠CKE,∴CE=CK,又CE=BF,
∴CK=BF(4分)
而MK∥BC,
∴∠B=∠AMK,
∴∠BCD+∠B=∠DCA+∠BCD=90°,
∴∠AMK=∠DCA,
在△AMK和△ACK中,
∴∠AMK=∠ACK,AK=AK,∠MAK=∠CAK,
∴△AMK≌△ACK,(4分)
∴CK=MK,
∴MK=BF,MK∥BF,
四边形BFKM是平行四边形,(2分)
∴FK∥AB.(2分)
19.求证:角平分线上的点到这个角的两边距离相等.
已知:
求证:
证明:
【考点】全等三角形的判定与性质;角平分线的性质.
【分析】结合已知条件,根据全等三角形的判定和性质,推出△POE≌△POF即可.
【解答】已知:如图,OC是∠AOB的平分线,P是OC上任意一点,PE⊥OA,PF⊥OB,垂足分别为E、F,(2分)
求证:PE=PF(3分)
证明:∵OC是∠AOB的平分线,
∴∠POE=∠POF,(4分)
∵PE⊥OA,PF⊥OB,
∴∠PEO=∠PFO,(5分)
又∵OP=OP,(6分)
∴△POE≌△POF,(7分)
∴PE=PF.(8分)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.3
角的平分线的性质
高频易错题汇编
一.选择题(共10小题)
1.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15
B.30
C.45
D.60
2.如图,在四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )
A.1
B.6
C.3
D.12
3.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,若CD=4,则点D到AB的距离是( )
A.4
B.3
C.2
D.5
4.如图,直线l1,l2,l3表示三条相交叉的公路.现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地点有( )
A.四处
B.三处
C.两处
D.一处
5.点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )
A.PQ≤5
B.PQ<5
C.PQ≥5
D.PQ>5
6.点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离是( )
A.1
B.2
C.3
D.4
7.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,BE=2,BC=6,则△BDE的周长为( )
A.6
B.8
C.10
D.14
8.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
A.①
B.②
C.①②
D.①②③
9.如图,Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,AB=10,则△ABD的面积等于( )
A.30
B.24
C.15
D.10
10.在下列各题中,属于尺规作图的是( )
A.利用三角板画45°的角
B.用直尺和三角板画平行线
C.用直尺画一工件边缘的垂线
D.用圆规在已知直线上截取一条线段等于已知线段
二.填空题(共5小题)
11.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,DE⊥BC于E,AD=3,DC=4,则DE=
.
12.在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=2,CD=1,则AC的长是
.
13.如图,已知AD∥BC,DE、CE分别平分∠ADC、∠DCB,AB过点E,且AB⊥AD,若AB=8,则点E到CD的距离为
.
14.如图,OP平分∠MON,PA⊥ON,垂足为A,Q是射线OM上的一个动点,若P、Q两点距离最小为8,则PA=
.
15.只用
的直尺和
进行的作图称为尺规作图.
三.解答题(共4小题)
16.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=1.5,BD=2.5,求AC的长.
17.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
18.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE,
求证:FK∥AB.
19.求证:角平分线上的点到这个角的两边距离相等.
已知:
求证:
证明:
试题解析
一.选择题(共10小题)
1.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15
B.30
C.45
D.60
【考点】角平分线的性质.
【分析】作DE⊥AB于E,根据角平分线的性质得到DE=DC=4,根据三角形的面积公式计算即可.
【解答】解:作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=4,
∴△ABD的面积=×AB×DE=30,
故选:B.
2.如图,在四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )
A.1
B.6
C.3
D.12
【考点】角平分线的性质.
【分析】由三角形的内角和定理和角的和差求出∠ABD=∠CBD,角平分线的性质定理得AD=DH,垂线段定义证明DH最短,求出DP长的最小值为3.
【解答】解:过点D作DH⊥BC交BC于点H,如图所示:
∵BD⊥CD,
∴∠BDC=90°,
又∵∠C+∠BDC+∠DBC=180°,
∠ADB+∠A+∠ABD=180°
∠ADB=∠C,∠A=90°,
∴∠ABD=∠CBD,
∴BD是∠ABC的角平分线,
又∵AD⊥AB,DH⊥BC,
∴AD=DH,
又∵AD=3,
∴DH=3,
又∴点D是直线BC外一点,
∴当点P在BC上运动时,点P运动到与点H重合时DP最短,其长度为DH长等于3,
即DP长的最小值为3.
故选:C.
3.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,若CD=4,则点D到AB的距离是( )
A.4
B.3
C.2
D.5
【考点】角平分线的性质.
【分析】作DH⊥AB于H.根据角平分线的性质定理得出CD=DH,代入求出即可.
【解答】解:如图,作DH⊥AB于H.
∵∠C=90°,AD平分∠BAC交BC于点D,
∴CD=DH(角的平分线上的点到角的两边的距离相等),
∵CD=4,
∴DH=4,即点D到AB的距离是4.
故选:A.
4.如图,直线l1,l2,l3表示三条相交叉的公路.现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地点有( )
A.四处
B.三处
C.两处
D.一处
【考点】角平分线的性质.
【分析】由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
【解答】解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三角形外角平分线的交点,共三处.
故选:A.
5.点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )
A.PQ≤5
B.PQ<5
C.PQ≥5
D.PQ>5
【考点】角平分线的性质.
【分析】根据角平分线上的点到角的两边距离相等可得点P到OB的距离为5,再根据垂线段最短解答.
【解答】解:∵点P在∠AOB的平分线上,点P到OA边的距离等于5,
∴点P到OB的距离为5,
∵点Q是OB边上的任意一点,
∴PQ≥5.
故选:C.
6.点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离是( )
A.1
B.2
C.3
D.4
【考点】角平分线的性质.
【分析】过O作OE⊥AB,OF⊥AC,连接AO,依据△ABC的面积是12,周长是8,即可得出点O到边BC的距离.
【解答】解:如图所示,过O作OE⊥AB,OF⊥AC,连接AO,
∵点O是△ABC中∠BCA,∠ABC的平分线的交点,
∴OE=OD=OF,
∵△ABC的面积是12,周长是8,
∴AB×OE+BC×OD+AC×OF=12,
即×8×OD=12,
即OD=3,
故选:C.
7.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,BE=2,BC=6,则△BDE的周长为( )
A.6
B.8
C.10
D.14
【考点】角平分线的性质.
【分析】根据角平分线的性质得到CD=DE,根据三角形的周长公式计算即可.
【解答】解:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴CD=DE,
∴△BDE的周长=BD+DE+BE=BD+CD+BE=BC+BE=8,
故选:B.
8.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
A.①
B.②
C.①②
D.①②③
【考点】全等三角形的判定;角平分线的性质.
【分析】从已知条件进行分析,首先可得△ABE≌△ACF得到角相等,边相等,运用这些结论,进而得到更多的结论,最好运用排除法对各个选项进行验证从而确定最终答案.
【解答】解:∵BE⊥AC于E,CF⊥AB于F
∴∠AEB=∠AFC=90°,
∵AB=AC,∠A=∠A,
∴△ABE≌△ACF(第一个正确)
∴AE=AF,
∴BF=CE,
∵BE⊥AC于E,CF⊥AB于F,∠BDF=∠CDE,
∴△BDF≌△CDE(第二个正确)
∴DF=DE,
连接AD
∵AE=AF,DE=DF,AD=AD,
∴△AED≌△AFD,
∴∠FAD=∠EAD,
即点D在∠BAC的平分线上(第三个正确)
故选:D.
9.如图,Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,AB=10,则△ABD的面积等于( )
A.30
B.24
C.15
D.10
【考点】角平分线的性质.
【分析】过D作DE⊥AB于E,由角平分线的性质,即可求得DE的长,继而求得三角形面积.
【解答】解:如图,过D作DE⊥AB于E,
∵AD平分∠BAC,∠C=90°,
∴DE=DC=3,
∵AB=10,
∴△ABD的面积=AB?DE=×10×3=15.
故选:C.
10.在下列各题中,属于尺规作图的是( )
A.利用三角板画45°的角
B.用直尺和三角板画平行线
C.用直尺画一工件边缘的垂线
D.用圆规在已知直线上截取一条线段等于已知线段
【考点】作图—尺规作图的定义.
【分析】尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
【解答】解:A、利用三角板画45°的角不符合尺规作图的定义,错误;
B、用直尺和三角板画平行线不符合尺规作图的定义,错误;
C、用直尺画一工件边缘的垂线不符合尺规作图的定义,错误;
D、用圆规在已知直线上截取一条线段等于已知线段符合尺规作图的定义,正确.
故选:D.
二.填空题(共5小题)
11.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,DE⊥BC于E,AD=3,DC=4,则DE= 3 .
【考点】角平分线的性质.
【分析】根据角平分线的性质得到DE=AD=3.
【解答】解:∵∠A=90°,
∴DA⊥BA,
又∵BD是∠ABC的平分线,DE⊥BC,
∴DE=AD,
∵AD=3,
∴DE=3,
故答案为:3.
12.在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=2,CD=1,则AC的长是 .
【考点】角平分线的性质.
【分析】作DE⊥AB于E,根据角平分线的性质得到DE=DC,根据勾股定理求出BE,再根据勾股定理计算即可.
【解答】解:作DE⊥AB于E,
∵AD是∠BAC的平分线,∠ACB=90°,DE⊥AB,
∴DE=DC=1,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
由勾股定理得BE===,
设AC=AE=x,
由勾股定理得x2+32=(x+)2,
解得x=.
∴AC=.
故答案为:.
13.如图,已知AD∥BC,DE、CE分别平分∠ADC、∠DCB,AB过点E,且AB⊥AD,若AB=8,则点E到CD的距离为 4 .
【考点】平行线的性质;角平分线的性质.
【分析】过点E作EF⊥CD于F,根据两直线平行,同旁内角互补可得∠B=90°,然后根据角平分线上的点到角的两边距离相等可得AE=EF=BE,从而得解.
【解答】解:如图,过点E作EF⊥CD于F,
∵AD∥BC,AB⊥AD,
∴∠A=∠B=180°﹣90°=90°,
∵CE平分∠BCD,DE平分∠ADC,
∴AE=EF=BE,
∵AB=8,
∴EF=×8=4,
即点E到CD的距离为4.
故答案为:4.
14.如图,OP平分∠MON,PA⊥ON,垂足为A,Q是射线OM上的一个动点,若P、Q两点距离最小为8,则PA= 8 .
【考点】角平分线的性质.
【分析】根据题意点Q是射线OM上的一个动点,要求PQ的最小值,需要找出满足题意的点Q,根据直线外一点与直线上各点连接的所有线段中,垂线段最短,所以过点P作PQ垂直OM,此时的PQ最短,然后根据角平分线上的点到角两边的距离相等可得PA=PQ.
【解答】解:过点P作PQ⊥OM,垂足为Q,则PQ长为P、Q两点最短距离,
∵OP平分∠MON,PA⊥ON,PQ⊥OM,
∴PA=PQ=8,
故答案为:8.
15.只用 没有刻度的 的直尺和 圆规 进行的作图称为尺规作图.
【考点】作图—尺规作图的定义.
【分析】尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
【解答】解:只用没有刻度的直尺和圆规进行的作图称为尺规作图.
故答案为:没有刻度的,圆规.
三.解答题(共4小题)
16.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=1.5,BD=2.5,求AC的长.
【考点】角平分线的性质.
【分析】过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得CD=DE,再利用勾股定理列式求出BE,然后设AC=AE=x,根据勾股定理列式计算即可得解.
【解答】解:如图,过D作DE⊥AB于E,
∵∠C=90°,AD平分∠CAB,CD=1.5,
∴DE=CD=1.5,
在Rt△DEB中,由勾股定理得:
BE===2,
∵AD=AD,CD=DE,∠C=∠AED,
∴Rt△ACD≌Rt△AED,
∴AC=AE,
设AC=AE=x,则AB=x+2,
由勾股定理得:AB2=AC2+CB2,
即(x+2)2=x2+42,
解得x=3,
∴AC=3.
17.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
【考点】全等三角形的判定与性质;角平分线的性质.
【分析】(1)根据角平分线性质可证ED=EC,从而可知△CDE为等腰三角形,可证∠ECD=∠EDC;
(2)由OE平分∠AOB,EC⊥OA,ED⊥OB,OE=OE,可证△OED≌△OEC,可得OC=OD;
(3)根据ED=EC,OC=OD,可证OE是线段CD的垂直平分线.
【解答】证明:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴ED=EC,即△CDE为等腰三角形,
∴∠ECD=∠EDC;
(2)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴∠DOE=∠COE,∠ODE=∠OCE=90°,OE=OE,
∴△OED≌△OEC(AAS),
∴OC=OD;
(3)∵OC=OD,且DE=EC,
∴OE是线段CD的垂直平分线.
18.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE,
求证:FK∥AB.
【考点】平行线的判定;全等三角形的判定与性质;角平分线的性质.
【分析】过点K作MK∥BC,根据AE是∠BAC的平分线及∠ACB=90°,CD⊥AB可求出∠DKA=∠CEA,再由对顶角的性质知∠DKA=∠CKE,故CK=BF,由MK∥BC可知∠B=∠AMK,∠AMK=∠DCA,由全等三角形的判定定理可知△AMK≌△ACK,根据全等三角形的性质可知,CK=MK,MK=BF,MK∥BF,故四边形BFKM是平行四边形,所以FK∥AB.
【解答】证明:过点K作MK∥BC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
又∵∠ACB=90°,CD⊥AB,
∴∠BAE+∠DKA=∠CAE+∠CEA=90°,
∴∠DKA=∠CEA,
又∵∠DKA=∠CKE,
∴∠CEA=∠CKE,∴CE=CK,又CE=BF,
∴CK=BF(4分)
而MK∥BC,
∴∠B=∠AMK,
∴∠BCD+∠B=∠DCA+∠BCD=90°,
∴∠AMK=∠DCA,
在△AMK和△ACK中,
∴∠AMK=∠ACK,AK=AK,∠MAK=∠CAK,
∴△AMK≌△ACK,(4分)
∴CK=MK,
∴MK=BF,MK∥BF,
四边形BFKM是平行四边形,(2分)
∴FK∥AB.(2分)
19.求证:角平分线上的点到这个角的两边距离相等.
已知:
求证:
证明:
【考点】全等三角形的判定与性质;角平分线的性质.
【分析】结合已知条件,根据全等三角形的判定和性质,推出△POE≌△POF即可.
【解答】已知:如图,OC是∠AOB的平分线,P是OC上任意一点,PE⊥OA,PF⊥OB,垂足分别为E、F,(2分)
求证:PE=PF(3分)
证明:∵OC是∠AOB的平分线,
∴∠POE=∠POF,(4分)
∵PE⊥OA,PF⊥OB,
∴∠PEO=∠PFO,(5分)
又∵OP=OP,(6分)
∴△POE≌△POF,(7分)
∴PE=PF.(8分)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
