2020-2021学年人教新版八年级数学上册《13.1 轴对称》高频易错题汇编(附解析)
文档属性
| 名称 | 2020-2021学年人教新版八年级数学上册《13.1 轴对称》高频易错题汇编(附解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 544.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
13.1
轴对称
高频易错题汇编
一.选择题(共10小题)
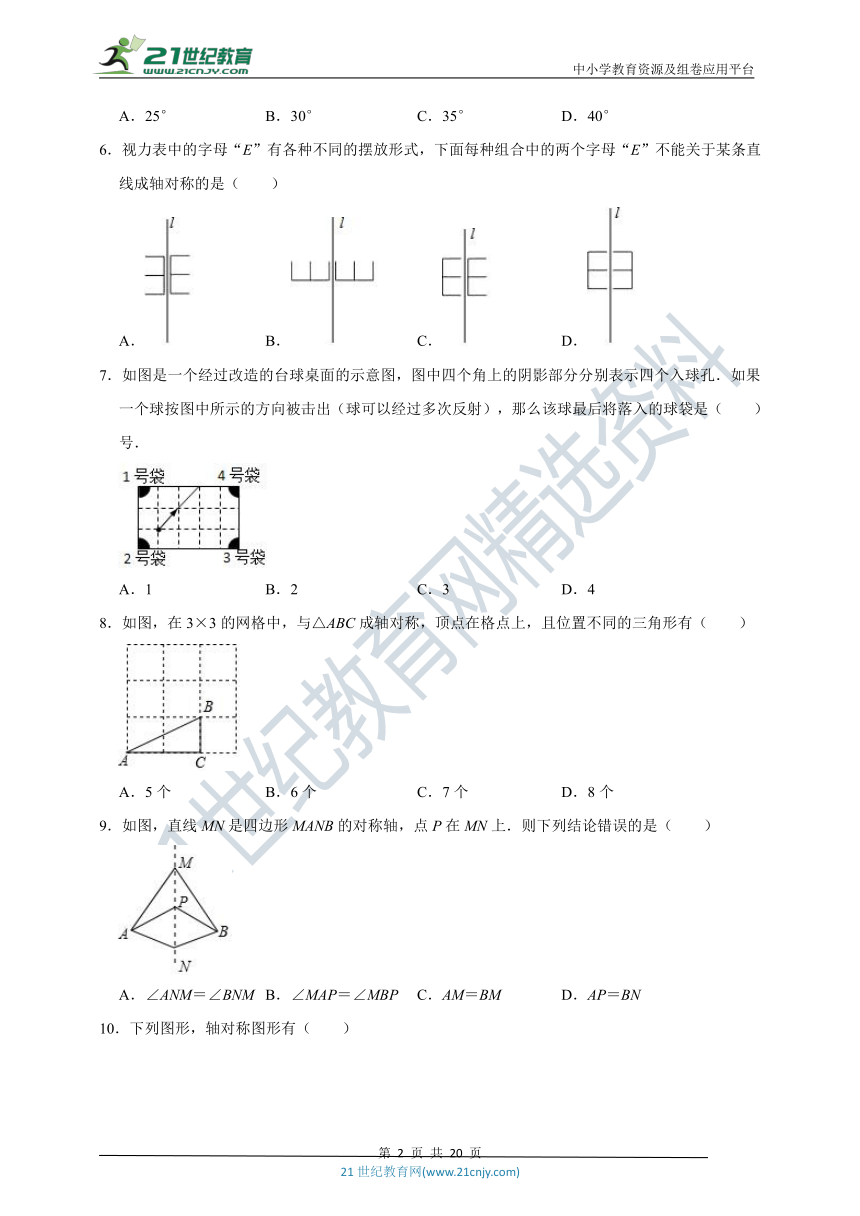
1.如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于点D.若AD=5,CD=3,则BC长是( )
A.7
B.8
C.12
D.13
2.如图,在△ABC中,DE垂直平分AC,若BC=22cm,AB=14cm,则△ABD的周长为( )
A.24cm
B.25cm
C.30cm
D.36cm
3.如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数( )
A.40°
B.70°
C.30°
D.50°
4.如图,在△ABC中,∠A=90°,∠C=30°,PQ垂直平分BC,与AC交于点P,下列结论正确的是( )
A.PC<2PA
B.PC>2PA
C.AB<2PA
D.AB>2PA
5.已知锐角三角形ABC中,∠A=65°,点O是AB、AC垂直平分线的交点,则∠BCO的度数是( )
A.25°
B.30°
C.35°
D.40°
6.视力表中的字母“E”有各种不同的摆放形式,下面每种组合中的两个字母“E”不能关于某条直线成轴对称的是( )
A.
B.
C.
D.
7.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1
B.2
C.3
D.4
8.如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( )
A.5个
B.6个
C.7个
D.8个
9.如图,直线MN是四边形MANB的对称轴,点P在MN上.则下列结论错误的是( )
A.∠ANM=∠BNM
B.∠MAP=∠MBP
C.AM=BM
D.AP=BN
10.下列图形,轴对称图形有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共5小题)
11.如图,在△ABC中,∠B=40°,∠C=45°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,则∠DAE=
.
12.△ABC中,DF是AB的垂直平分线,交BC于D,EG是AC的垂直平分线,交BC于E,若∠DAE=30°,则∠BAC等于
.
13.如图,DE是△ABC边AC的垂直平分线,若BC=8,AD=3,则BD=
.
14.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,在格纸中能画出与△ABC成轴对称且也以格点为顶点的三角形(不包括△ABC本身),这样的三角形共有
个
15.如图,在正方形ABCD中,有面积为4的正方形EFGH和面积为2的正方形PQMN,点E、F、P、Q分别在边AB、BC、CD、AD上,点M、N在边HG上,且组成的图形为轴对称图形,则正方形ABCD的面积为
.
三.解答题(共5小题)
16.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB,BC于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
17.如图,在△ABC中,∠C=90°,DE为AB的垂直平分线,DE交AC于点D,连接BD.若∠ABD=2∠CBD,求∠A的度数.
18.已知:如图,AF平分∠BAC,BC垂直平分AD,垂足为E,CF上一点P,连结PB交线段AF相交于点M.
(1)求证:AB∥CD;
(2)若∠DAC=∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
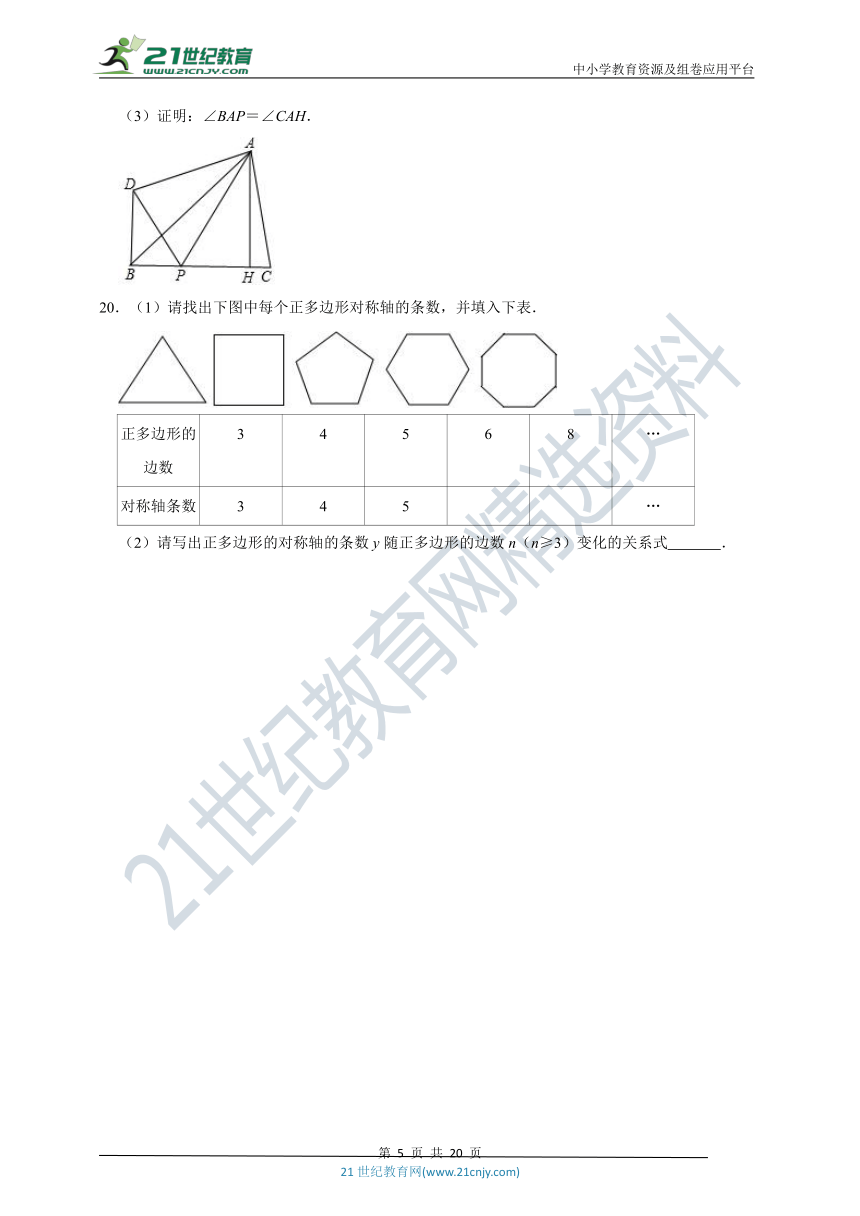
19.如图,在△ABC中,∠ABC=45°,点P为边BC上的一点,BC=3BP,且∠PAB=15°点C关于直线PA的对称点为D,连接BD,又△APC的PC边上的高为AH
(1)求∠BPD的大小;
(2)判断直线BD,AH是否平行?并说明理由;
(3)证明:∠BAP=∠CAH.
20.(1)请找出下图中每个正多边形对称轴的条数,并填入下表.
正多边形的边数
3
4
5
6
8
…
对称轴条数
3
4
5
…
(2)请写出正多边形的对称轴的条数y随正多边形的边数n(n≥3)变化的关系式
.
试题解析
一.选择题(共10小题)
1.如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于点D.若AD=5,CD=3,则BC长是( )
A.7
B.8
C.12
D.13
【考点】线段垂直平分线的性质.
【分析】由尺规作图可知,MN是线段AB的垂直平分线,即可得出DA=DB=5,依据CD的长即可得到BC=CD+BD=8.
【解答】解:由尺规作图可知,MN是线段AB的垂直平分线,
∴DA=DB=5,
又∵CD=3,
∴BC=CD+BD=3+5=8,
故选:B.
2.如图,在△ABC中,DE垂直平分AC,若BC=22cm,AB=14cm,则△ABD的周长为( )
A.24cm
B.25cm
C.30cm
D.36cm
【考点】线段垂直平分线的性质.
【分析】根据线段的垂直平分线的性质得到DA=DC,根据三角形的周长公式计算即可.
【解答】解:∵DE垂直平分AC,
∴DA=DC,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=36(cm).
故选:D.
3.如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数( )
A.40°
B.70°
C.30°
D.50°
【考点】线段垂直平分线的性质.
【分析】根据等腰三角形的性质、三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到DA=DB,得到∠DBA=∠A=40°,计算即可.
【解答】解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵MN是AB的垂直平分线,
∴DA=DB,
∴∠DBA=∠A=40°,
∴∠DBC=30°,
故选:C.
4.如图,在△ABC中,∠A=90°,∠C=30°,PQ垂直平分BC,与AC交于点P,下列结论正确的是( )
A.PC<2PA
B.PC>2PA
C.AB<2PA
D.AB>2PA
【考点】三角形三边关系;线段垂直平分线的性质.
【分析】连接BP,根据三角形内角和定理求出∠ABC=60°,根据线段垂直平分线的性质得到PB=PC,得到∠PBC=∠C=30°,根据直角三角形的性质、三角形的三边关系解答即可.
【解答】解:连接BP,
∵∠A=90°,∠C=30°,
∴∠ABC=60°,
∵PQ垂直平分BC,
∴PB=PC,
∴∠PBC=∠C=30°,
∴∠ABP=30°,
∴AP=BP=PC,
∴PC=2PA,故A、B选项错误;
∵∠A=90°,
∴AB<PB<2PA,
∴C正确,D错误;
故选:C.
5.已知锐角三角形ABC中,∠A=65°,点O是AB、AC垂直平分线的交点,则∠BCO的度数是( )
A.25°
B.30°
C.35°
D.40°
【考点】线段垂直平分线的性质.
【分析】连接OA、OB,根据三角形内角和定理求出∠ABC+∠ACB=115°,根据线段的垂直平分线的性质得到OA=OB,OA=OC,根据等腰三角形的性质计算即可.
【解答】解:如图,连接OA、OB,
∵∠BAC=65°,
∴∠ABC+∠ACB=115°,
∵O是AB,AC垂直平分线的交点,
∴OA=OB,OA=OC,
∴∠OAB=∠OBA,∠OCA=∠OAC,OB=OC,
∴∠OBA+∠OCA=65°,
∴∠OBC+∠OCB=115°﹣65°=50°,
∵OB=OC,
∴∠BCO=∠CBO=25°,
故选:A.
6.视力表中的字母“E”有各种不同的摆放形式,下面每种组合中的两个字母“E”不能关于某条直线成轴对称的是( )
A.
B.
C.
D.
【考点】生活中的轴对称现象.
【分析】把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也称轴对称,这条直线叫做对称轴.
【解答】解:A,B,D选项中,两个字母“E”关于直线l成轴对称,而C选项中,两个字母“E”不能沿着某条直线翻折互相重合.
故选:C.
7.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1
B.2
C.3
D.4
【考点】生活中的轴对称现象.
【分析】根据题意画出图形,由轴对称的性质判定正确选项.
【解答】解:根据轴对称的性质可知,台球走过的路径为:
∴该球最后将落入的球袋是4号.
故选:D.
8.如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( )
A.5个
B.6个
C.7个
D.8个
【考点】轴对称的性质.
【分析】依据对称轴的不同位置,即可得到位置不同的三角形.
【解答】解:如图所示:
与△ABC成轴对称,顶点在格点上,且位置不同的三角形有8个,
故选:D.
9.如图,直线MN是四边形MANB的对称轴,点P在MN上.则下列结论错误的是( )
A.∠ANM=∠BNM
B.∠MAP=∠MBP
C.AM=BM
D.AP=BN
【考点】轴对称的性质.
【分析】根据直线MN是四边形AMBN的对称轴,得到点A与点B对应,根据轴对称的性质即可得到结论.
【解答】解:∵直线MN是四边形AMBN的对称轴,
∴点A与点B对应,
∴AM=BM,AN=BN,∠ANM=∠BNM,
∵点P是直线MN上的点,
∴∠MAP=∠MBP,
∴A,B,C正确,而D错误,
故选:D.
10.下列图形,轴对称图形有( )
A.1个
B.2个
C.3个
D.4个
【考点】轴对称图形.
【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时也可以说这个图形关于这条直线(成轴)对称.
【解答】解:由图可得,第一个图是轴对称图形;
第二个图是轴对称图形;
第三个图是轴对称图形;
第四个图不是轴对称图形;
所以轴对称图形有3个,
故选:C.
二.填空题(共5小题)
11.如图,在△ABC中,∠B=40°,∠C=45°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,则∠DAE= 10° .
【考点】线段垂直平分线的性质.
【分析】根据线段的垂直平分线得出AD=BD,AE=CE,推出∠B=∠BAD,∠C=∠CAE,求出∠BAD+∠CAE的度数即可得到答案.
【解答】解:∵点D、E分别是AB、AC边的垂直平分线与BC的交点,
∴AD=BD,AE=CE,
∴∠B=∠BAD,∠C=∠CAE,
∵∠B=40°,∠C=45°,
∴∠B+∠C=85°,∠BAC=95°,
∴∠BAD+∠CAE=85°,
∴∠DAE=∠BAC﹣(∠BAD+∠CAE)=95°﹣85°=10°,
故答案为:10°
12.△ABC中,DF是AB的垂直平分线,交BC于D,EG是AC的垂直平分线,交BC于E,若∠DAE=30°,则∠BAC等于 75°或105° .
【考点】三角形内角和定理;线段垂直平分线的性质.
【分析】分两种情况讨论:∠BAC为锐角,∠BAC为钝角.先根据线段垂直平分线的性质,得出DA=DB,EC=EA,得到∠B=∠BAD,∠C=∠CAE,再根据关系式∠DAE=∠BAD+∠CAE﹣∠BAC或∠DAE=∠BAC﹣∠BAD﹣∠CAE,即可求得∠BAC的度数.
【解答】解:①如图,当∠BAC为锐角时,
∵DF是AB的垂直平分线,EG是AC的垂直平分线,
∴DA=DB,EC=EA,
∴∠B=∠BAD,∠C=∠CAE,
∵∠DAE=∠BAD+∠CAE﹣∠BAC,且∠DAE=30°,
∴30°=∠B+∠C﹣∠BAC,
即30°=(180°﹣∠BAC)﹣∠BAC,
解得∠BAC=75°.
②当∠BAC为钝角时,
∵DF是线段AB的垂直平分线,
∴DA=DB,
∴∠B=∠DAB,
同理∠C=∠EAC,
∵∠B+∠DAB+∠C+∠EAC+∠DAE=180°,
∴∠DAB+∠EAC=(180°﹣30°)=75°,
∴∠BAC=180°﹣75°=105°,
故答案为:75°或105°.
13.如图,DE是△ABC边AC的垂直平分线,若BC=8,AD=3,则BD= 5 .
【考点】线段垂直平分线的性质.
【分析】根据垂直平分线的性质可得D=CD,进而求出BD的长度.
【解答】解:∵DE是△ABC边AC的垂直平分线,
∴AD=CD,
∵BC=8,AD=3,
∴BD=BC﹣CD=BC﹣AD=8﹣3=5,
故答案为:5.
14.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,在格纸中能画出与△ABC成轴对称且也以格点为顶点的三角形(不包括△ABC本身),这样的三角形共有 3 个
【考点】轴对称的性质.
【分析】依据大正方形的对称轴,即可画出与△ABC成轴对称且也以格点为顶点的三角形.
【解答】解:如图所示,与△ABC成轴对称且也以格点为顶点的三角形有3个:
故答案为:3.
15.如图,在正方形ABCD中,有面积为4的正方形EFGH和面积为2的正方形PQMN,点E、F、P、Q分别在边AB、BC、CD、AD上,点M、N在边HG上,且组成的图形为轴对称图形,则正方形ABCD的面积为 + .
【考点】轴对称图形.
【分析】连接BD,交PQ于R,交HG于S,交EF于K,依据轴对称图形的性质,即可得到BD的长,进而得到正方形ABCD的面积.
【解答】解:如图,连接BD,交PQ于R,交HG于S,交EF于K,
∵正方形ABCD中,有面积为4的正方形EFGH和面积为2的正方形PQMN,
∴EH=EF=2,MQ=QP=,
又∵组成的图形为轴对称图形,
∴BD为对称轴,
∴△BEF、△DPQ为等腰直角三角形,四边形EKSH、四边形MSRQ为矩形,
∴EK=BK=EF=1,DR=QR=PQ=,KN=EH=2,RS=MQ=,
∴BD=1+2++=3+,
∴正方形ABCD的面积=BD2=×(3+)2=+,
故答案为:+.
三.解答题(共5小题)
16.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB,BC于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
【考点】线段垂直平分线的性质.
【分析】(1)依据线段垂直平分线的性质,即可得到△CDE的周长=CD+DE+CE=AD+DE+BE=AB;
(2)依据AD=CD,BE=CE,即可得到∠A=∠ACD,∠B=∠BCE,再根据三角形内角和定理,即可得到∠A+∠B=55°,进而得到∠ACD+∠BCE=55°,再根据∠DCE=∠ACB﹣(∠ACD+∠BCE)进行计算即可.
【解答】解:(1)△CDE的周长为10.
∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;
(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴∠A=∠ACD,∠B=∠BCE,
又∵∠ACB=125°,
∴∠A+∠B=180°﹣125°=55°,
∴∠ACD+∠BCE=55°,
∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.
17.如图,在△ABC中,∠C=90°,DE为AB的垂直平分线,DE交AC于点D,连接BD.若∠ABD=2∠CBD,求∠A的度数.
【考点】线段垂直平分线的性质.
【分析】依据线段垂直平分线的性质,可得∠A=∠ABD=2∠CBD,设∠A=α,则∠ABD=α,∠CBD=α,依据三角形内角和定理,即可得到∠A的度数.
【解答】解:∵DE为AB的垂直平分线,
∴∠A=∠ABD,
又∵∠ABD=2∠CBD,
∴∠A=∠ABD=2∠CBD,
设∠A=α,则∠ABD=α,∠CBD=α,
又∵∠C=90°,
∴∠A+∠ABC=90°,
即α+α+α=90°,
解得α=36°,
∴∠A=36°.
18.已知:如图,AF平分∠BAC,BC垂直平分AD,垂足为E,CF上一点P,连结PB交线段AF相交于点M.
(1)求证:AB∥CD;
(2)若∠DAC=∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
【考点】平行线的判定与性质;线段垂直平分线的性质.
【分析】(1)依据垂直平分线的性质以及角平分线的定义,即可得到∠CDA=∠BAD,即可得到AB∥CD;
(2)判定△ACE≌△ABE,可得AC=AB.再判定△ACM≌△ABM,可得∠AMC=∠AMB,再根据三角形内角和定理,即可得到∠F=∠MCD.
【解答】解:(1)∵BC垂直平分AD,
∴AC=CD,∠CAD=∠CDA,
∵AF平分∠BAC,
∴∠CAD=∠BAD,
∴∠CDA=∠BAD,
∴AB∥CD;
(2)结论:∠F=∠MCD,
理由:∵∠DAC=∠CDA,∠DAC=∠MPC,
∴∠CDA=∠MPC,
又∵∠CDA+∠CDM=180°,∠MPC+∠MPF=180°,
∴∠CDM=∠MPF;
又∵AF平分∠BAC,AE⊥BC,AE=AE.
∴△ACE≌△ABE(ASA),
∴AC=AB.
又∵AF平分∠BAC,AM=AM,
∴△ACM≌△ABM(SAS),
∴∠AMC=∠AMB,
又∵∠AMB=∠PMF.
∴∠AMC=∠PMF.
又∵∠AMC+∠MCD+∠CDM=180°,∠PMF+∠MPF+∠F=180°,
∴∠F=∠MCD.
19.如图,在△ABC中,∠ABC=45°,点P为边BC上的一点,BC=3BP,且∠PAB=15°点C关于直线PA的对称点为D,连接BD,又△APC的PC边上的高为AH
(1)求∠BPD的大小;
(2)判断直线BD,AH是否平行?并说明理由;
(3)证明:∠BAP=∠CAH.
【考点】平行线的判定与性质;轴对称的性质.
【分析】(1)根据点C关于直线PA的对称点为D,即可得到△ADP≌△ACP,进而得出∠APC=∠APD=60°,即可得到∠BPD=180°﹣120°=60°;
(2)先取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,进而得到∠DBP=90°,即BD⊥BC.再根据△APC的PC边上的高为AH,可得AH⊥BC,进而得出BD∥AH;
(3)过点A作BD、DP的垂线,垂足分别为G、F.根据∠GBA=∠CBA=45°,可得点A在∠GBC的平分线上,进而得到点A在∠GDP的平分线上.再根据∠GDP=150°,即可得到∠C=∠ADP=75°,进而得到Rt△ACH中,∠CAH=15°,即可得出∠BAP=∠CAH.
【解答】解:(1)∵∠PAB=15°,∠ABC=45°,
∴∠APC=15°+45°=60°,
∵点C关于直线PA的对称点为D,
∴PD=PC,AD=AC,
∴△ADP≌△ACP,
∴∠APC=∠APD=60°,
∴∠BPD=180°﹣120°=60°;
(2)直线BD,AH平行.理由:
∵BC=3BP,
∴BP=PC=PD,
如图,取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,
∴∠BEP=60°,
∴∠BDE=∠BEP=30°,
∴∠DBP=90°,即BD⊥BC.
又∵△APC的PC边上的高为AH,
∴AH⊥BC,
∴BD∥AH;
(3)如图,过点A作BD、DP的垂线,垂足分别为G、F.
∵∠APC=∠APD,即点A在∠DPC的平分线上,
∴AH=AF.
∵∠CBD=90°,∠ABC=45°,
∴∠GBA=∠CBA=45°,
即点A在∠GBC的平分线上,
∴AG=AH,
∴AG=AF,
∴点A在∠GDP的平分线上.
又∵∠BDP=30°,
∴∠GDP=150°,
∴∠ADP=×150°=75°,
∴∠C=∠ADP=75°,
∴Rt△ACH中,∠CAH=15°,
∴∠BAP=∠CAH.
20.(1)请找出下图中每个正多边形对称轴的条数,并填入下表.
正多边形的边数
3
4
5
6
8
…
对称轴的条数
3
4
5
…
(2)请写出正多边形的对称轴的条数y随正多边形的边数n(n≥3)变化的关系式 y=n .
【考点】轴对称图形.
【分析】(1)观察出正三角形的对称轴有3条,正方形有4条对称轴,正5边形有5条对称轴,再分别画出正6、8边形的对称轴即可推出答案;
(2)根据正三角形的对称轴有3条,正方形有4条对称轴,正5边形有5条对称轴等等,即可找出规律﹣﹣正多边形得边数和对称轴的条数相等,即可写出答案.
【解答】答(1)
正多边形的边数
3
4
5
6
8
…
对称轴的条数
3
4
5
6
8
…
故答案为:6,8.
解:(2)y=n(n≥3)
故答案为:y=n.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
13.1
轴对称
高频易错题汇编
一.选择题(共10小题)
1.如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于点D.若AD=5,CD=3,则BC长是( )
A.7
B.8
C.12
D.13
2.如图,在△ABC中,DE垂直平分AC,若BC=22cm,AB=14cm,则△ABD的周长为( )
A.24cm
B.25cm
C.30cm
D.36cm
3.如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数( )
A.40°
B.70°
C.30°
D.50°
4.如图,在△ABC中,∠A=90°,∠C=30°,PQ垂直平分BC,与AC交于点P,下列结论正确的是( )
A.PC<2PA
B.PC>2PA
C.AB<2PA
D.AB>2PA
5.已知锐角三角形ABC中,∠A=65°,点O是AB、AC垂直平分线的交点,则∠BCO的度数是( )
A.25°
B.30°
C.35°
D.40°
6.视力表中的字母“E”有各种不同的摆放形式,下面每种组合中的两个字母“E”不能关于某条直线成轴对称的是( )
A.
B.
C.
D.
7.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1
B.2
C.3
D.4
8.如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( )
A.5个
B.6个
C.7个
D.8个
9.如图,直线MN是四边形MANB的对称轴,点P在MN上.则下列结论错误的是( )
A.∠ANM=∠BNM
B.∠MAP=∠MBP
C.AM=BM
D.AP=BN
10.下列图形,轴对称图形有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共5小题)
11.如图,在△ABC中,∠B=40°,∠C=45°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,则∠DAE=
.
12.△ABC中,DF是AB的垂直平分线,交BC于D,EG是AC的垂直平分线,交BC于E,若∠DAE=30°,则∠BAC等于
.
13.如图,DE是△ABC边AC的垂直平分线,若BC=8,AD=3,则BD=
.
14.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,在格纸中能画出与△ABC成轴对称且也以格点为顶点的三角形(不包括△ABC本身),这样的三角形共有
个
15.如图,在正方形ABCD中,有面积为4的正方形EFGH和面积为2的正方形PQMN,点E、F、P、Q分别在边AB、BC、CD、AD上,点M、N在边HG上,且组成的图形为轴对称图形,则正方形ABCD的面积为
.
三.解答题(共5小题)
16.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB,BC于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
17.如图,在△ABC中,∠C=90°,DE为AB的垂直平分线,DE交AC于点D,连接BD.若∠ABD=2∠CBD,求∠A的度数.
18.已知:如图,AF平分∠BAC,BC垂直平分AD,垂足为E,CF上一点P,连结PB交线段AF相交于点M.
(1)求证:AB∥CD;
(2)若∠DAC=∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
19.如图,在△ABC中,∠ABC=45°,点P为边BC上的一点,BC=3BP,且∠PAB=15°点C关于直线PA的对称点为D,连接BD,又△APC的PC边上的高为AH
(1)求∠BPD的大小;
(2)判断直线BD,AH是否平行?并说明理由;
(3)证明:∠BAP=∠CAH.
20.(1)请找出下图中每个正多边形对称轴的条数,并填入下表.
正多边形的边数
3
4
5
6
8
…
对称轴条数
3
4
5
…
(2)请写出正多边形的对称轴的条数y随正多边形的边数n(n≥3)变化的关系式
.
试题解析
一.选择题(共10小题)
1.如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于点D.若AD=5,CD=3,则BC长是( )
A.7
B.8
C.12
D.13
【考点】线段垂直平分线的性质.
【分析】由尺规作图可知,MN是线段AB的垂直平分线,即可得出DA=DB=5,依据CD的长即可得到BC=CD+BD=8.
【解答】解:由尺规作图可知,MN是线段AB的垂直平分线,
∴DA=DB=5,
又∵CD=3,
∴BC=CD+BD=3+5=8,
故选:B.
2.如图,在△ABC中,DE垂直平分AC,若BC=22cm,AB=14cm,则△ABD的周长为( )
A.24cm
B.25cm
C.30cm
D.36cm
【考点】线段垂直平分线的性质.
【分析】根据线段的垂直平分线的性质得到DA=DC,根据三角形的周长公式计算即可.
【解答】解:∵DE垂直平分AC,
∴DA=DC,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=36(cm).
故选:D.
3.如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数( )
A.40°
B.70°
C.30°
D.50°
【考点】线段垂直平分线的性质.
【分析】根据等腰三角形的性质、三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到DA=DB,得到∠DBA=∠A=40°,计算即可.
【解答】解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵MN是AB的垂直平分线,
∴DA=DB,
∴∠DBA=∠A=40°,
∴∠DBC=30°,
故选:C.
4.如图,在△ABC中,∠A=90°,∠C=30°,PQ垂直平分BC,与AC交于点P,下列结论正确的是( )
A.PC<2PA
B.PC>2PA
C.AB<2PA
D.AB>2PA
【考点】三角形三边关系;线段垂直平分线的性质.
【分析】连接BP,根据三角形内角和定理求出∠ABC=60°,根据线段垂直平分线的性质得到PB=PC,得到∠PBC=∠C=30°,根据直角三角形的性质、三角形的三边关系解答即可.
【解答】解:连接BP,
∵∠A=90°,∠C=30°,
∴∠ABC=60°,
∵PQ垂直平分BC,
∴PB=PC,
∴∠PBC=∠C=30°,
∴∠ABP=30°,
∴AP=BP=PC,
∴PC=2PA,故A、B选项错误;
∵∠A=90°,
∴AB<PB<2PA,
∴C正确,D错误;
故选:C.
5.已知锐角三角形ABC中,∠A=65°,点O是AB、AC垂直平分线的交点,则∠BCO的度数是( )
A.25°
B.30°
C.35°
D.40°
【考点】线段垂直平分线的性质.
【分析】连接OA、OB,根据三角形内角和定理求出∠ABC+∠ACB=115°,根据线段的垂直平分线的性质得到OA=OB,OA=OC,根据等腰三角形的性质计算即可.
【解答】解:如图,连接OA、OB,
∵∠BAC=65°,
∴∠ABC+∠ACB=115°,
∵O是AB,AC垂直平分线的交点,
∴OA=OB,OA=OC,
∴∠OAB=∠OBA,∠OCA=∠OAC,OB=OC,
∴∠OBA+∠OCA=65°,
∴∠OBC+∠OCB=115°﹣65°=50°,
∵OB=OC,
∴∠BCO=∠CBO=25°,
故选:A.
6.视力表中的字母“E”有各种不同的摆放形式,下面每种组合中的两个字母“E”不能关于某条直线成轴对称的是( )
A.
B.
C.
D.
【考点】生活中的轴对称现象.
【分析】把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也称轴对称,这条直线叫做对称轴.
【解答】解:A,B,D选项中,两个字母“E”关于直线l成轴对称,而C选项中,两个字母“E”不能沿着某条直线翻折互相重合.
故选:C.
7.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1
B.2
C.3
D.4
【考点】生活中的轴对称现象.
【分析】根据题意画出图形,由轴对称的性质判定正确选项.
【解答】解:根据轴对称的性质可知,台球走过的路径为:
∴该球最后将落入的球袋是4号.
故选:D.
8.如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( )
A.5个
B.6个
C.7个
D.8个
【考点】轴对称的性质.
【分析】依据对称轴的不同位置,即可得到位置不同的三角形.
【解答】解:如图所示:
与△ABC成轴对称,顶点在格点上,且位置不同的三角形有8个,
故选:D.
9.如图,直线MN是四边形MANB的对称轴,点P在MN上.则下列结论错误的是( )
A.∠ANM=∠BNM
B.∠MAP=∠MBP
C.AM=BM
D.AP=BN
【考点】轴对称的性质.
【分析】根据直线MN是四边形AMBN的对称轴,得到点A与点B对应,根据轴对称的性质即可得到结论.
【解答】解:∵直线MN是四边形AMBN的对称轴,
∴点A与点B对应,
∴AM=BM,AN=BN,∠ANM=∠BNM,
∵点P是直线MN上的点,
∴∠MAP=∠MBP,
∴A,B,C正确,而D错误,
故选:D.
10.下列图形,轴对称图形有( )
A.1个
B.2个
C.3个
D.4个
【考点】轴对称图形.
【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时也可以说这个图形关于这条直线(成轴)对称.
【解答】解:由图可得,第一个图是轴对称图形;
第二个图是轴对称图形;
第三个图是轴对称图形;
第四个图不是轴对称图形;
所以轴对称图形有3个,
故选:C.
二.填空题(共5小题)
11.如图,在△ABC中,∠B=40°,∠C=45°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,则∠DAE= 10° .
【考点】线段垂直平分线的性质.
【分析】根据线段的垂直平分线得出AD=BD,AE=CE,推出∠B=∠BAD,∠C=∠CAE,求出∠BAD+∠CAE的度数即可得到答案.
【解答】解:∵点D、E分别是AB、AC边的垂直平分线与BC的交点,
∴AD=BD,AE=CE,
∴∠B=∠BAD,∠C=∠CAE,
∵∠B=40°,∠C=45°,
∴∠B+∠C=85°,∠BAC=95°,
∴∠BAD+∠CAE=85°,
∴∠DAE=∠BAC﹣(∠BAD+∠CAE)=95°﹣85°=10°,
故答案为:10°
12.△ABC中,DF是AB的垂直平分线,交BC于D,EG是AC的垂直平分线,交BC于E,若∠DAE=30°,则∠BAC等于 75°或105° .
【考点】三角形内角和定理;线段垂直平分线的性质.
【分析】分两种情况讨论:∠BAC为锐角,∠BAC为钝角.先根据线段垂直平分线的性质,得出DA=DB,EC=EA,得到∠B=∠BAD,∠C=∠CAE,再根据关系式∠DAE=∠BAD+∠CAE﹣∠BAC或∠DAE=∠BAC﹣∠BAD﹣∠CAE,即可求得∠BAC的度数.
【解答】解:①如图,当∠BAC为锐角时,
∵DF是AB的垂直平分线,EG是AC的垂直平分线,
∴DA=DB,EC=EA,
∴∠B=∠BAD,∠C=∠CAE,
∵∠DAE=∠BAD+∠CAE﹣∠BAC,且∠DAE=30°,
∴30°=∠B+∠C﹣∠BAC,
即30°=(180°﹣∠BAC)﹣∠BAC,
解得∠BAC=75°.
②当∠BAC为钝角时,
∵DF是线段AB的垂直平分线,
∴DA=DB,
∴∠B=∠DAB,
同理∠C=∠EAC,
∵∠B+∠DAB+∠C+∠EAC+∠DAE=180°,
∴∠DAB+∠EAC=(180°﹣30°)=75°,
∴∠BAC=180°﹣75°=105°,
故答案为:75°或105°.
13.如图,DE是△ABC边AC的垂直平分线,若BC=8,AD=3,则BD= 5 .
【考点】线段垂直平分线的性质.
【分析】根据垂直平分线的性质可得D=CD,进而求出BD的长度.
【解答】解:∵DE是△ABC边AC的垂直平分线,
∴AD=CD,
∵BC=8,AD=3,
∴BD=BC﹣CD=BC﹣AD=8﹣3=5,
故答案为:5.
14.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,在格纸中能画出与△ABC成轴对称且也以格点为顶点的三角形(不包括△ABC本身),这样的三角形共有 3 个
【考点】轴对称的性质.
【分析】依据大正方形的对称轴,即可画出与△ABC成轴对称且也以格点为顶点的三角形.
【解答】解:如图所示,与△ABC成轴对称且也以格点为顶点的三角形有3个:
故答案为:3.
15.如图,在正方形ABCD中,有面积为4的正方形EFGH和面积为2的正方形PQMN,点E、F、P、Q分别在边AB、BC、CD、AD上,点M、N在边HG上,且组成的图形为轴对称图形,则正方形ABCD的面积为 + .
【考点】轴对称图形.
【分析】连接BD,交PQ于R,交HG于S,交EF于K,依据轴对称图形的性质,即可得到BD的长,进而得到正方形ABCD的面积.
【解答】解:如图,连接BD,交PQ于R,交HG于S,交EF于K,
∵正方形ABCD中,有面积为4的正方形EFGH和面积为2的正方形PQMN,
∴EH=EF=2,MQ=QP=,
又∵组成的图形为轴对称图形,
∴BD为对称轴,
∴△BEF、△DPQ为等腰直角三角形,四边形EKSH、四边形MSRQ为矩形,
∴EK=BK=EF=1,DR=QR=PQ=,KN=EH=2,RS=MQ=,
∴BD=1+2++=3+,
∴正方形ABCD的面积=BD2=×(3+)2=+,
故答案为:+.
三.解答题(共5小题)
16.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB,BC于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
【考点】线段垂直平分线的性质.
【分析】(1)依据线段垂直平分线的性质,即可得到△CDE的周长=CD+DE+CE=AD+DE+BE=AB;
(2)依据AD=CD,BE=CE,即可得到∠A=∠ACD,∠B=∠BCE,再根据三角形内角和定理,即可得到∠A+∠B=55°,进而得到∠ACD+∠BCE=55°,再根据∠DCE=∠ACB﹣(∠ACD+∠BCE)进行计算即可.
【解答】解:(1)△CDE的周长为10.
∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;
(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴∠A=∠ACD,∠B=∠BCE,
又∵∠ACB=125°,
∴∠A+∠B=180°﹣125°=55°,
∴∠ACD+∠BCE=55°,
∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.
17.如图,在△ABC中,∠C=90°,DE为AB的垂直平分线,DE交AC于点D,连接BD.若∠ABD=2∠CBD,求∠A的度数.
【考点】线段垂直平分线的性质.
【分析】依据线段垂直平分线的性质,可得∠A=∠ABD=2∠CBD,设∠A=α,则∠ABD=α,∠CBD=α,依据三角形内角和定理,即可得到∠A的度数.
【解答】解:∵DE为AB的垂直平分线,
∴∠A=∠ABD,
又∵∠ABD=2∠CBD,
∴∠A=∠ABD=2∠CBD,
设∠A=α,则∠ABD=α,∠CBD=α,
又∵∠C=90°,
∴∠A+∠ABC=90°,
即α+α+α=90°,
解得α=36°,
∴∠A=36°.
18.已知:如图,AF平分∠BAC,BC垂直平分AD,垂足为E,CF上一点P,连结PB交线段AF相交于点M.
(1)求证:AB∥CD;
(2)若∠DAC=∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
【考点】平行线的判定与性质;线段垂直平分线的性质.
【分析】(1)依据垂直平分线的性质以及角平分线的定义,即可得到∠CDA=∠BAD,即可得到AB∥CD;
(2)判定△ACE≌△ABE,可得AC=AB.再判定△ACM≌△ABM,可得∠AMC=∠AMB,再根据三角形内角和定理,即可得到∠F=∠MCD.
【解答】解:(1)∵BC垂直平分AD,
∴AC=CD,∠CAD=∠CDA,
∵AF平分∠BAC,
∴∠CAD=∠BAD,
∴∠CDA=∠BAD,
∴AB∥CD;
(2)结论:∠F=∠MCD,
理由:∵∠DAC=∠CDA,∠DAC=∠MPC,
∴∠CDA=∠MPC,
又∵∠CDA+∠CDM=180°,∠MPC+∠MPF=180°,
∴∠CDM=∠MPF;
又∵AF平分∠BAC,AE⊥BC,AE=AE.
∴△ACE≌△ABE(ASA),
∴AC=AB.
又∵AF平分∠BAC,AM=AM,
∴△ACM≌△ABM(SAS),
∴∠AMC=∠AMB,
又∵∠AMB=∠PMF.
∴∠AMC=∠PMF.
又∵∠AMC+∠MCD+∠CDM=180°,∠PMF+∠MPF+∠F=180°,
∴∠F=∠MCD.
19.如图,在△ABC中,∠ABC=45°,点P为边BC上的一点,BC=3BP,且∠PAB=15°点C关于直线PA的对称点为D,连接BD,又△APC的PC边上的高为AH
(1)求∠BPD的大小;
(2)判断直线BD,AH是否平行?并说明理由;
(3)证明:∠BAP=∠CAH.
【考点】平行线的判定与性质;轴对称的性质.
【分析】(1)根据点C关于直线PA的对称点为D,即可得到△ADP≌△ACP,进而得出∠APC=∠APD=60°,即可得到∠BPD=180°﹣120°=60°;
(2)先取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,进而得到∠DBP=90°,即BD⊥BC.再根据△APC的PC边上的高为AH,可得AH⊥BC,进而得出BD∥AH;
(3)过点A作BD、DP的垂线,垂足分别为G、F.根据∠GBA=∠CBA=45°,可得点A在∠GBC的平分线上,进而得到点A在∠GDP的平分线上.再根据∠GDP=150°,即可得到∠C=∠ADP=75°,进而得到Rt△ACH中,∠CAH=15°,即可得出∠BAP=∠CAH.
【解答】解:(1)∵∠PAB=15°,∠ABC=45°,
∴∠APC=15°+45°=60°,
∵点C关于直线PA的对称点为D,
∴PD=PC,AD=AC,
∴△ADP≌△ACP,
∴∠APC=∠APD=60°,
∴∠BPD=180°﹣120°=60°;
(2)直线BD,AH平行.理由:
∵BC=3BP,
∴BP=PC=PD,
如图,取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,
∴∠BEP=60°,
∴∠BDE=∠BEP=30°,
∴∠DBP=90°,即BD⊥BC.
又∵△APC的PC边上的高为AH,
∴AH⊥BC,
∴BD∥AH;
(3)如图,过点A作BD、DP的垂线,垂足分别为G、F.
∵∠APC=∠APD,即点A在∠DPC的平分线上,
∴AH=AF.
∵∠CBD=90°,∠ABC=45°,
∴∠GBA=∠CBA=45°,
即点A在∠GBC的平分线上,
∴AG=AH,
∴AG=AF,
∴点A在∠GDP的平分线上.
又∵∠BDP=30°,
∴∠GDP=150°,
∴∠ADP=×150°=75°,
∴∠C=∠ADP=75°,
∴Rt△ACH中,∠CAH=15°,
∴∠BAP=∠CAH.
20.(1)请找出下图中每个正多边形对称轴的条数,并填入下表.
正多边形的边数
3
4
5
6
8
…
对称轴的条数
3
4
5
…
(2)请写出正多边形的对称轴的条数y随正多边形的边数n(n≥3)变化的关系式 y=n .
【考点】轴对称图形.
【分析】(1)观察出正三角形的对称轴有3条,正方形有4条对称轴,正5边形有5条对称轴,再分别画出正6、8边形的对称轴即可推出答案;
(2)根据正三角形的对称轴有3条,正方形有4条对称轴,正5边形有5条对称轴等等,即可找出规律﹣﹣正多边形得边数和对称轴的条数相等,即可写出答案.
【解答】答(1)
正多边形的边数
3
4
5
6
8
…
对称轴的条数
3
4
5
6
8
…
故答案为:6,8.
解:(2)y=n(n≥3)
故答案为:y=n.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
