高中数学人教A版必修二4.1.2圆的一般方程 课件(共24张PPT)
文档属性
| 名称 | 高中数学人教A版必修二4.1.2圆的一般方程 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 20:36:57 | ||
图片预览








文档简介
(共24张PPT)
4.1
圆的方程
4.1.2
圆的一般方程
一、
圆的标准方程是怎样的?
圆心为(a,b),半径为r时
(x?a)2
+
(y
?b)2
=
r2
特别地,
圆心在原点时,
x2
+y2
=
r2
复习回顾
x
O
y
A(a,b)
r
x
O
y
r
说明:
圆的方程有三个独立参数:a,b,r,因此确定一个圆需要三个条件。
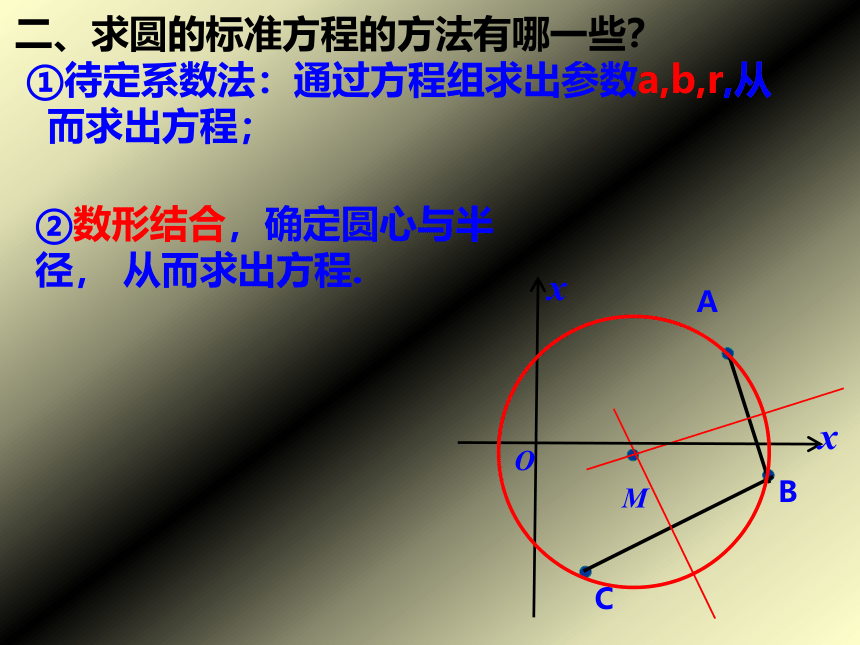
二、求圆的标准方程的方法有哪一些?
①待定系数法:通过方程组求出参数a,b,r,从而求出方程;
M
A
B
C
x
O
x
②数形结合,确定圆心与半径,
从而求出方程.
1.想一想,若把圆的标准方程(x-a)
2
+
(y-b)
2
=
r2展开后,会得出怎样的形式?由此你能得到什么结论?
任何一个圆的方程都是二元二次方程。
探究新知
2.下列二元二次方程各表示什么图形?由此你能得到什么结论?
(1)x2+y2
-2x-
4y
+1=0
(2)x2+y2
-2x-4y+6=0
方程可化为(x-1)2+(y-2)2=4,
表示圆心为(1,-2),半径为2的圆
方程可化为(x-1)2+(y-2)2=-1,
不表示任何图形
(3)x2+y2
-2x-4y+5=0
方程可化为(x-1)2+(y-2)2=0,
表示点(1,2)
一个二元二次方程可能是一个圆的方程,也能不是。
将x2+y2+Dx+
Ey+F
=0配方整理可得:
3.那么,二元二次方程x2+y2+Dx+
Ey+F
=0
在什么条件下表示圆?
4.
将上式与圆的标准方程
(x?a)2
+
(y
?b)2
=
r2
相比较,你能得出什么结论?
1.圆的一般方程:
D2+E2-4F>0
半径为:
3.标准方程与一般方程比较:
两种方程都有三个独立的参数;但标准方程带有明显的几何特征,一般方程的代数特征更明显的。
圆的一般方程
x2+y2+Dx+
Ey+F
=0(当D2+E2-4F>0时)
(2)圆心:
(1)条件
:
1.下列方程各表示什么图形?
原点(0,0)
练习
例析
例1.求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求出这个圆的圆心坐标和半径.
解:设所求的圆的方程为(x-a)2+(y-b)2=r2.
∵O、M1、M2三点在圆上,
∴它们的坐标满足方程
∴所求圆的方程为:(x-4)2+(y+3)2=52,
∴圆心坐标(4,-3),半径为r=5.
用一般式方程可以吗?
解此方程组,可得:a=-4,b=3,r2=25.
例1.求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求出这个圆的圆心坐标和半径.
另解:设所求的圆的方程为x2+y2+Dx+Ey+F=0(其中D2+E2-4F
>0).
∵O、M1、M2三点在圆上,
∴它们的坐标满足方程
即(x-4)2+(y+3)2=52,
∴圆心坐标(4,-3),半径为r=5.
与用标准式相比,有何特点?
解此方程组得:
D=-8,E=6,F=0.
∴所求圆的方程为:x2+y2-8x+6y=0.
思考:本题还有其它解法吗?
1.待定系数法:
(1)根据题意选择标准方程和一般方程;
若所给的条件与圆心和半径有直接关系,设为标准方程;
若条件主要是圆所经过的点的坐标,则宜用一般方程
(2)根据条件列出关于a,b,r或D,E,F的方程组。
(3)解出a,b,r或D,E,F,再求出圆方程。
2.数形结合:
结合图形,根据圆的性质相关求出圆心和半径,从而求出的方程
。
求圆方程的方法
练习
(1)方程x2+y2+Dx+Ey+F=0表示的曲线是以(-2,3)为圆心,4为半径的圆.求D、E、F的值
D=4,E=-6,F=-3
(
2)用待定系数法求出经过点A(1,-1)、B(1,4)、C(4,-2)的圆的方程.
x2+y2-7x-3y+2=0.
(
3)“求经过点A(4,-5),且与直线m:x-2y+4=0相切于点B(-2,1)的圆的方程”,有哪一些方法?
XJ
ZY
LX
例2.已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程
(x0,y0)
(x,y)
例析
.
O
x
y
.B(4,3)
.
.
M
A
解:
设点M为(x,y),点A为(x0,y0)
由中点坐标公式得
∴x0=2x-4,y0=2y-3,
即A(2x-4,2y-3)
∵A在圆(x+1)2+y2=4上
∴[(2x-4)+1]2+(2y-3)2=4,
∴线段AB的中点M的轨迹方程为
坐标代入法
(相关点法)
思考:这种方法的主要过程是怎样?
XJ
ZY
LX
例2.已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程
(x0,y0)
(x,y)
.
O
x
y
.B(4,3)
.
.
M
A
解:
设点M为(x,y),点A为(x0,y0)
由中点坐标公式得
∴x0=2x-4,y0=2y-3,
即A(2x-4,2y-3)
∵A在圆(x+1)2+y2=4上
∴[(2x-4)+1]2+(2y-3)2=4,
∴线段AB的中点M的轨迹方程为
归纳:
用坐标代入法
(相关点法)求方程的大致步骤:
(1)设出所求轨迹上任意一点和已知图形上相关点的坐标;(设坐标)
(2)根据条件用所求轨迹上任意一点的坐标将已知图形上点的坐标表示出来。(求坐标)
(3)将已知图形上点的坐标代入已知图形的方程并化简。(代入化简)
(4)
验证有无特殊情况
(验证)
XJ
ZY
LX
已知线段AB的端点B的坐标是(3,0),端点A在圆x2+y2=16上运动,P在直线AB上,且
求P的轨迹方程
(x0,y0)
(x,y)
练习
.
O
x
y
.
B(3,0)
.
.
P
A
解:
设点P为(x,y),点A为(x0,y0)
∴x0=9-2x,y0=2y
即A(9-2x,2y)
∵A在圆x2+y2=16上
∴(9-2x)2+(2y)2=16,
∴线段AB的中点M的轨迹方程为
XJ
ZY
LX
例3.经过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆
C于A、B两点,求线段AB的中点P的轨迹.
解:圆C的方程可化为(x-3)2+(y-2)2=4,其圆心为C(3,2),半径为2.
设P(x,y)是轨迹上任意一点.
∵CP⊥MP
∴当x≠3时,kCP?kMP=-1,即
化简得x2+y2+3x-2y-18=0,
经验证,当x=3时,此方程也成立
∴P的轨迹为圆x2+y2+3x-2y-18=0在圆C内部的一段圆弧.
直译法
思考:直译法的一般步骤是什么?
第一步,建系,设点;
第二步,找出点满足的几何条件;
第三步,将几何条件转化为代数条件;
第四步,化简;
第五步,验证有无特殊情况
.
XJ
ZY
LX
例析
已知点P到直线y+2=0和点F(1,1)点的距离相等;求证点P的轨迹是抛物线。
.
F(1,1)
(x,y)
练习
O
x
y
.
P
解:
设点P为(x,y),点P到m的距离为d
即
∴点M的轨迹为开口向上,对称轴为x=1的抛物线。
XJ
ZY
LX
由题意得,
y=-2
d=|PF|
练习
教材P123
练习
1,3题
XJ
ZY
P124
习题4.1
B组1,2
小结
一、
圆的方程:
1.标准方程:
(x?a)2
+
(y
?b)2
=
r2
特别地,
圆心在原点时,
x2
+y2
=
r2
2.圆的一般方程:
半径为:
圆心为:
圆心为:
(a,b)
半径为:
r
x2+y2+Dx+
Ey+F
=0(当D2+E2-4F>0时)
ZY
三、求圆方程的方法:
1.待定系数法:
(1)根据题意选择标准方程和一般方程;
若所给的条件与圆心和半径有直接关系,设为标准方程;
若条件主要是圆所经过的点的坐标,则宜用一般方程
(2)根据条件列出关于a,b,r或D,E,F的方程组。
(3)解出a,b,r或D,E,F,再求出圆方程。
2.数形结合:
结合图形,根据圆的性质求出圆心和半径,从而求出的方程时
。
ZY
四、用坐标代入法
(相关点法)求轨迹方程的主要步骤:
(1)设出所求轨迹上任意一点和已知图形上相关点的坐标;(建系设坐标)
(2)根据条件用所求轨迹上任意一点的坐标将已知图形上点的坐标表示出来。(求坐标)
(3)将已知图形上点的坐标代入已知图形的方程并化简。(代入化简)
(4)
验证有无特殊情况
(验证)
ZY
五、用直译法求轨迹方程的主要步骤:
(1)建立坐标系,设出该点坐标;
(2)找出点满足的几何条件;
(3)将几何条件转化为代数条件;
(4)将方程化简变形;
(5)验证有无特殊情况。
ZY
2.若圆C1:x2+y2=4和圆C2:x2+y2+4x-4y+4=0关于直线m对称。求直线
m的方程。
作业
1.已知圆过原点O(0,0)和点P(3,-1),且圆心在3x+y=5上,求此圆方程。
3.若P是圆O:x2+y2=4上一个动点,定点M为(4,4)。
(1)若OQ⊥QM,求点Q的轨迹的方程。
(2)若M始终是线段PQ的中点。求点Q的轨迹的方程。
4.1
圆的方程
4.1.2
圆的一般方程
一、
圆的标准方程是怎样的?
圆心为(a,b),半径为r时
(x?a)2
+
(y
?b)2
=
r2
特别地,
圆心在原点时,
x2
+y2
=
r2
复习回顾
x
O
y
A(a,b)
r
x
O
y
r
说明:
圆的方程有三个独立参数:a,b,r,因此确定一个圆需要三个条件。
二、求圆的标准方程的方法有哪一些?
①待定系数法:通过方程组求出参数a,b,r,从而求出方程;
M
A
B
C
x
O
x
②数形结合,确定圆心与半径,
从而求出方程.
1.想一想,若把圆的标准方程(x-a)
2
+
(y-b)
2
=
r2展开后,会得出怎样的形式?由此你能得到什么结论?
任何一个圆的方程都是二元二次方程。
探究新知
2.下列二元二次方程各表示什么图形?由此你能得到什么结论?
(1)x2+y2
-2x-
4y
+1=0
(2)x2+y2
-2x-4y+6=0
方程可化为(x-1)2+(y-2)2=4,
表示圆心为(1,-2),半径为2的圆
方程可化为(x-1)2+(y-2)2=-1,
不表示任何图形
(3)x2+y2
-2x-4y+5=0
方程可化为(x-1)2+(y-2)2=0,
表示点(1,2)
一个二元二次方程可能是一个圆的方程,也能不是。
将x2+y2+Dx+
Ey+F
=0配方整理可得:
3.那么,二元二次方程x2+y2+Dx+
Ey+F
=0
在什么条件下表示圆?
4.
将上式与圆的标准方程
(x?a)2
+
(y
?b)2
=
r2
相比较,你能得出什么结论?
1.圆的一般方程:
D2+E2-4F>0
半径为:
3.标准方程与一般方程比较:
两种方程都有三个独立的参数;但标准方程带有明显的几何特征,一般方程的代数特征更明显的。
圆的一般方程
x2+y2+Dx+
Ey+F
=0(当D2+E2-4F>0时)
(2)圆心:
(1)条件
:
1.下列方程各表示什么图形?
原点(0,0)
练习
例析
例1.求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求出这个圆的圆心坐标和半径.
解:设所求的圆的方程为(x-a)2+(y-b)2=r2.
∵O、M1、M2三点在圆上,
∴它们的坐标满足方程
∴所求圆的方程为:(x-4)2+(y+3)2=52,
∴圆心坐标(4,-3),半径为r=5.
用一般式方程可以吗?
解此方程组,可得:a=-4,b=3,r2=25.
例1.求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求出这个圆的圆心坐标和半径.
另解:设所求的圆的方程为x2+y2+Dx+Ey+F=0(其中D2+E2-4F
>0).
∵O、M1、M2三点在圆上,
∴它们的坐标满足方程
即(x-4)2+(y+3)2=52,
∴圆心坐标(4,-3),半径为r=5.
与用标准式相比,有何特点?
解此方程组得:
D=-8,E=6,F=0.
∴所求圆的方程为:x2+y2-8x+6y=0.
思考:本题还有其它解法吗?
1.待定系数法:
(1)根据题意选择标准方程和一般方程;
若所给的条件与圆心和半径有直接关系,设为标准方程;
若条件主要是圆所经过的点的坐标,则宜用一般方程
(2)根据条件列出关于a,b,r或D,E,F的方程组。
(3)解出a,b,r或D,E,F,再求出圆方程。
2.数形结合:
结合图形,根据圆的性质相关求出圆心和半径,从而求出的方程
。
求圆方程的方法
练习
(1)方程x2+y2+Dx+Ey+F=0表示的曲线是以(-2,3)为圆心,4为半径的圆.求D、E、F的值
D=4,E=-6,F=-3
(
2)用待定系数法求出经过点A(1,-1)、B(1,4)、C(4,-2)的圆的方程.
x2+y2-7x-3y+2=0.
(
3)“求经过点A(4,-5),且与直线m:x-2y+4=0相切于点B(-2,1)的圆的方程”,有哪一些方法?
XJ
ZY
LX
例2.已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程
(x0,y0)
(x,y)
例析
.
O
x
y
.B(4,3)
.
.
M
A
解:
设点M为(x,y),点A为(x0,y0)
由中点坐标公式得
∴x0=2x-4,y0=2y-3,
即A(2x-4,2y-3)
∵A在圆(x+1)2+y2=4上
∴[(2x-4)+1]2+(2y-3)2=4,
∴线段AB的中点M的轨迹方程为
坐标代入法
(相关点法)
思考:这种方法的主要过程是怎样?
XJ
ZY
LX
例2.已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程
(x0,y0)
(x,y)
.
O
x
y
.B(4,3)
.
.
M
A
解:
设点M为(x,y),点A为(x0,y0)
由中点坐标公式得
∴x0=2x-4,y0=2y-3,
即A(2x-4,2y-3)
∵A在圆(x+1)2+y2=4上
∴[(2x-4)+1]2+(2y-3)2=4,
∴线段AB的中点M的轨迹方程为
归纳:
用坐标代入法
(相关点法)求方程的大致步骤:
(1)设出所求轨迹上任意一点和已知图形上相关点的坐标;(设坐标)
(2)根据条件用所求轨迹上任意一点的坐标将已知图形上点的坐标表示出来。(求坐标)
(3)将已知图形上点的坐标代入已知图形的方程并化简。(代入化简)
(4)
验证有无特殊情况
(验证)
XJ
ZY
LX
已知线段AB的端点B的坐标是(3,0),端点A在圆x2+y2=16上运动,P在直线AB上,且
求P的轨迹方程
(x0,y0)
(x,y)
练习
.
O
x
y
.
B(3,0)
.
.
P
A
解:
设点P为(x,y),点A为(x0,y0)
∴x0=9-2x,y0=2y
即A(9-2x,2y)
∵A在圆x2+y2=16上
∴(9-2x)2+(2y)2=16,
∴线段AB的中点M的轨迹方程为
XJ
ZY
LX
例3.经过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆
C于A、B两点,求线段AB的中点P的轨迹.
解:圆C的方程可化为(x-3)2+(y-2)2=4,其圆心为C(3,2),半径为2.
设P(x,y)是轨迹上任意一点.
∵CP⊥MP
∴当x≠3时,kCP?kMP=-1,即
化简得x2+y2+3x-2y-18=0,
经验证,当x=3时,此方程也成立
∴P的轨迹为圆x2+y2+3x-2y-18=0在圆C内部的一段圆弧.
直译法
思考:直译法的一般步骤是什么?
第一步,建系,设点;
第二步,找出点满足的几何条件;
第三步,将几何条件转化为代数条件;
第四步,化简;
第五步,验证有无特殊情况
.
XJ
ZY
LX
例析
已知点P到直线y+2=0和点F(1,1)点的距离相等;求证点P的轨迹是抛物线。
.
F(1,1)
(x,y)
练习
O
x
y
.
P
解:
设点P为(x,y),点P到m的距离为d
即
∴点M的轨迹为开口向上,对称轴为x=1的抛物线。
XJ
ZY
LX
由题意得,
y=-2
d=|PF|
练习
教材P123
练习
1,3题
XJ
ZY
P124
习题4.1
B组1,2
小结
一、
圆的方程:
1.标准方程:
(x?a)2
+
(y
?b)2
=
r2
特别地,
圆心在原点时,
x2
+y2
=
r2
2.圆的一般方程:
半径为:
圆心为:
圆心为:
(a,b)
半径为:
r
x2+y2+Dx+
Ey+F
=0(当D2+E2-4F>0时)
ZY
三、求圆方程的方法:
1.待定系数法:
(1)根据题意选择标准方程和一般方程;
若所给的条件与圆心和半径有直接关系,设为标准方程;
若条件主要是圆所经过的点的坐标,则宜用一般方程
(2)根据条件列出关于a,b,r或D,E,F的方程组。
(3)解出a,b,r或D,E,F,再求出圆方程。
2.数形结合:
结合图形,根据圆的性质求出圆心和半径,从而求出的方程时
。
ZY
四、用坐标代入法
(相关点法)求轨迹方程的主要步骤:
(1)设出所求轨迹上任意一点和已知图形上相关点的坐标;(建系设坐标)
(2)根据条件用所求轨迹上任意一点的坐标将已知图形上点的坐标表示出来。(求坐标)
(3)将已知图形上点的坐标代入已知图形的方程并化简。(代入化简)
(4)
验证有无特殊情况
(验证)
ZY
五、用直译法求轨迹方程的主要步骤:
(1)建立坐标系,设出该点坐标;
(2)找出点满足的几何条件;
(3)将几何条件转化为代数条件;
(4)将方程化简变形;
(5)验证有无特殊情况。
ZY
2.若圆C1:x2+y2=4和圆C2:x2+y2+4x-4y+4=0关于直线m对称。求直线
m的方程。
作业
1.已知圆过原点O(0,0)和点P(3,-1),且圆心在3x+y=5上,求此圆方程。
3.若P是圆O:x2+y2=4上一个动点,定点M为(4,4)。
(1)若OQ⊥QM,求点Q的轨迹的方程。
(2)若M始终是线段PQ的中点。求点Q的轨迹的方程。
