初中数学苏科版九年级上册3.4方差练习题(Word版 含解析)
文档属性
| 名称 | 初中数学苏科版九年级上册3.4方差练习题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 65.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 00:00:00 | ||
图片预览




文档简介
初中数学苏科版九年级上册第三章3.4方差练习题
一、选择题
某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是
A.
平均分不变,方差变大
B.
平均分不变,方差变小
C.
平均分和方差都不变
D.
平均分和方差都改变
如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数
185
180
185
180
方差
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择
A.
甲
B.
乙
C.
丙
D.
丁
图中信息是小明和小华射箭的成绩,两人都射了10箭,则射简成绩的方差较大的是
A.
小明
B.
小华
C.
两人一样
D.
无法确定
下列说法正确的是
A.
一个游戏的中奖概率是?则做10次这样的游戏一定会中奖
B.
为了解全国中学生的心理健康情况,应该采用普查的方式
C.
一组数据?8,8,7,10,6,8,9?的众数和中位数都是8
D.
若甲组数据的方差,乙组数据的方差,则乙组数据比甲组数据稳定
甲、乙、丙、丁四名学生近5次数学成绩的平均数都是110分,方差如表,则这四名学生成绩最稳定的是
学生
甲
乙
丙
丁
方差
A.
甲
B.
乙
C.
丙
D.
丁
甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好是环,方差分别是,,,,在本次射击测试中,成绩最稳定的是
A.
甲
B.
乙
C.
丙
D.
丁
在一次数学答题比赛中,五位同学答对题目的个数分别为7,5,3,5,10,则关于这组数据的说法不正确的是
A.
众数是5
B.
中位数是5
C.
平均数是6
D.
方差是
某班六名同学体能测试成绩分如下:80,90,75,75,80,80,对这组数据表述错误的是
A.
众数是80
B.
方差是25
C.
平均数是80
D.
中位数是75
一组数据:3,4,4,5,如果再添加一个数据4,那么会发生变化的统计量是
A.
平均数
B.
中位数
C.
众数
D.
方差
某特警部队为了选拔“神枪手”,举行了射击比赛,最后由甲、乙两名战士进入决赛,在相同条件下,两人各射靶10次,经过统计计算,甲、乙两名战士的总成绩都是99环,甲的方差是,乙的方差是,则下列说法中,正确的是
A.
甲的成绩比乙的成绩稳定
B.
甲、乙两人成绩的稳定性相同
C.
乙的成绩比甲的成绩稳定
D.
无法确定谁的成绩更稳定
二、填空题
已知一组数据a,b,c的方差为4,那么数据,,的方差是______.
某组数据,,0,1,2的方差为______.
若一组数据1,3,a,2,5的平均数是3,则______,这组数据的方差是______.
甲、乙两射击运动员的相同次数射击训练成绩的平均数和方差分别为,,,,则成绩较为稳定的运动员是______.
三、解答题
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上含为优秀.表是成绩最好的甲班和乙班5名学生的比赛数据单位:个:
1号
2号
3号
4号
5号
总数
甲班
89
100
96
118
97
500
乙班
100
95
110
91
104
500
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
计算两班的优秀率.
计算两班比赛数据的方差.
根据以上信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
为讴歌抗击新冠肺炎的白衣战士,某校在七年级中举行了“新时代最可爱的人”演讲比赛,七年级甲、乙两班分别选5名同学参加比赛,如图是根据其预赛成绩单位:分绘制的两幅不完整的统计图表,请你根据图表提供的信息完成以下问题:
项目
班级
平均数
中位数
众数
方差
甲班
85
______
85
70
乙班
______
80
______
160
填空:甲班2号选手的预赛成绩是______分,乙班3号选手的预赛成绩是______分,______班的预赛成绩更平衡,更稳定;
将上表中所缺的数据补充完整;
学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的区级比赛,求这5人预赛成绩的平均分数.
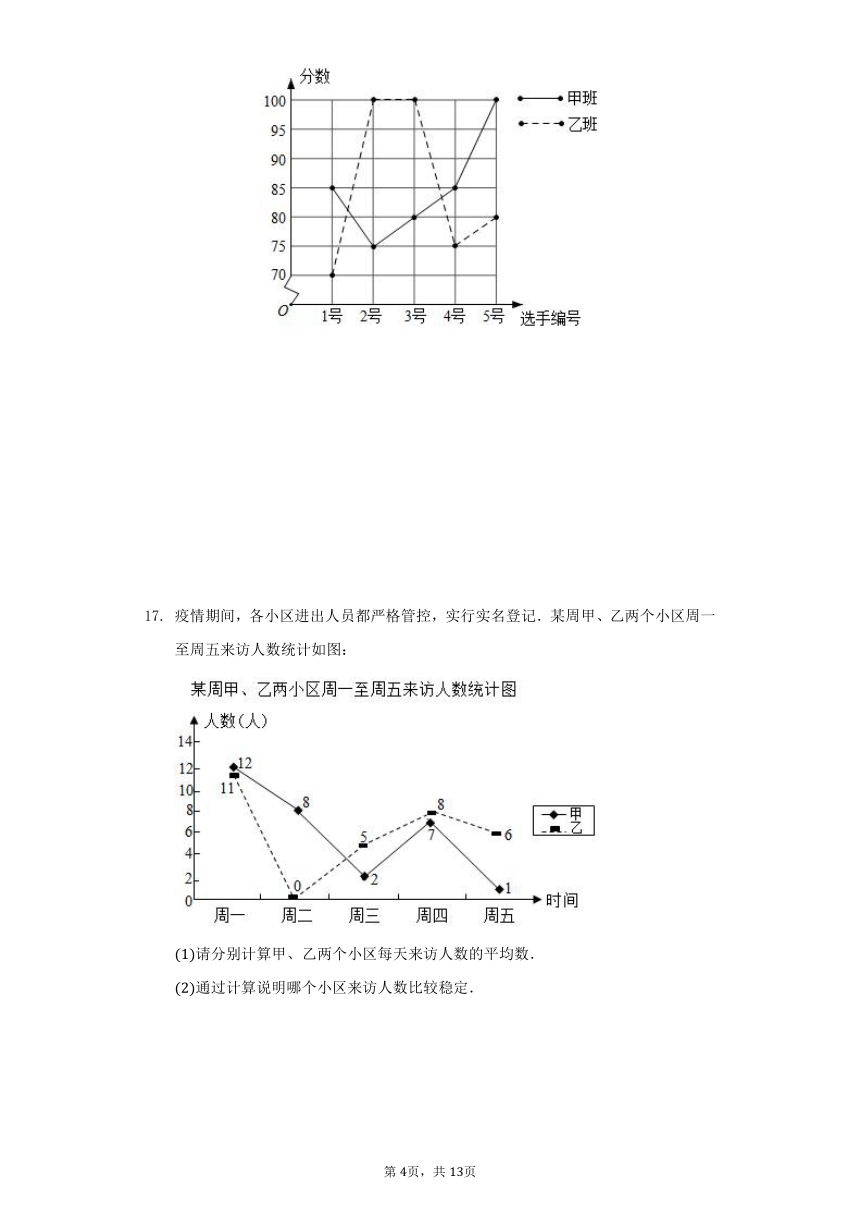
疫情期间,各小区进出人员都严格管控,实行实名登记.某周甲、乙两个小区周一至周五来访人数统计如图:
请分别计算甲、乙两个小区每天来访人数的平均数.
通过计算说明哪个小区来访人数比较稳定.
某班组织了“我和我的祖国”演讲比赛,甲,乙两队各有5人参加比赛,得分如下:分制
甲队
8
10
8
6
8
乙队
7
9
5
10
9
甲队成绩的众数是______分,乙队成绩的中位数是______分.
计算乙队成绩的平均数和方差.
已知甲队成绩的方差是,则成绩较为整齐的是哪个队?请根据甲队,乙队的方差比较得出结论.
答案和解析
1.【答案】B
【解析】解:小亮的成绩和其他39人的平均数相同,都是90分,
该班40人的测试成绩的平均分为90分,方差变小,
故选:B.
根据平均数,方差的定义计算即可.
本题考查方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
2.【答案】A
【解析】解:甲和丙的平均数大于乙和丁的平均数,
从甲和丙中选择一人参加比赛,
甲的方差小于丙的方差,
选择甲参赛,
故选:A.
首先比较平均数,平均数相同时选择方差较小的运动员参加.
此题考查了平均数和方差,正确理解方差与平均数的意义是解题关键.
3.【答案】B
【解析】解:根据图中的信息可知,小华的成绩波动性小,
故射箭成绩的方差较大的是小华
故选:B.
根据图中的信息找出波动性小的即可.
本题考查了方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
4.【答案】C
【解析】解:A、一个游戏的中奖概率是,则做10次这样的游戏可能中奖,故本选项错误;
B、了解全国中学生的心理健康情况,范围比较广,应采用抽查的反思调查,故本选项错误;
C、数据8,8,7,10,6,8,9中8出现的次数最多的为8,故众数为8,排序后中位数为8,故本选项正确;
D、根据方差越小越稳定可知乙组数据比甲组数据稳定,故本选项错误.
故选:C.
利用概率的意义、全面调查与抽样调查、中位数、众数及概率的意义逐项判断即可得到正确的答案.
本题考查了概率的意义、全面调查与抽样调查、中位数、众数及概率的意义,考查的知识点比较多,但相对比较简单.
5.【答案】D
【解析】解:由表可知丁的方差最小,
所以这四名学生成绩最稳定的是丁,
故选:D.
根据方差越小成绩越稳定求解可得.
本题主要考查方差,解题的关键是掌握方差的意义:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
6.【答案】C
【解析】解:
,
丙成绩最稳定,
故选:C.
根据方差是用来衡量一组数据波动大小的量,故由甲乙丙丁的方差可直接作出判断.
本题主要考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.【答案】D
【解析】解:A、数据中5出现2次,所以众数为5,此选项正确;
B、数据重新排列为3、5、5、7、10,则中位数为5,此选项正确;
C、平均数为,此选项正确;
D、方差为,此选项错误;
故选:D.
根据平均数、中位数、众数以及方差的定义判断各选项正误即可.
本题主要考查了方差、平均数、中位数以及众数的知识,解答本题的关键是熟练掌握各个知识点的定义以及计算公式,此题难度不大.
8.【答案】D
【解析】解:A、80出现的次数最多,所以众数是80,正确,不符合题意;
B、方差是:,正确,不符合题意;
C、平均数是,正确,不符合题意;
D、把数据按大小排列,中间两个数都为80,80,所以中位数是80,错误,符合题意.
故选:D.
根据众数,方差、平均数,中位数的概念逐项分析即可.
本题为统计题,考查方差、众数、平均数与中位数的意义.中位数是将一组数据从小到大或从大到小重新排列后,最中间的那个数或最中间两个数的平均数,叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
9.【答案】D
【解析】解:原数据的3,4,5,4的平均数为,中位数为4,众数为4,方差为;
新数据3,4,4,4,5的平均数为,中位数为4,众数为4,方差为;
故选:D.
依据的定义和公式分别计算新旧两组数据的平均数、中位数、众数、方差求解即可.
本题主要考查的是众数、中位数、方差、平均数,熟练掌握相关概念和公式是解题的关键.
10.【答案】C
【解析】解:甲的方差是,乙的方差是,
,
乙的成绩比甲的成绩稳定;
故选:C.
根据方差的定义,方差越小数据越稳定即可判断.
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
11.【答案】36
【解析】解:数据a,b,c的方差为4,
数据,,的方差,
故答案为:36.
根据“当数据都乘以一个数或除以一个数时,平均数也乘以或除以这个数,方差变为这个数的平方倍”求解可得.
本题考查了方差的定义.当数据都加上一个数或减去一个数时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数或除以一个数时,平均数也乘以或除以这个数,方差变为这个数的平方倍.
12.【答案】2
【解析】解:这组数据的平均数是:,
则数据的方差;
故答案为:2.
先由平均数的计算公式先求出这组数据的平均数,再根据方差公式进行计算即可.
本题考查了方差,一般地设n个数据,,,的平均数为,则方差
13.【答案】4
?
2
【解析】解:数据1,3,a,2,5的平均数是3,
,
则这组数据的方差是;
故答案为:4,2.
根据平均数的计算公式先求出a,再代入方差公式进行计算即可.
此题考查了平均数和方差的定义.平均数是所以数据的和除以所有数据的个数.方差的公式
14.【答案】甲
【解析】解:,,
,
成绩较为稳定的运动员是甲,
故答案为:甲.
方差越小成绩越稳定,据此可得答案.
本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
15.【答案】解:甲班的优秀率:,
乙班的优秀率:;
甲班的平均数个,
甲班的方差;
乙班的平均数个,
乙班的方差;
冠军奖杯应发给乙班.因为乙班5名学生的比赛成绩的优秀率比甲班高,方差比甲班小,综合评定乙班踢毽子水平较好.
【解析】根据优秀率的公式:优秀人数总人数,进行计算即可;
根据方程的计算公式,计算即可;
根据优秀率和方差进行比较即可.
本题考查了方差,以及优秀率的概念,并且运用它们的意义解决问题.
16.【答案】85?
85?
100?
75?
100?
甲
【解析】解:甲班2号选手的预赛成绩是75分,乙班3号选手的预赛成绩是100分,
由折线统计图知,甲班预赛成绩波动幅度小,
甲班的预赛成绩更平衡,更稳定;
故答案为:75,100,甲;
甲班成绩重新排列为75、80、85、85、100,
甲班成绩的中位数为85分;
乙班成绩重新排列为70、75、80、100、100,
乙班成绩的平均数为,众数为100,
补全表格如下:
项目
班级
平均数
中位数
众数
方差
甲班
85
85
85
70
乙班
85
80
100
160
学校选取的5名同学的预赛成绩为:100,100,100,85,85;
所以,他们的平均分数为:?分
答:这5名同学预赛成绩的平均分数为分.
结合折线统计图可得甲班2号选手成绩和乙班3号成绩,根据预赛成绩波动幅度的大小可判断成绩稳定性;
根据中位数、平均数和众数的概念求解可得;
根据平均数的定义计算出学校选取的5名同学的预赛成绩的平均数即可得.
此题考查了方差、平均数、众数和中位数,一般地设n个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
17.【答案】解:人,人,
甲、乙两个小区每天来访人数的平均数均为6人;
人,
人,
,
乙小区来访人数比较稳定.
【解析】利用算术平均数的定义列式计算可得;
计算出甲、乙小区来访人数的方差,根据方差的意义求解可得.
本题主要考查算术平均数和方差,解题的关键是掌握算术平均数和方差的定义及方差的意义.
18.【答案】8?
9
【解析】解:甲队成绩中8出现3次,次数最多,
甲队成绩的众数为8分,
乙队成绩重新排列为5、7、9、9、10,
乙队成绩的中位数是9分,
故答案为:8,9;
乙队成绩的平均数为分,
乙队成绩的方差为;
甲队成绩较为整齐,
,,
,
甲队成绩较为整齐.
根据众数和中位数的定义列式计算可得;
根据平均数和方差的定义求解可得;
将甲、乙的成绩的方差比较大小,再根据方差的意义求解可得.
考查中位数、众数、方差的计算方法,理解各个统计量的意义和计算方法是正确解答的关键.
第2页,共2页
第1页,共1页
一、选择题
某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是
A.
平均分不变,方差变大
B.
平均分不变,方差变小
C.
平均分和方差都不变
D.
平均分和方差都改变
如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数
185
180
185
180
方差
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择
A.
甲
B.
乙
C.
丙
D.
丁
图中信息是小明和小华射箭的成绩,两人都射了10箭,则射简成绩的方差较大的是
A.
小明
B.
小华
C.
两人一样
D.
无法确定
下列说法正确的是
A.
一个游戏的中奖概率是?则做10次这样的游戏一定会中奖
B.
为了解全国中学生的心理健康情况,应该采用普查的方式
C.
一组数据?8,8,7,10,6,8,9?的众数和中位数都是8
D.
若甲组数据的方差,乙组数据的方差,则乙组数据比甲组数据稳定
甲、乙、丙、丁四名学生近5次数学成绩的平均数都是110分,方差如表,则这四名学生成绩最稳定的是
学生
甲
乙
丙
丁
方差
A.
甲
B.
乙
C.
丙
D.
丁
甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好是环,方差分别是,,,,在本次射击测试中,成绩最稳定的是
A.
甲
B.
乙
C.
丙
D.
丁
在一次数学答题比赛中,五位同学答对题目的个数分别为7,5,3,5,10,则关于这组数据的说法不正确的是
A.
众数是5
B.
中位数是5
C.
平均数是6
D.
方差是
某班六名同学体能测试成绩分如下:80,90,75,75,80,80,对这组数据表述错误的是
A.
众数是80
B.
方差是25
C.
平均数是80
D.
中位数是75
一组数据:3,4,4,5,如果再添加一个数据4,那么会发生变化的统计量是
A.
平均数
B.
中位数
C.
众数
D.
方差
某特警部队为了选拔“神枪手”,举行了射击比赛,最后由甲、乙两名战士进入决赛,在相同条件下,两人各射靶10次,经过统计计算,甲、乙两名战士的总成绩都是99环,甲的方差是,乙的方差是,则下列说法中,正确的是
A.
甲的成绩比乙的成绩稳定
B.
甲、乙两人成绩的稳定性相同
C.
乙的成绩比甲的成绩稳定
D.
无法确定谁的成绩更稳定
二、填空题
已知一组数据a,b,c的方差为4,那么数据,,的方差是______.
某组数据,,0,1,2的方差为______.
若一组数据1,3,a,2,5的平均数是3,则______,这组数据的方差是______.
甲、乙两射击运动员的相同次数射击训练成绩的平均数和方差分别为,,,,则成绩较为稳定的运动员是______.
三、解答题
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上含为优秀.表是成绩最好的甲班和乙班5名学生的比赛数据单位:个:
1号
2号
3号
4号
5号
总数
甲班
89
100
96
118
97
500
乙班
100
95
110
91
104
500
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
计算两班的优秀率.
计算两班比赛数据的方差.
根据以上信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
为讴歌抗击新冠肺炎的白衣战士,某校在七年级中举行了“新时代最可爱的人”演讲比赛,七年级甲、乙两班分别选5名同学参加比赛,如图是根据其预赛成绩单位:分绘制的两幅不完整的统计图表,请你根据图表提供的信息完成以下问题:
项目
班级
平均数
中位数
众数
方差
甲班
85
______
85
70
乙班
______
80
______
160
填空:甲班2号选手的预赛成绩是______分,乙班3号选手的预赛成绩是______分,______班的预赛成绩更平衡,更稳定;
将上表中所缺的数据补充完整;
学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的区级比赛,求这5人预赛成绩的平均分数.
疫情期间,各小区进出人员都严格管控,实行实名登记.某周甲、乙两个小区周一至周五来访人数统计如图:
请分别计算甲、乙两个小区每天来访人数的平均数.
通过计算说明哪个小区来访人数比较稳定.
某班组织了“我和我的祖国”演讲比赛,甲,乙两队各有5人参加比赛,得分如下:分制
甲队
8
10
8
6
8
乙队
7
9
5
10
9
甲队成绩的众数是______分,乙队成绩的中位数是______分.
计算乙队成绩的平均数和方差.
已知甲队成绩的方差是,则成绩较为整齐的是哪个队?请根据甲队,乙队的方差比较得出结论.
答案和解析
1.【答案】B
【解析】解:小亮的成绩和其他39人的平均数相同,都是90分,
该班40人的测试成绩的平均分为90分,方差变小,
故选:B.
根据平均数,方差的定义计算即可.
本题考查方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
2.【答案】A
【解析】解:甲和丙的平均数大于乙和丁的平均数,
从甲和丙中选择一人参加比赛,
甲的方差小于丙的方差,
选择甲参赛,
故选:A.
首先比较平均数,平均数相同时选择方差较小的运动员参加.
此题考查了平均数和方差,正确理解方差与平均数的意义是解题关键.
3.【答案】B
【解析】解:根据图中的信息可知,小华的成绩波动性小,
故射箭成绩的方差较大的是小华
故选:B.
根据图中的信息找出波动性小的即可.
本题考查了方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
4.【答案】C
【解析】解:A、一个游戏的中奖概率是,则做10次这样的游戏可能中奖,故本选项错误;
B、了解全国中学生的心理健康情况,范围比较广,应采用抽查的反思调查,故本选项错误;
C、数据8,8,7,10,6,8,9中8出现的次数最多的为8,故众数为8,排序后中位数为8,故本选项正确;
D、根据方差越小越稳定可知乙组数据比甲组数据稳定,故本选项错误.
故选:C.
利用概率的意义、全面调查与抽样调查、中位数、众数及概率的意义逐项判断即可得到正确的答案.
本题考查了概率的意义、全面调查与抽样调查、中位数、众数及概率的意义,考查的知识点比较多,但相对比较简单.
5.【答案】D
【解析】解:由表可知丁的方差最小,
所以这四名学生成绩最稳定的是丁,
故选:D.
根据方差越小成绩越稳定求解可得.
本题主要考查方差,解题的关键是掌握方差的意义:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
6.【答案】C
【解析】解:
,
丙成绩最稳定,
故选:C.
根据方差是用来衡量一组数据波动大小的量,故由甲乙丙丁的方差可直接作出判断.
本题主要考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.【答案】D
【解析】解:A、数据中5出现2次,所以众数为5,此选项正确;
B、数据重新排列为3、5、5、7、10,则中位数为5,此选项正确;
C、平均数为,此选项正确;
D、方差为,此选项错误;
故选:D.
根据平均数、中位数、众数以及方差的定义判断各选项正误即可.
本题主要考查了方差、平均数、中位数以及众数的知识,解答本题的关键是熟练掌握各个知识点的定义以及计算公式,此题难度不大.
8.【答案】D
【解析】解:A、80出现的次数最多,所以众数是80,正确,不符合题意;
B、方差是:,正确,不符合题意;
C、平均数是,正确,不符合题意;
D、把数据按大小排列,中间两个数都为80,80,所以中位数是80,错误,符合题意.
故选:D.
根据众数,方差、平均数,中位数的概念逐项分析即可.
本题为统计题,考查方差、众数、平均数与中位数的意义.中位数是将一组数据从小到大或从大到小重新排列后,最中间的那个数或最中间两个数的平均数,叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
9.【答案】D
【解析】解:原数据的3,4,5,4的平均数为,中位数为4,众数为4,方差为;
新数据3,4,4,4,5的平均数为,中位数为4,众数为4,方差为;
故选:D.
依据的定义和公式分别计算新旧两组数据的平均数、中位数、众数、方差求解即可.
本题主要考查的是众数、中位数、方差、平均数,熟练掌握相关概念和公式是解题的关键.
10.【答案】C
【解析】解:甲的方差是,乙的方差是,
,
乙的成绩比甲的成绩稳定;
故选:C.
根据方差的定义,方差越小数据越稳定即可判断.
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
11.【答案】36
【解析】解:数据a,b,c的方差为4,
数据,,的方差,
故答案为:36.
根据“当数据都乘以一个数或除以一个数时,平均数也乘以或除以这个数,方差变为这个数的平方倍”求解可得.
本题考查了方差的定义.当数据都加上一个数或减去一个数时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数或除以一个数时,平均数也乘以或除以这个数,方差变为这个数的平方倍.
12.【答案】2
【解析】解:这组数据的平均数是:,
则数据的方差;
故答案为:2.
先由平均数的计算公式先求出这组数据的平均数,再根据方差公式进行计算即可.
本题考查了方差,一般地设n个数据,,,的平均数为,则方差
13.【答案】4
?
2
【解析】解:数据1,3,a,2,5的平均数是3,
,
则这组数据的方差是;
故答案为:4,2.
根据平均数的计算公式先求出a,再代入方差公式进行计算即可.
此题考查了平均数和方差的定义.平均数是所以数据的和除以所有数据的个数.方差的公式
14.【答案】甲
【解析】解:,,
,
成绩较为稳定的运动员是甲,
故答案为:甲.
方差越小成绩越稳定,据此可得答案.
本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
15.【答案】解:甲班的优秀率:,
乙班的优秀率:;
甲班的平均数个,
甲班的方差;
乙班的平均数个,
乙班的方差;
冠军奖杯应发给乙班.因为乙班5名学生的比赛成绩的优秀率比甲班高,方差比甲班小,综合评定乙班踢毽子水平较好.
【解析】根据优秀率的公式:优秀人数总人数,进行计算即可;
根据方程的计算公式,计算即可;
根据优秀率和方差进行比较即可.
本题考查了方差,以及优秀率的概念,并且运用它们的意义解决问题.
16.【答案】85?
85?
100?
75?
100?
甲
【解析】解:甲班2号选手的预赛成绩是75分,乙班3号选手的预赛成绩是100分,
由折线统计图知,甲班预赛成绩波动幅度小,
甲班的预赛成绩更平衡,更稳定;
故答案为:75,100,甲;
甲班成绩重新排列为75、80、85、85、100,
甲班成绩的中位数为85分;
乙班成绩重新排列为70、75、80、100、100,
乙班成绩的平均数为,众数为100,
补全表格如下:
项目
班级
平均数
中位数
众数
方差
甲班
85
85
85
70
乙班
85
80
100
160
学校选取的5名同学的预赛成绩为:100,100,100,85,85;
所以,他们的平均分数为:?分
答:这5名同学预赛成绩的平均分数为分.
结合折线统计图可得甲班2号选手成绩和乙班3号成绩,根据预赛成绩波动幅度的大小可判断成绩稳定性;
根据中位数、平均数和众数的概念求解可得;
根据平均数的定义计算出学校选取的5名同学的预赛成绩的平均数即可得.
此题考查了方差、平均数、众数和中位数,一般地设n个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
17.【答案】解:人,人,
甲、乙两个小区每天来访人数的平均数均为6人;
人,
人,
,
乙小区来访人数比较稳定.
【解析】利用算术平均数的定义列式计算可得;
计算出甲、乙小区来访人数的方差,根据方差的意义求解可得.
本题主要考查算术平均数和方差,解题的关键是掌握算术平均数和方差的定义及方差的意义.
18.【答案】8?
9
【解析】解:甲队成绩中8出现3次,次数最多,
甲队成绩的众数为8分,
乙队成绩重新排列为5、7、9、9、10,
乙队成绩的中位数是9分,
故答案为:8,9;
乙队成绩的平均数为分,
乙队成绩的方差为;
甲队成绩较为整齐,
,,
,
甲队成绩较为整齐.
根据众数和中位数的定义列式计算可得;
根据平均数和方差的定义求解可得;
将甲、乙的成绩的方差比较大小,再根据方差的意义求解可得.
考查中位数、众数、方差的计算方法,理解各个统计量的意义和计算方法是正确解答的关键.
第2页,共2页
第1页,共1页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
