【2012优化方案同步优化训练】人教B版 数学:必修3 第3章3.3.1
文档属性
| 名称 | 【2012优化方案同步优化训练】人教B版 数学:必修3 第3章3.3.1 |

|
|
| 格式 | zip | ||
| 文件大小 | 119.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-14 00:00:00 | ||
图片预览

文档简介
1.下面关于几何概型的说法错误的是( )
A.几何概型也是古典概型的一种
B.几何概型中事件发生的概率与位置、形状无关
C.几何概型在一次试验中可能出现的结果有无限个
D.几何概型中每个结果的发生具有等可能性
解析:选A.几何概型基本事件的个数是无限的,而古典概型要求基本事件有有限个,故几何概型不是古典概型,故选A.
2.某灯泡厂的一批灯泡的寿命均匀分布在区间[28,98]天内,从这批灯泡中任取一只寿命超过60天的概率是( )
A. B.
C. D.
解析:选D.P==.
3.在区间[1,3]上任取一数,则这个数大于等于1.5的概率为( )
A.0.25 B.0.5
C.0.6 D.0.75
答案:D
4.一个球形容器的半径为3 cm,里面装有纯净水,因不小心混入了1个感冒病毒,从中任取1 mL水,含有感冒病毒的概率为________.
解析:水的体积为πR3=π×33=36π(cm3)=36π(mL).则含有感冒病毒的概率P(A)=.
答案:
5.已知地铁列车每10 min一班,在车站停1 min,则乘客到达站台立即乘上车的概率是________.
解析:P==.
答案:
一、选择题
1.有一杯1 L的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1 L水,则小杯水中含有这个细菌的概率为( )
A.0 B.0.1
C.0.01 D.1
答案:B
2.一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒.当你到达路口时,看见红灯、黄灯与不看见红灯三种情况的概率依次是( )
A.、、 B.、、
C.、、 D.、、
答案:A
3.两根相距3 m的木杆上系了一根拉直的绳子,并在绳子上挂一彩珠,则彩珠与两端距离都大于1 m的概率为( )
A. B.
C. D.
答案:B
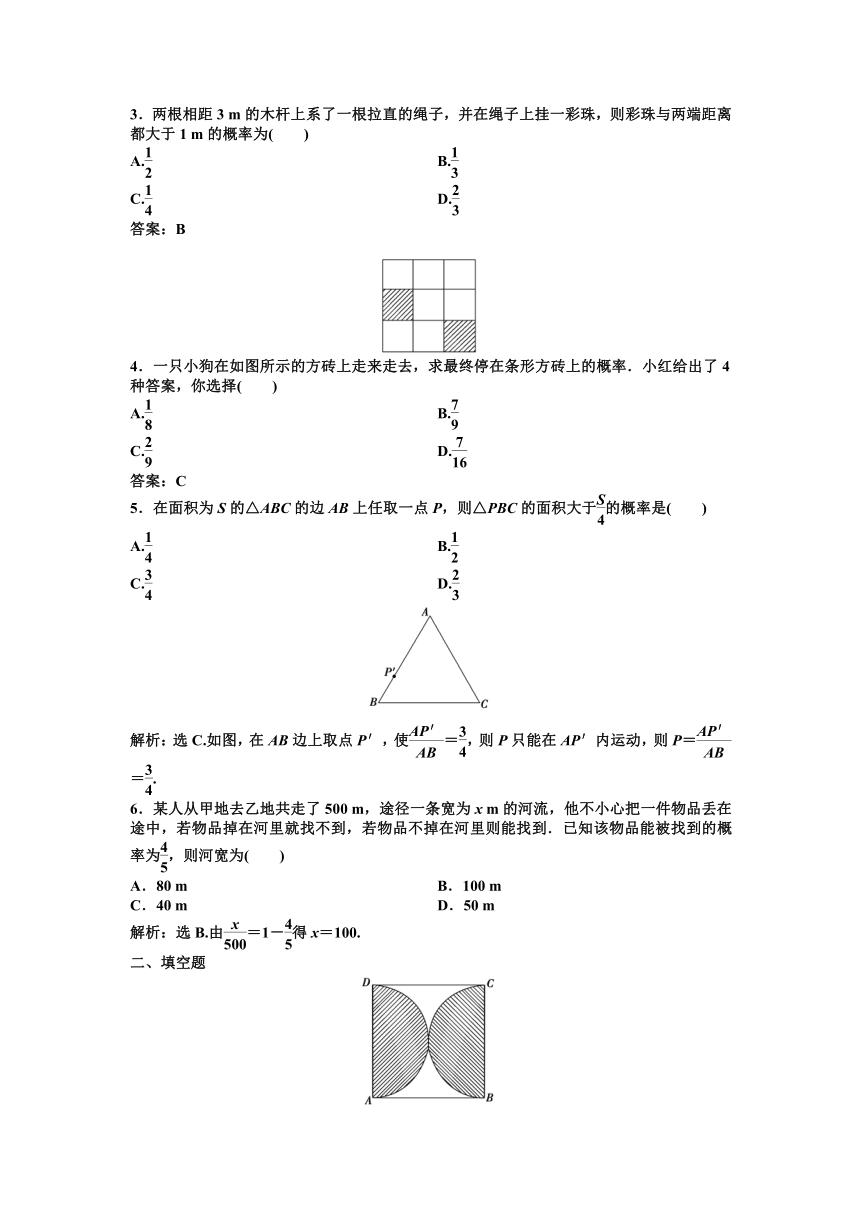
4.一只小狗在如图所示的方砖上走来走去,求最终停在条形方砖上的概率.小红给出了4种答案,你选择( )
A. B.
C. D.
答案:C
5.在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是( )
A. B.
C. D.
解析:选C.如图,在AB边上取点P′,使=,则P只能在AP′内运动,则P==.
6.某人从甲地去乙地共走了500 m,途径一条宽为x m的河流,他不小心把一件物品丢在途中,若物品掉在河里就找不到,若物品不掉在河里则能找到.已知该物品能被找到的概率为,则河宽为( )
A.80 m B.100 m
C.40 m D.50 m
解析:选B.由=1-得x=100.
二、填空题
7.如图,以正方形ABCD的左右两边为直径在正方形内部作半圆,现在向该正方形区域内随机地投掷一飞镖,则飞镖落在图中阴影部分的概率是________.
解析:依题意得这是个面积型的几何概型问题,由几何概型公式可知:P===.
答案:
8.甲、乙两人约定在6时到7时之间在某地会面,并约定先到者应等候另一个人一刻钟,过时即可离去.则两人能会面的概率是________.
解析:以x,y分别表示甲、乙两人到会面地点后的时间(如图所示),|x-y|≤15分钟的区域表示两人能会面(图中阴影部分).正方形内的点是随机发生的样本点,满足几何概型的特点,设A={能会面},∴P(A)=(SA为阴影部分面积,S为正方形面积).
即P(A)==.
答案:
9.在半径为1的圆上随机地取两点,连成一条弦,则其长度超过圆内接等边三角形的边长的概率为________.
解析:记事件A={弦长超过圆内接等边三角形的边长}.取圆内接等边△BCD的顶点B为弦的一个端点,当另一点在劣弧上时,|BE|>|BC|,而劣弧的弧长是圆周长的,所以由几何概型概率公式得:P(A)=.
答案:
三、解答题
10.向面积为6的△ABC内任投一点P,求△PBC的面积小于2的概率.
解:
如图所示,由于向△ABC内任投一点,点P落在△ABC内任一位置是等可能的,因而本题为几何概型问题.设DE∥BC,DE分别交AB,AC于D,E两点,且DE上任一点P与边BC构成的三角形的面积恰为2,要使△PBC的面积小于2,只要点P落在梯形BCED内任一点即可,设△ABC的高为h,DE到BC的距离为h′,BC长为a,则S△ABC=a·h=6,∴ah=12.令S△PBC=2=a·h′,∴ah′=4,∴h′=h,且DE=BC=a.设事件A为“向△ABC内任投一点P,使△PBC的面积小于2”,那么事件A的几何度量为S梯形BCED=(DE+BC)·h′=(a+a)·=ah.
该试验的全体基本事件的几何度量为S△ABC=ah.由几何概型的概率公式得P(A)==.
11.一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,求下列事件的概率:
(1)豆子落在红色区域;
(2)豆子落在黄色区域;
(3)豆子落在绿色区域;
(4)豆子落在红色或绿色区域.
解:这是几何概型问题,一颗豆子落在每一点的可能性都是一样,计算每个事件发生的概率,也就是先求出事件发生的区域,一共9个方块.
(1)P==;
(2)P==;
(3)P==;
(4)P===.
12.设A为圆周上一定点,在圆周上等可能的任取一点与A连结,求弦长超过半径的倍的概率.
解:
如图所示,在⊙O上有一定点A,任取一点B与A连结,则弦长超过半径的倍,即为∠AOB的度数大于90°,而小于270°.
记“弦长超过半径的倍”为事件C,则C表示的范围是∠AOB∈(90°,270°).
则由几何概型求概率的公式,得
P(C)==.
A.几何概型也是古典概型的一种
B.几何概型中事件发生的概率与位置、形状无关
C.几何概型在一次试验中可能出现的结果有无限个
D.几何概型中每个结果的发生具有等可能性
解析:选A.几何概型基本事件的个数是无限的,而古典概型要求基本事件有有限个,故几何概型不是古典概型,故选A.
2.某灯泡厂的一批灯泡的寿命均匀分布在区间[28,98]天内,从这批灯泡中任取一只寿命超过60天的概率是( )
A. B.
C. D.
解析:选D.P==.
3.在区间[1,3]上任取一数,则这个数大于等于1.5的概率为( )
A.0.25 B.0.5
C.0.6 D.0.75
答案:D
4.一个球形容器的半径为3 cm,里面装有纯净水,因不小心混入了1个感冒病毒,从中任取1 mL水,含有感冒病毒的概率为________.
解析:水的体积为πR3=π×33=36π(cm3)=36π(mL).则含有感冒病毒的概率P(A)=.
答案:
5.已知地铁列车每10 min一班,在车站停1 min,则乘客到达站台立即乘上车的概率是________.
解析:P==.
答案:
一、选择题
1.有一杯1 L的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1 L水,则小杯水中含有这个细菌的概率为( )
A.0 B.0.1
C.0.01 D.1
答案:B
2.一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒.当你到达路口时,看见红灯、黄灯与不看见红灯三种情况的概率依次是( )
A.、、 B.、、
C.、、 D.、、
答案:A
3.两根相距3 m的木杆上系了一根拉直的绳子,并在绳子上挂一彩珠,则彩珠与两端距离都大于1 m的概率为( )
A. B.
C. D.
答案:B
4.一只小狗在如图所示的方砖上走来走去,求最终停在条形方砖上的概率.小红给出了4种答案,你选择( )
A. B.
C. D.
答案:C
5.在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是( )
A. B.
C. D.
解析:选C.如图,在AB边上取点P′,使=,则P只能在AP′内运动,则P==.
6.某人从甲地去乙地共走了500 m,途径一条宽为x m的河流,他不小心把一件物品丢在途中,若物品掉在河里就找不到,若物品不掉在河里则能找到.已知该物品能被找到的概率为,则河宽为( )
A.80 m B.100 m
C.40 m D.50 m
解析:选B.由=1-得x=100.
二、填空题
7.如图,以正方形ABCD的左右两边为直径在正方形内部作半圆,现在向该正方形区域内随机地投掷一飞镖,则飞镖落在图中阴影部分的概率是________.
解析:依题意得这是个面积型的几何概型问题,由几何概型公式可知:P===.
答案:
8.甲、乙两人约定在6时到7时之间在某地会面,并约定先到者应等候另一个人一刻钟,过时即可离去.则两人能会面的概率是________.
解析:以x,y分别表示甲、乙两人到会面地点后的时间(如图所示),|x-y|≤15分钟的区域表示两人能会面(图中阴影部分).正方形内的点是随机发生的样本点,满足几何概型的特点,设A={能会面},∴P(A)=(SA为阴影部分面积,S为正方形面积).
即P(A)==.
答案:
9.在半径为1的圆上随机地取两点,连成一条弦,则其长度超过圆内接等边三角形的边长的概率为________.
解析:记事件A={弦长超过圆内接等边三角形的边长}.取圆内接等边△BCD的顶点B为弦的一个端点,当另一点在劣弧上时,|BE|>|BC|,而劣弧的弧长是圆周长的,所以由几何概型概率公式得:P(A)=.
答案:
三、解答题
10.向面积为6的△ABC内任投一点P,求△PBC的面积小于2的概率.
解:
如图所示,由于向△ABC内任投一点,点P落在△ABC内任一位置是等可能的,因而本题为几何概型问题.设DE∥BC,DE分别交AB,AC于D,E两点,且DE上任一点P与边BC构成的三角形的面积恰为2,要使△PBC的面积小于2,只要点P落在梯形BCED内任一点即可,设△ABC的高为h,DE到BC的距离为h′,BC长为a,则S△ABC=a·h=6,∴ah=12.令S△PBC=2=a·h′,∴ah′=4,∴h′=h,且DE=BC=a.设事件A为“向△ABC内任投一点P,使△PBC的面积小于2”,那么事件A的几何度量为S梯形BCED=(DE+BC)·h′=(a+a)·=ah.
该试验的全体基本事件的几何度量为S△ABC=ah.由几何概型的概率公式得P(A)==.
11.一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,求下列事件的概率:
(1)豆子落在红色区域;
(2)豆子落在黄色区域;
(3)豆子落在绿色区域;
(4)豆子落在红色或绿色区域.
解:这是几何概型问题,一颗豆子落在每一点的可能性都是一样,计算每个事件发生的概率,也就是先求出事件发生的区域,一共9个方块.
(1)P==;
(2)P==;
(3)P==;
(4)P===.
12.设A为圆周上一定点,在圆周上等可能的任取一点与A连结,求弦长超过半径的倍的概率.
解:
如图所示,在⊙O上有一定点A,任取一点B与A连结,则弦长超过半径的倍,即为∠AOB的度数大于90°,而小于270°.
记“弦长超过半径的倍”为事件C,则C表示的范围是∠AOB∈(90°,270°).
则由几何概型求概率的公式,得
P(C)==.
