【2012优化方案同步课件】人教B版 数学:必修3 第1章1.1.1
文档属性
| 名称 | 【2012优化方案同步课件】人教B版 数学:必修3 第1章1.1.1 |

|
|
| 格式 | rar | ||
| 文件大小 | 492.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-14 00:00:00 | ||
图片预览










文档简介
(共34张PPT)
第1章 算法的初步
课标领航
本章概述
算法就是解决问题的步骤,算法也是数学及其应用的重要组成部分,是计算机科学的基础,利用计算机解决问题要用算法,在日常生活中做任何事情也都有算法.
本章主要包括算法与程序框图,基本算法语句,中国古代数学中的算法案例.
本章重点是算法的概念和特征,算法、程序框图以及三种基本逻辑结构,算法基本语句,经典算法案例.
本章难点一是会用自然语言描述解决一类问题的算法;二是用程序框图表示算法的三种基本逻辑结构;三是将具体问题的程序框图转化为程序语言;四是代数学中算法案例的编程.
学法指导
1.通过具体实例,体会、感受算法思想,理解算法的特点.
2.结合对具体数学实例的分析,通过模仿、操作、探索,学习设计程序框图表达解决问题的过程.
§1.1 算法与程序框图
1.1.1 算法的概念
1.1.1 算
法
的
概
念
课堂互动讲练
知能优化训练
课前自主学案
学习目标
1.通过对具体问题解决过程与步骤的分析,体会算法是解决问题的“机械”程序,并能在有限步内完成及算法思想.
2.通过对具体问题解决过程的步骤的探索和研究,掌握算法步骤,了解算法与求解一个具体问题的方法的区别,明确算法的要求.
3.初步学会为解决某具体问题设计算法.
课前自主学案
初中学过的求解一元二次方程组时消元的方法有代入消元法和加减消元法.
温故夯基
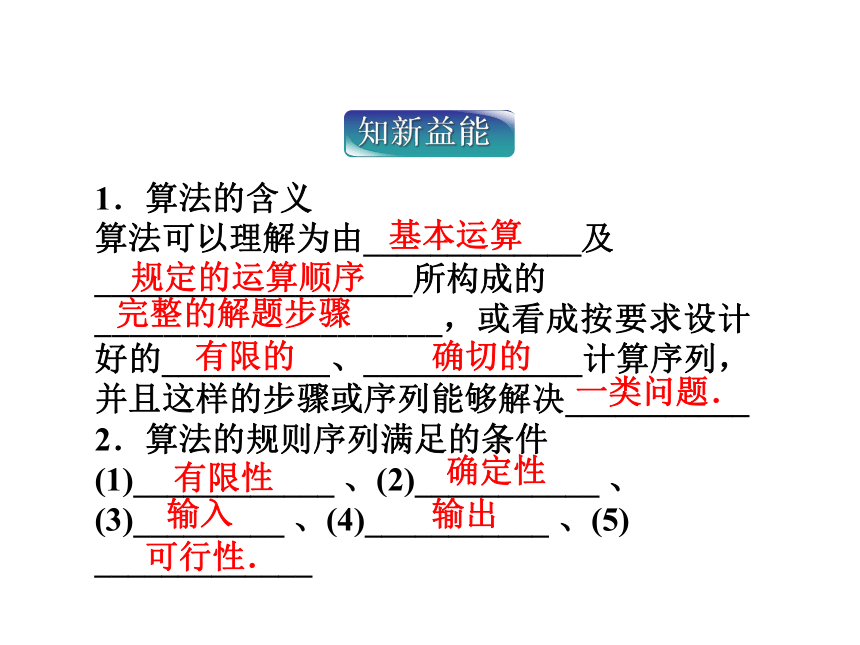
1.算法的含义
算法可以理解为由_____________及
___________________所构成的
____________________,或看成按要求设计好的__________、_____________计算序列,并且这样的步骤或序列能够解决___________
2.算法的规则序列满足的条件
(1)____________ 、(2)___________ 、
(3)_________ 、(4)___________ 、(5)
_____________
基本运算
规定的运算顺序
完整的解题步骤
有限的
确切的
一类问题.
有限性
确定性
输入
输出
可行性.
知新益能
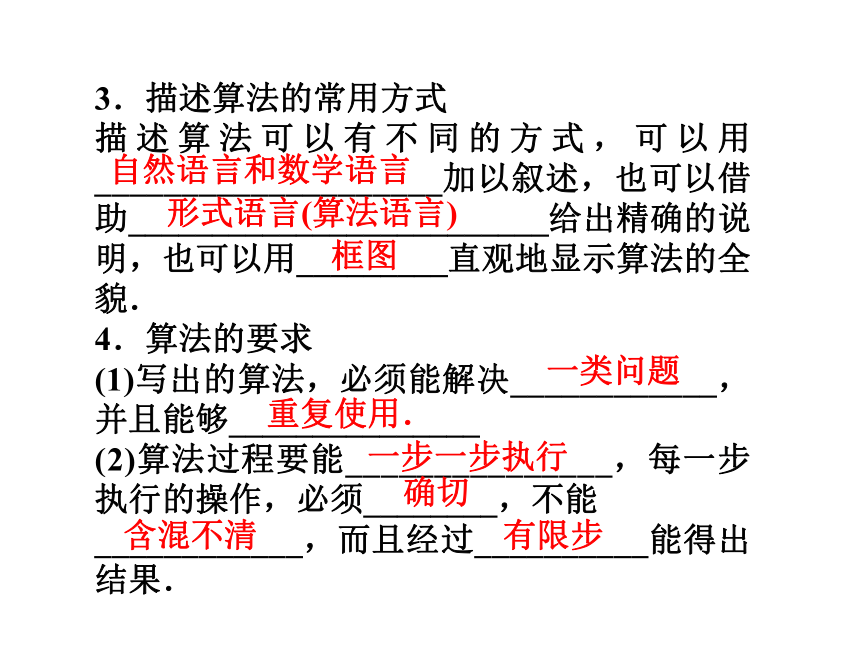
3.描述算法的常用方式
描述算法可以有不同的方式,可以用____________________加以叙述,也可以借助_________________________给出精确的说明,也可以用_________直观地显示算法的全貌.
4.算法的要求
(1)写出的算法,必须能解决____________,并且能够_______________
(2)算法过程要能_______________,每一步执行的操作,必须________,不能
____________,而且经过__________能得出结果.
自然语言和数学语言
形式语言(算法语言)
框图
一类问题
重复使用.
一步一步执行
确切
含混不清
有限步
思考感悟
算法与数学问题的解法有何区别和联系呢?
提示:(1)算法与解法是一般与特殊的关系,也是抽象与具体的关系,算法的获取要借助一般意义上具体问题的求解方法,而任何一个具体问题都可利用这类问题的一般方法解决.
(2)算法是解决某一问题所需要的程序和步骤的统称.也可以理解为数学中的“通法通解”,可以重复使用;而解法是解决某一个具体问题的过程和步骤,是具体的解题过程.
课堂互动讲练
算法的概念
考点突破
下列语句中是算法的有( )
①解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1;
②方程x2-1=0有两个实根;
③求1+2+3+4的值,先计算1+2=3,再由3+3=6,6+4=10得最终结果是10.
例1
A.1个 B.2个
C.3个 D.0个
【思路点拨】 由题目可获取以下主要信息:
①给出四个与算法有关的语句;
②判断各语句是否为算法语句.
解答本题可先正确理解算法的概念及其特点,然后逐一验证每个语句是否正确.
【解析】 ①中给出了一元一次方程这一类问题的解决方式;③中给出了求1+2+3+4的一个过程,最终得出结果;对于②,并没有说明如何去算,故①③是算法,②不是算法.
【答案】 B
【名师点评】 算法在中学课程中是一个新概念,算法实际上就是解决问题的一种程序性方法,它通常指向某一个或一类问题,而解决的过程是程序性和构造性的.算法又可以看成解决问题的特殊的有效方法,中学课程中的算法更强调具体算法所蕴涵的算法思想,重点在于培养学生的算法意识.
变式训练1 下列说法不正确的是( )
A.算法可以理解为由基本运算及规定的运算顺序构成的完整的解题步骤
B.算法可以看成按要求设计好的、有限的、明确的计算序列,并且这样的步骤或序列能够解决一类问题
C.算法只是在计算机产生之后才有的
D.描述算法有不同的方式,可以用日常语言和数学语言等
解析:选C.计算机只是解决算法的工具之一,生活中有些问题不是计算机能够求解的.
解方程(组)、不等式的算法
例2
【思路点拨】 由A1B2-A2B1≠0可知两个二元一次方程组表示的直线不平行且不重合,即两条直线必有一个交点也就是方程组必有一组解,可以用代入消元法或加减消元法解此方程组.
【解】 算法如下:
第一步:①×A2,得A1A2x+A2B1y+A2C1=0;③
第二步:②×A1,得A1A2x+A1B2y+A1C2=0;④
第三步:④-③,得(A1B2-A2B1)y+A1C2-A2C1=0;⑤
因此给出一个系数为常数的二元一次方程组,求它的解,除了根据本题的算法以外,还可以把它当作公式使用,就有了解二元一次方程组的公式法.在我们看来记忆非常麻烦,而作为计算机来讲只要有了相关的存储单元,将各系数输入就可直接输出方程组的解.
数值型问题的算法
写出计算S=1+2+3+4+6+…+100的算法.
【思路点拨】 i称作计数变量,每一次循环它的值增加1,由1变到100,S是一个累加变量,每一次循环得到一个新的结果,然后新的结果代替原值.
例3
【解】 第一步,令S=1;
第二步,令i=2;
第三步,使S+i的和变为S,即为S=S+i;
第四步,使i的值加1,即i=i+1;
第五步,若i≤100,则返回第三步,重新执行第三步、第四步、第五步,否则输出S,算法结束.
【名师点评】 对于有规律的数学问题(如累加、累乘等),我们可以通过归纳概括,由已知条件作为递推和迭代的基础,推出一般情况.
变式训练3 写出求1×3×5×7×9×11的值的一个算法.
解:S1 求1×3,得到结果3;
S2 将S1得到的乘积3再乘以5,得到结果15;
S3 将15再乘以7,得到105;
S4 将105再乘以9,得到945;
S5 将945再乘以11,得到10395.
任意给不等三个数a,b,c,设计一个算法,将a,b,c按从小到大的顺序排列出来.
【思路点拨】 只需将这三个数两两进行比较,并将最小的数赋给a,将最大的数赋给c,然后按a,b,c的顺序输出即可.
【解】 算法步骤为:
S1 输入三个数a,b,c;
S2 如果a>b,则将a,b两个数交换(t=a,a=b,b=t);否则转到下一步;(经过这一步,a储存的数就不超过b储存的数了)
非数值型计算问题的算法
例4
S3 如果a>c,则将a,c两个数交换(t=a,a=c,c=t);否则转到下一步;(此时a储存的数就不超过c储存的数了)
S4 如果b>c,则交换b,c两数(t=b,b=c,c=t);否则,转到下一步;(此时b储存的数就不超过c储存的数了)
S5 输出a,b,c.
【名师点评】 本例需三次比较,而每次比较时都引入第三个变量t,它只是起到“中转站”的作用,经过t把a,b中的数据进行交换,这个道理类似于用一盘空磁带把两盘内容不同的磁带A、B进行转录(交换磁带A、B的内容).
变式训练4 现在有三个油瓶,分别能装8 kg、5 kg、3 kg的油,当8 kg的瓶子装满时,设计一个用这三个瓶子倒油的算法,怎样倒能使这些油被平分到两个瓶子里.
解:S1 先规定8 kg的大油瓶为A、5 kg和3 kg的油瓶分别为B、C;
S2 从A往C倒3 kg,将C装满,此时A中剩下5 kg的油;
S3 将C中的3 kg油倒进B;
S4 再从A往C内倒3 kg的油;
S5 从C往B倒2 kg,即将B装满;
S6 将B中油全部倒入A;
S7 将C中油全部倒入B;
S8 从A往C倒油,将C装满,此时A中的油为4 kg;
S9 将C中油全部倒入B,则B中油也为4 kg.
1.正确理解算法的概念.一个程序的算法要本着方便、简洁的原则,还应讲究科学性,算法的步骤是按一定顺序进行的,不具有可逆性.
2.在设计算法的过程中要牢固把握住算法的五个特征:有限性、确定性、可行性、不唯一性、普遍性.
方法感悟
3.给出一个问题,设计算法时应注意:
(1)认真分析问题,联系解决此问题的一般方法;
(2)综合考虑此类问题的所有可能涉及的情况;
(3)将解决问题的过程分为若干个步骤;
(4)用简炼语言将各个步骤表示出来.
4.设计数值型问题算法时,如果有公式可用,应尽量应用公式来设计算法,如果有数学结论可用,应尽量应用数学结论来设计算法.
5.对于非数值型问题,在设计算法时,应当先建立过程模型,再把它细化为具体步骤即可.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
第1章 算法的初步
课标领航
本章概述
算法就是解决问题的步骤,算法也是数学及其应用的重要组成部分,是计算机科学的基础,利用计算机解决问题要用算法,在日常生活中做任何事情也都有算法.
本章主要包括算法与程序框图,基本算法语句,中国古代数学中的算法案例.
本章重点是算法的概念和特征,算法、程序框图以及三种基本逻辑结构,算法基本语句,经典算法案例.
本章难点一是会用自然语言描述解决一类问题的算法;二是用程序框图表示算法的三种基本逻辑结构;三是将具体问题的程序框图转化为程序语言;四是代数学中算法案例的编程.
学法指导
1.通过具体实例,体会、感受算法思想,理解算法的特点.
2.结合对具体数学实例的分析,通过模仿、操作、探索,学习设计程序框图表达解决问题的过程.
§1.1 算法与程序框图
1.1.1 算法的概念
1.1.1 算
法
的
概
念
课堂互动讲练
知能优化训练
课前自主学案
学习目标
1.通过对具体问题解决过程与步骤的分析,体会算法是解决问题的“机械”程序,并能在有限步内完成及算法思想.
2.通过对具体问题解决过程的步骤的探索和研究,掌握算法步骤,了解算法与求解一个具体问题的方法的区别,明确算法的要求.
3.初步学会为解决某具体问题设计算法.
课前自主学案
初中学过的求解一元二次方程组时消元的方法有代入消元法和加减消元法.
温故夯基
1.算法的含义
算法可以理解为由_____________及
___________________所构成的
____________________,或看成按要求设计好的__________、_____________计算序列,并且这样的步骤或序列能够解决___________
2.算法的规则序列满足的条件
(1)____________ 、(2)___________ 、
(3)_________ 、(4)___________ 、(5)
_____________
基本运算
规定的运算顺序
完整的解题步骤
有限的
确切的
一类问题.
有限性
确定性
输入
输出
可行性.
知新益能
3.描述算法的常用方式
描述算法可以有不同的方式,可以用____________________加以叙述,也可以借助_________________________给出精确的说明,也可以用_________直观地显示算法的全貌.
4.算法的要求
(1)写出的算法,必须能解决____________,并且能够_______________
(2)算法过程要能_______________,每一步执行的操作,必须________,不能
____________,而且经过__________能得出结果.
自然语言和数学语言
形式语言(算法语言)
框图
一类问题
重复使用.
一步一步执行
确切
含混不清
有限步
思考感悟
算法与数学问题的解法有何区别和联系呢?
提示:(1)算法与解法是一般与特殊的关系,也是抽象与具体的关系,算法的获取要借助一般意义上具体问题的求解方法,而任何一个具体问题都可利用这类问题的一般方法解决.
(2)算法是解决某一问题所需要的程序和步骤的统称.也可以理解为数学中的“通法通解”,可以重复使用;而解法是解决某一个具体问题的过程和步骤,是具体的解题过程.
课堂互动讲练
算法的概念
考点突破
下列语句中是算法的有( )
①解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1;
②方程x2-1=0有两个实根;
③求1+2+3+4的值,先计算1+2=3,再由3+3=6,6+4=10得最终结果是10.
例1
A.1个 B.2个
C.3个 D.0个
【思路点拨】 由题目可获取以下主要信息:
①给出四个与算法有关的语句;
②判断各语句是否为算法语句.
解答本题可先正确理解算法的概念及其特点,然后逐一验证每个语句是否正确.
【解析】 ①中给出了一元一次方程这一类问题的解决方式;③中给出了求1+2+3+4的一个过程,最终得出结果;对于②,并没有说明如何去算,故①③是算法,②不是算法.
【答案】 B
【名师点评】 算法在中学课程中是一个新概念,算法实际上就是解决问题的一种程序性方法,它通常指向某一个或一类问题,而解决的过程是程序性和构造性的.算法又可以看成解决问题的特殊的有效方法,中学课程中的算法更强调具体算法所蕴涵的算法思想,重点在于培养学生的算法意识.
变式训练1 下列说法不正确的是( )
A.算法可以理解为由基本运算及规定的运算顺序构成的完整的解题步骤
B.算法可以看成按要求设计好的、有限的、明确的计算序列,并且这样的步骤或序列能够解决一类问题
C.算法只是在计算机产生之后才有的
D.描述算法有不同的方式,可以用日常语言和数学语言等
解析:选C.计算机只是解决算法的工具之一,生活中有些问题不是计算机能够求解的.
解方程(组)、不等式的算法
例2
【思路点拨】 由A1B2-A2B1≠0可知两个二元一次方程组表示的直线不平行且不重合,即两条直线必有一个交点也就是方程组必有一组解,可以用代入消元法或加减消元法解此方程组.
【解】 算法如下:
第一步:①×A2,得A1A2x+A2B1y+A2C1=0;③
第二步:②×A1,得A1A2x+A1B2y+A1C2=0;④
第三步:④-③,得(A1B2-A2B1)y+A1C2-A2C1=0;⑤
因此给出一个系数为常数的二元一次方程组,求它的解,除了根据本题的算法以外,还可以把它当作公式使用,就有了解二元一次方程组的公式法.在我们看来记忆非常麻烦,而作为计算机来讲只要有了相关的存储单元,将各系数输入就可直接输出方程组的解.
数值型问题的算法
写出计算S=1+2+3+4+6+…+100的算法.
【思路点拨】 i称作计数变量,每一次循环它的值增加1,由1变到100,S是一个累加变量,每一次循环得到一个新的结果,然后新的结果代替原值.
例3
【解】 第一步,令S=1;
第二步,令i=2;
第三步,使S+i的和变为S,即为S=S+i;
第四步,使i的值加1,即i=i+1;
第五步,若i≤100,则返回第三步,重新执行第三步、第四步、第五步,否则输出S,算法结束.
【名师点评】 对于有规律的数学问题(如累加、累乘等),我们可以通过归纳概括,由已知条件作为递推和迭代的基础,推出一般情况.
变式训练3 写出求1×3×5×7×9×11的值的一个算法.
解:S1 求1×3,得到结果3;
S2 将S1得到的乘积3再乘以5,得到结果15;
S3 将15再乘以7,得到105;
S4 将105再乘以9,得到945;
S5 将945再乘以11,得到10395.
任意给不等三个数a,b,c,设计一个算法,将a,b,c按从小到大的顺序排列出来.
【思路点拨】 只需将这三个数两两进行比较,并将最小的数赋给a,将最大的数赋给c,然后按a,b,c的顺序输出即可.
【解】 算法步骤为:
S1 输入三个数a,b,c;
S2 如果a>b,则将a,b两个数交换(t=a,a=b,b=t);否则转到下一步;(经过这一步,a储存的数就不超过b储存的数了)
非数值型计算问题的算法
例4
S3 如果a>c,则将a,c两个数交换(t=a,a=c,c=t);否则转到下一步;(此时a储存的数就不超过c储存的数了)
S4 如果b>c,则交换b,c两数(t=b,b=c,c=t);否则,转到下一步;(此时b储存的数就不超过c储存的数了)
S5 输出a,b,c.
【名师点评】 本例需三次比较,而每次比较时都引入第三个变量t,它只是起到“中转站”的作用,经过t把a,b中的数据进行交换,这个道理类似于用一盘空磁带把两盘内容不同的磁带A、B进行转录(交换磁带A、B的内容).
变式训练4 现在有三个油瓶,分别能装8 kg、5 kg、3 kg的油,当8 kg的瓶子装满时,设计一个用这三个瓶子倒油的算法,怎样倒能使这些油被平分到两个瓶子里.
解:S1 先规定8 kg的大油瓶为A、5 kg和3 kg的油瓶分别为B、C;
S2 从A往C倒3 kg,将C装满,此时A中剩下5 kg的油;
S3 将C中的3 kg油倒进B;
S4 再从A往C内倒3 kg的油;
S5 从C往B倒2 kg,即将B装满;
S6 将B中油全部倒入A;
S7 将C中油全部倒入B;
S8 从A往C倒油,将C装满,此时A中的油为4 kg;
S9 将C中油全部倒入B,则B中油也为4 kg.
1.正确理解算法的概念.一个程序的算法要本着方便、简洁的原则,还应讲究科学性,算法的步骤是按一定顺序进行的,不具有可逆性.
2.在设计算法的过程中要牢固把握住算法的五个特征:有限性、确定性、可行性、不唯一性、普遍性.
方法感悟
3.给出一个问题,设计算法时应注意:
(1)认真分析问题,联系解决此问题的一般方法;
(2)综合考虑此类问题的所有可能涉及的情况;
(3)将解决问题的过程分为若干个步骤;
(4)用简炼语言将各个步骤表示出来.
4.设计数值型问题算法时,如果有公式可用,应尽量应用公式来设计算法,如果有数学结论可用,应尽量应用数学结论来设计算法.
5.对于非数值型问题,在设计算法时,应当先建立过程模型,再把它细化为具体步骤即可.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
