【2012优化方案同步课件】人教B版 数学:必修3 第1章1.1.3
文档属性
| 名称 | 【2012优化方案同步课件】人教B版 数学:必修3 第1章1.1.3 |

|
|
| 格式 | rar | ||
| 文件大小 | 741.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-14 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
1.1.3 算法的三种基本逻辑结构和框图表示
1.1.3 算法的三种基本逻辑结构和框图表示
课堂互动讲练
知能优化训练
课前自主学案
学习目标
1.在具体问题的解决过程中,理解程序框图的三种基本逻辑结构.
2.能正确选择并运用三种逻辑结构框图表示具体问题的算法.
3.通过训练,在问题解决的过程中,弄清三种基本结构的共同特点及每种结构的各自特点.
4.遇到具体问题要认真分析,选择合适的框图来描述算法.
课前自主学案
程序框图:由一些________________构成一张图来表示算法.
温故夯基
通用图形符号
1.顺序结构描述的是最简单的算法结构,_____________之间,____________之间按____________的顺序进行,它由若干个依次执行的处理步骤组成,它也是任何一个算法都离不开的一种算法结构.
2.条件分支结构是指依据___________选择执行不同指令的控制结构.
注意:条件分支结构的语句与语句之间,框与框之间必须有一个环节是概括条件进行判断的操作.
知新益能
语句与语句
框与框
从上到下
指定条件
思考感悟
1.条件分支结构中的判断框有两个出口,由此说明条件分支结构执行的结果,也就有两种可能,对吗?
提示:不对,判断框虽然有两个出口,但根据条件是否成立,选择的出口是确定的,故执行结果也是唯一的.
3.循环结构是指根据指定条件决定是否重复执行___________________的控制结构称为循环结构.即从算法某处开始,按照一定条件重复执行某一处理过程.
思考感悟
2.循环结构一定包含条件分支结构吗?
提示:在循环结构中需要判断是否继续循环,因此,循环结构一定包含条件分支结构.
一条或多条指令
课堂互动讲练
顺序结构的程序框图
考点突破
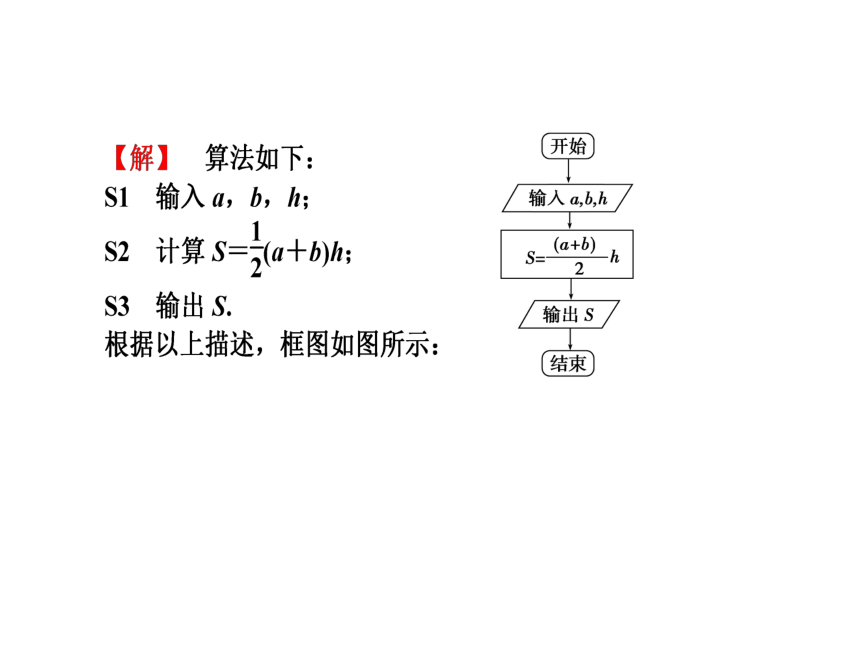
已知由梯形两底a,b和高h,设计一个求梯形面积的算法,并画出框图.
【思路点拨】 由题目可获取以下主要信息:①已知梯形两底a,b及高h;②设计求梯形面积的算法;③画出框图.解答本题可先根据题意确定算法步骤,并结合其算法类型选择顺序结构.
例1
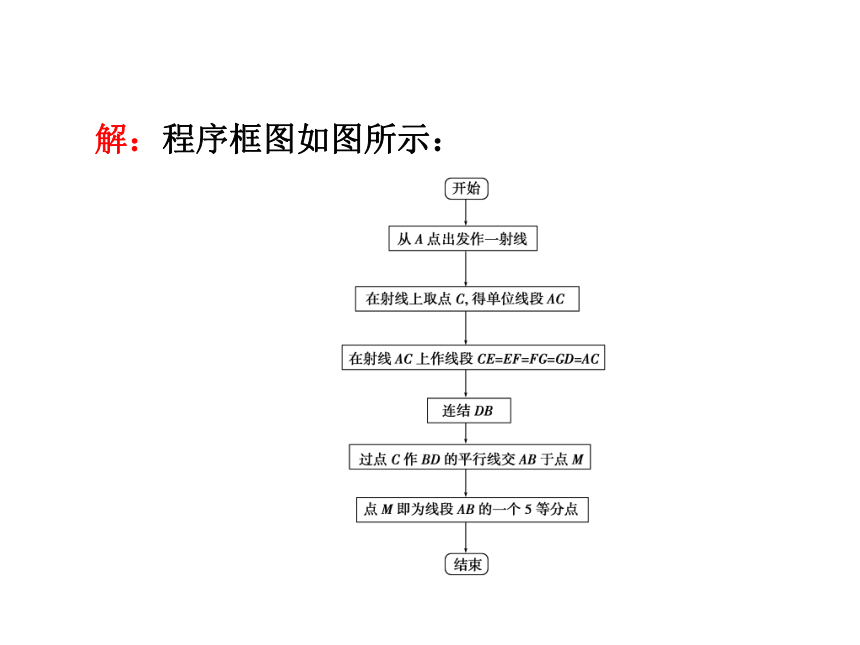
变式训练1 用尺规作图,确定线段AB的一个5等分点,写出解决这一问题的程序框图.
解:程序框图如图所示:
条件分支结构的程序框图
例2
【思路点拨】 该函数是分段函数,当x取不同范围内的值时,函数表达式不同,因此当给出一个自变量x的值时,必须先判断x的范围,然后确定利用哪一段的解析式求对应的函数值.因为解析式分了三段,所以判断框需要两个,即进行两次判断.
【解】 算法如下:
S1 输入x.
S2 如果x>0,则使y=-x+1,并转到S4;否则执行S3.
S3 如果x=0,则使y=0;否则y=x+3.
S4 输出y.
程序框图如图:
【名师点评】 求分段函数的函数值的程序框图的画法:如果是分两段的函数,只需引入一个判断框,如果分三段,则引入两个判断框,以此类推.
变式训练2 某居民区的物业管理部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出一人加收1.2元.设计一个算法,根据住户的人数,计算应收取的卫生费,并画出程序框图.
用循环结构程序框图解决累加、累乘问题
例3
画出计算12+22+32+…+992+1002的值的程序框图.
【思路点拨】 本题需一个累加变量和一个计数变量,将累加变量的初始值设为0,计数变量的值可以从1~100,因此可用循环结构描述算法.
【解】 如图所示.
【名师点评】 本题是典型
的累加问题,设计的关键是
把握好循环结构的三要素,
注意判断框内的条件.
变式训练3 试画出计算13×23×33×…×1003的算
法的一个框图.
解:算法的框图如图所示:
确定循环变量的最值的框图
写出一个求1×3×5×7×…×i>5000的最小正整数i的算法,并画出相应的程序框图.
【思路点拨】 本题应选择循环结构.
例4
【解】 算法如下:
S1 S=1;
S2 i=3;
S3 如果S≤5000,那么
S=S×i,i=i+2,重复
S3,否则,执行S4;
S4 i=i-2;
S5 输出i.
程序框图如图所示.
【名师点评】 对具有规
律性的重复计算,常用循
环结构.
实际应用
获得学习优良奖的条件如下:
(1)所考五门课成绩总分不低于450分;
(2)前三门(主课)每门成绩都在95分及其以上,其他两门(非主课)每门成绩在88分及其以上.
输入一名学生的五门课的成绩,问他是否符合优良条件,设计算法,并画出这一算法的程序框图.
例5
【思路点拨】 上述两个条件必须同时成立,这个学生才符合获得学习优良奖的条件.因此我们对每一个条件都进行判断.
【解】 设这名学生的五门课成绩分别为a,b,c,d,e,设计算法如下:
S1 输入学生五门课的成绩a,b,c,d,e;
S2 计算学生的总成绩S=a+b+c+d+e;
S3 若S≥450,则执行S4,否则执行S10;
S4 若a≥95,则执行S5,否则执行S10;
S5 若b≥95,则执行S6,否则执行S10;
S6 若c≥95,则执行S7,否则执行S10;
S7 若d≥88,则执行S8,否则执行S10;
S8 若e≥88,则执行S9,否则执行S10;
S9 输出“该学生获得学
习优良奖”;
S10 输出“该学生没获
得学习优良奖”.
根据上述算法,其程序框
图如图所示:
【名师点评】 本例是条件分支结构的实际应用,解题的关键是找出所有的判断条件.
变式训练4 某高中男子体育小组的50 m成绩(单位:s)如下:6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5,设计一个算法,从这些成绩中搜索小于6.8 s的成绩,并画出程序框图.
解:算法步骤如下:
S1 i=1;
S2 输入一个数据a;
S3 如果a<6.8,则输出a,
否则不输出,执行S4;
S4 i=i+1;
S5 如果i≤9,则执行S2;
否则结束算法.
程序框图如图所示.
1.程序框图包括顺序结构、条件分支结构和循环结构三种,正确画出算法的程序框图应建立在对算法透彻分析的基础上.
2.仔细审题,在画出程序框图时首先应进行结构的选择,套用公式,若求只含有一个关系式的解析式的函数值时,只用顺序结构就能解决;若是分段函数或被执行时需先判断后才能执行后继步骤的,就必需引入条件分支结构;
方法感悟
如果问题中涉及的运算进行了许多重复的步骤,且数之间有相同的规律,则可引入变量,应用循环结构,当然循环结构中一定用到顺序结构和条件分支结构.
3.具体绘制程序框图时,应注意以下几点:
(1)流程线上要有标志执行顺序的箭头;
(2)判断框后边的流程线应根据情况标注“是”或“否”;
(3)框图内的内容包括累计变量初始值、代数变量初始值、累加值,前后两个变量的差值都要仔细斟酌,不可有丝毫差错;
(4)判断框内内容的填写,有时大于等于,有时大于,有时小于,有时小于等于.它们的含义各不相同,应根据所选循环的类型,正确进行选择.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
1.1.3 算法的三种基本逻辑结构和框图表示
1.1.3 算法的三种基本逻辑结构和框图表示
课堂互动讲练
知能优化训练
课前自主学案
学习目标
1.在具体问题的解决过程中,理解程序框图的三种基本逻辑结构.
2.能正确选择并运用三种逻辑结构框图表示具体问题的算法.
3.通过训练,在问题解决的过程中,弄清三种基本结构的共同特点及每种结构的各自特点.
4.遇到具体问题要认真分析,选择合适的框图来描述算法.
课前自主学案
程序框图:由一些________________构成一张图来表示算法.
温故夯基
通用图形符号
1.顺序结构描述的是最简单的算法结构,_____________之间,____________之间按____________的顺序进行,它由若干个依次执行的处理步骤组成,它也是任何一个算法都离不开的一种算法结构.
2.条件分支结构是指依据___________选择执行不同指令的控制结构.
注意:条件分支结构的语句与语句之间,框与框之间必须有一个环节是概括条件进行判断的操作.
知新益能
语句与语句
框与框
从上到下
指定条件
思考感悟
1.条件分支结构中的判断框有两个出口,由此说明条件分支结构执行的结果,也就有两种可能,对吗?
提示:不对,判断框虽然有两个出口,但根据条件是否成立,选择的出口是确定的,故执行结果也是唯一的.
3.循环结构是指根据指定条件决定是否重复执行___________________的控制结构称为循环结构.即从算法某处开始,按照一定条件重复执行某一处理过程.
思考感悟
2.循环结构一定包含条件分支结构吗?
提示:在循环结构中需要判断是否继续循环,因此,循环结构一定包含条件分支结构.
一条或多条指令
课堂互动讲练
顺序结构的程序框图
考点突破
已知由梯形两底a,b和高h,设计一个求梯形面积的算法,并画出框图.
【思路点拨】 由题目可获取以下主要信息:①已知梯形两底a,b及高h;②设计求梯形面积的算法;③画出框图.解答本题可先根据题意确定算法步骤,并结合其算法类型选择顺序结构.
例1
变式训练1 用尺规作图,确定线段AB的一个5等分点,写出解决这一问题的程序框图.
解:程序框图如图所示:
条件分支结构的程序框图
例2
【思路点拨】 该函数是分段函数,当x取不同范围内的值时,函数表达式不同,因此当给出一个自变量x的值时,必须先判断x的范围,然后确定利用哪一段的解析式求对应的函数值.因为解析式分了三段,所以判断框需要两个,即进行两次判断.
【解】 算法如下:
S1 输入x.
S2 如果x>0,则使y=-x+1,并转到S4;否则执行S3.
S3 如果x=0,则使y=0;否则y=x+3.
S4 输出y.
程序框图如图:
【名师点评】 求分段函数的函数值的程序框图的画法:如果是分两段的函数,只需引入一个判断框,如果分三段,则引入两个判断框,以此类推.
变式训练2 某居民区的物业管理部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出一人加收1.2元.设计一个算法,根据住户的人数,计算应收取的卫生费,并画出程序框图.
用循环结构程序框图解决累加、累乘问题
例3
画出计算12+22+32+…+992+1002的值的程序框图.
【思路点拨】 本题需一个累加变量和一个计数变量,将累加变量的初始值设为0,计数变量的值可以从1~100,因此可用循环结构描述算法.
【解】 如图所示.
【名师点评】 本题是典型
的累加问题,设计的关键是
把握好循环结构的三要素,
注意判断框内的条件.
变式训练3 试画出计算13×23×33×…×1003的算
法的一个框图.
解:算法的框图如图所示:
确定循环变量的最值的框图
写出一个求1×3×5×7×…×i>5000的最小正整数i的算法,并画出相应的程序框图.
【思路点拨】 本题应选择循环结构.
例4
【解】 算法如下:
S1 S=1;
S2 i=3;
S3 如果S≤5000,那么
S=S×i,i=i+2,重复
S3,否则,执行S4;
S4 i=i-2;
S5 输出i.
程序框图如图所示.
【名师点评】 对具有规
律性的重复计算,常用循
环结构.
实际应用
获得学习优良奖的条件如下:
(1)所考五门课成绩总分不低于450分;
(2)前三门(主课)每门成绩都在95分及其以上,其他两门(非主课)每门成绩在88分及其以上.
输入一名学生的五门课的成绩,问他是否符合优良条件,设计算法,并画出这一算法的程序框图.
例5
【思路点拨】 上述两个条件必须同时成立,这个学生才符合获得学习优良奖的条件.因此我们对每一个条件都进行判断.
【解】 设这名学生的五门课成绩分别为a,b,c,d,e,设计算法如下:
S1 输入学生五门课的成绩a,b,c,d,e;
S2 计算学生的总成绩S=a+b+c+d+e;
S3 若S≥450,则执行S4,否则执行S10;
S4 若a≥95,则执行S5,否则执行S10;
S5 若b≥95,则执行S6,否则执行S10;
S6 若c≥95,则执行S7,否则执行S10;
S7 若d≥88,则执行S8,否则执行S10;
S8 若e≥88,则执行S9,否则执行S10;
S9 输出“该学生获得学
习优良奖”;
S10 输出“该学生没获
得学习优良奖”.
根据上述算法,其程序框
图如图所示:
【名师点评】 本例是条件分支结构的实际应用,解题的关键是找出所有的判断条件.
变式训练4 某高中男子体育小组的50 m成绩(单位:s)如下:6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5,设计一个算法,从这些成绩中搜索小于6.8 s的成绩,并画出程序框图.
解:算法步骤如下:
S1 i=1;
S2 输入一个数据a;
S3 如果a<6.8,则输出a,
否则不输出,执行S4;
S4 i=i+1;
S5 如果i≤9,则执行S2;
否则结束算法.
程序框图如图所示.
1.程序框图包括顺序结构、条件分支结构和循环结构三种,正确画出算法的程序框图应建立在对算法透彻分析的基础上.
2.仔细审题,在画出程序框图时首先应进行结构的选择,套用公式,若求只含有一个关系式的解析式的函数值时,只用顺序结构就能解决;若是分段函数或被执行时需先判断后才能执行后继步骤的,就必需引入条件分支结构;
方法感悟
如果问题中涉及的运算进行了许多重复的步骤,且数之间有相同的规律,则可引入变量,应用循环结构,当然循环结构中一定用到顺序结构和条件分支结构.
3.具体绘制程序框图时,应注意以下几点:
(1)流程线上要有标志执行顺序的箭头;
(2)判断框后边的流程线应根据情况标注“是”或“否”;
(3)框图内的内容包括累计变量初始值、代数变量初始值、累加值,前后两个变量的差值都要仔细斟酌,不可有丝毫差错;
(4)判断框内内容的填写,有时大于等于,有时大于,有时小于,有时小于等于.它们的含义各不相同,应根据所选循环的类型,正确进行选择.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
