【2012优化方案同步课件】人教B版 数学:必修3 第2章2.3.2
文档属性
| 名称 | 【2012优化方案同步课件】人教B版 数学:必修3 第2章2.3.2 |

|
|
| 格式 | rar | ||
| 文件大小 | 805.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-14 08:12:54 | ||
图片预览










文档简介
(共36张PPT)
2.3.2 两个变量的线性相关
2.3.2
两
个
变
量
的
线
性
相
关
课堂互动讲练
知能优化训练
课前自主学案
学习目标
1.了解线性回归的思想方法(即最小二乘法思想).
2.会求两个具有线性相关关系的变量间的线性回归方程.
课前自主学案
变量与变量之间的关系:①函数关系;②相关关系.
温故夯基
知新益能
1.线性相关关系
____________________表示的相关关系,叫做线性相关关系.如果在散点图中,
___________________________,则称这两个量具有线性相关关系.
2.线性回归方程
一般地,设有(x,y)的n对观察数据如下:
能用直线方程近似
各点都集中在一条直线附近
x x1 x2 x3 … xn
y y1 y2 y3 … yn
当a,b使Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2取得最小值时,就称=bx+a为拟合这n对数据的________________,将该方程所表示的直线称为_____________
3.线性回归方程的系数计算公式
线性回归方程=bx+a中的系数a,b满足:
线性回归方程
回归直线.
思考感悟
回归直线通过样本点中心吗?
4.最小二乘法
通过求Q=______________________的最小值而得出回归直线的方法,即求回归直线,使得样本数据的点到它的距离的平方和最小,这一方法叫做__________________
最小二乘法.
课堂互动讲练
求回归直线方程
考点突破
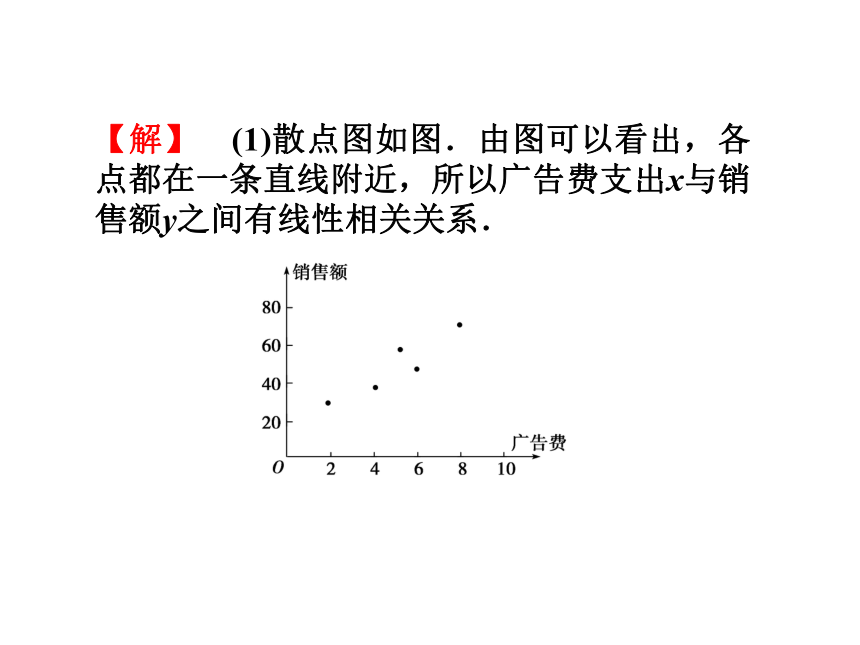
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
例1
x 2 4 5 6 8
y 30 40 60 50 70
(1)画出散点图,判断变量x与y是否具有线性相关关系;
(2)如果x与y具有线性相关关系,求回归直线方程.
【解】 (1)散点图如图.由图可以看出,各点都在一条直线附近,所以广告费支出x与销售额y之间有线性相关关系.
【名师点评】 (1)回归分析是寻找相关关系中非确定性关系的某种确定性.
(2)散点图形象地反映了各对数据的密切程度,并可判断变量间有无相关关系.
(3)求回归直线的方程,关键在于正确地求出系数a、b,由于a、b的计算量较大,计算时要仔细谨慎、分层进行,避免失误.
(4)注意回归直线方程中一次项系数为b,常数项为a,与一次函数的表示习惯不同.
变式训练1 观察两相关变量得如下数据:
求两变量间的回归直线方程.
x -1 -2 -3 -4 -5 5 4 3 2 1
y -9 -7 -5 -3 -1 1 3 5 7 9
解:列表:
i 1 2 3 4 5 6 7 8 9 10
xi -1 -2 -3 -4 -5 5 4 3 2 1
yi -9 -7 -5 -3 -1 1 3 5 7 9
xiyi 9 14 15 12 5 5 12 15 14 9
利用回归直线方程进行估计
例2
下面是我国居民生活污水排放量的一组数据:
年份 2000 2001 2002 2003 2004 2005 2006 2007
排放量 151 189.1 194.8 203.8 220.9 227.7 232.3
试估计2001年我国居民生活污水排放量,并预测2011年生活污水排放量(单位:108 t).
【思路点拨】 要估计或预测,可考虑先求出回归直线方程,将年份与污水排放量的相关关系表达出来.
【解】 设2000年为第1年,…,2007年为第8年.列表,用科学计算器进行有关计算:
i 1 2 3 4 5 6 7
xi 1 3 4 5 6 7 8
yi 151 189.1 194.8 203.8 220.9 227.7 232.3
xiyi 151 567.3 779.2 1019 1325.4 1593.9 1858.4
=4.857,=202.8,=200,iyi=7294.2
【名师点评】 灵活选取数据可以简化运算,当只要求分析两变量相关关系,从而解决实际问题时,可选取恰当的变量进行分析.
第几年 1 2 3 4 5
城市居民年
收入x(亿元) 32.2 31.1 32.9 35.8 37.1
某商品销售
额y(万元) 25.0 30.0 34.0 37.0 39.0
变式训练2 在10年期间,一城市居民的收入与某种商品的销售额之间的关系见下表:
第几年 6 7 8 9 10
城市居民年
收入x(亿元) 38.0 39.0 43.0 44.6 46.0
某商品销售
额y(万元) 41.0 42.0 44.0 48.0 51.0
(1)画出散点图;
(2)如果散点图中各点大致分布在一条直线的附近,求y与x之间的回归直线方程;
(3)试预测居民年收入50亿元时这种商品的销售额.
解:(1)散点图如图所示.
(2)观察散点图可知各点大
致分布在某条直线附近.
列表,利用计算器进行计算.
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据:
回归直线方程的应用
x 3 4 5 6
y 2.5 3 4 4.5
例3
【思路点拨】 由题目可获取以下主要信息:
①甲产品产量x(吨)与相应的生产能耗y(吨)的数据统计表.
②要求画出散点图并利用最小二乘法求回归直线方程.
③根据(2)中求出的回归直线方程进行预测.
解答本题可先画出散点图,再利用最小二乘法求回归直线方程,最后进行预测.
【解】 (1)由题设所给数据,可得散点图如下图所示.
(3)由(2)的回归方程及技改前生产100吨甲产品的生产能耗,得降低的生产能耗为:
90-(0.7×100+0.35)=19.65(吨标准煤).
【名师点评】 此类问题求回归直线方程是关键,求回归方程的关键是求系数a,b,注意用公式时要先求b,再求a.
方法感悟
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
2.3.2 两个变量的线性相关
2.3.2
两
个
变
量
的
线
性
相
关
课堂互动讲练
知能优化训练
课前自主学案
学习目标
1.了解线性回归的思想方法(即最小二乘法思想).
2.会求两个具有线性相关关系的变量间的线性回归方程.
课前自主学案
变量与变量之间的关系:①函数关系;②相关关系.
温故夯基
知新益能
1.线性相关关系
____________________表示的相关关系,叫做线性相关关系.如果在散点图中,
___________________________,则称这两个量具有线性相关关系.
2.线性回归方程
一般地,设有(x,y)的n对观察数据如下:
能用直线方程近似
各点都集中在一条直线附近
x x1 x2 x3 … xn
y y1 y2 y3 … yn
当a,b使Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2取得最小值时,就称=bx+a为拟合这n对数据的________________,将该方程所表示的直线称为_____________
3.线性回归方程的系数计算公式
线性回归方程=bx+a中的系数a,b满足:
线性回归方程
回归直线.
思考感悟
回归直线通过样本点中心吗?
4.最小二乘法
通过求Q=______________________的最小值而得出回归直线的方法,即求回归直线,使得样本数据的点到它的距离的平方和最小,这一方法叫做__________________
最小二乘法.
课堂互动讲练
求回归直线方程
考点突破
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
例1
x 2 4 5 6 8
y 30 40 60 50 70
(1)画出散点图,判断变量x与y是否具有线性相关关系;
(2)如果x与y具有线性相关关系,求回归直线方程.
【解】 (1)散点图如图.由图可以看出,各点都在一条直线附近,所以广告费支出x与销售额y之间有线性相关关系.
【名师点评】 (1)回归分析是寻找相关关系中非确定性关系的某种确定性.
(2)散点图形象地反映了各对数据的密切程度,并可判断变量间有无相关关系.
(3)求回归直线的方程,关键在于正确地求出系数a、b,由于a、b的计算量较大,计算时要仔细谨慎、分层进行,避免失误.
(4)注意回归直线方程中一次项系数为b,常数项为a,与一次函数的表示习惯不同.
变式训练1 观察两相关变量得如下数据:
求两变量间的回归直线方程.
x -1 -2 -3 -4 -5 5 4 3 2 1
y -9 -7 -5 -3 -1 1 3 5 7 9
解:列表:
i 1 2 3 4 5 6 7 8 9 10
xi -1 -2 -3 -4 -5 5 4 3 2 1
yi -9 -7 -5 -3 -1 1 3 5 7 9
xiyi 9 14 15 12 5 5 12 15 14 9
利用回归直线方程进行估计
例2
下面是我国居民生活污水排放量的一组数据:
年份 2000 2001 2002 2003 2004 2005 2006 2007
排放量 151 189.1 194.8 203.8 220.9 227.7 232.3
试估计2001年我国居民生活污水排放量,并预测2011年生活污水排放量(单位:108 t).
【思路点拨】 要估计或预测,可考虑先求出回归直线方程,将年份与污水排放量的相关关系表达出来.
【解】 设2000年为第1年,…,2007年为第8年.列表,用科学计算器进行有关计算:
i 1 2 3 4 5 6 7
xi 1 3 4 5 6 7 8
yi 151 189.1 194.8 203.8 220.9 227.7 232.3
xiyi 151 567.3 779.2 1019 1325.4 1593.9 1858.4
=4.857,=202.8,=200,iyi=7294.2
【名师点评】 灵活选取数据可以简化运算,当只要求分析两变量相关关系,从而解决实际问题时,可选取恰当的变量进行分析.
第几年 1 2 3 4 5
城市居民年
收入x(亿元) 32.2 31.1 32.9 35.8 37.1
某商品销售
额y(万元) 25.0 30.0 34.0 37.0 39.0
变式训练2 在10年期间,一城市居民的收入与某种商品的销售额之间的关系见下表:
第几年 6 7 8 9 10
城市居民年
收入x(亿元) 38.0 39.0 43.0 44.6 46.0
某商品销售
额y(万元) 41.0 42.0 44.0 48.0 51.0
(1)画出散点图;
(2)如果散点图中各点大致分布在一条直线的附近,求y与x之间的回归直线方程;
(3)试预测居民年收入50亿元时这种商品的销售额.
解:(1)散点图如图所示.
(2)观察散点图可知各点大
致分布在某条直线附近.
列表,利用计算器进行计算.
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据:
回归直线方程的应用
x 3 4 5 6
y 2.5 3 4 4.5
例3
【思路点拨】 由题目可获取以下主要信息:
①甲产品产量x(吨)与相应的生产能耗y(吨)的数据统计表.
②要求画出散点图并利用最小二乘法求回归直线方程.
③根据(2)中求出的回归直线方程进行预测.
解答本题可先画出散点图,再利用最小二乘法求回归直线方程,最后进行预测.
【解】 (1)由题设所给数据,可得散点图如下图所示.
(3)由(2)的回归方程及技改前生产100吨甲产品的生产能耗,得降低的生产能耗为:
90-(0.7×100+0.35)=19.65(吨标准煤).
【名师点评】 此类问题求回归直线方程是关键,求回归方程的关键是求系数a,b,注意用公式时要先求b,再求a.
方法感悟
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
