【2012优化方案同步课件】人教B版 数学:必修3 第3章§3.4
文档属性
| 名称 | 【2012优化方案同步课件】人教B版 数学:必修3 第3章§3.4 |

|
|
| 格式 | rar | ||
| 文件大小 | 504.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-14 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
§3.4 概率的应用
3.4
概
率
的
应
用
课堂互动讲练
知能优化训练
课前自主学案
学习目标
1.通过实例,体会概率知识在现实生活中的广泛应用.
2.通过问题的解决,进一步提高对所学知识的掌握与应用.
3.提高运用所学知识分析问题、解决问题的能力与技巧,增加应用意识.
4.通过实例让学生更好的认识生活中诸多现象,提强辨别能力.
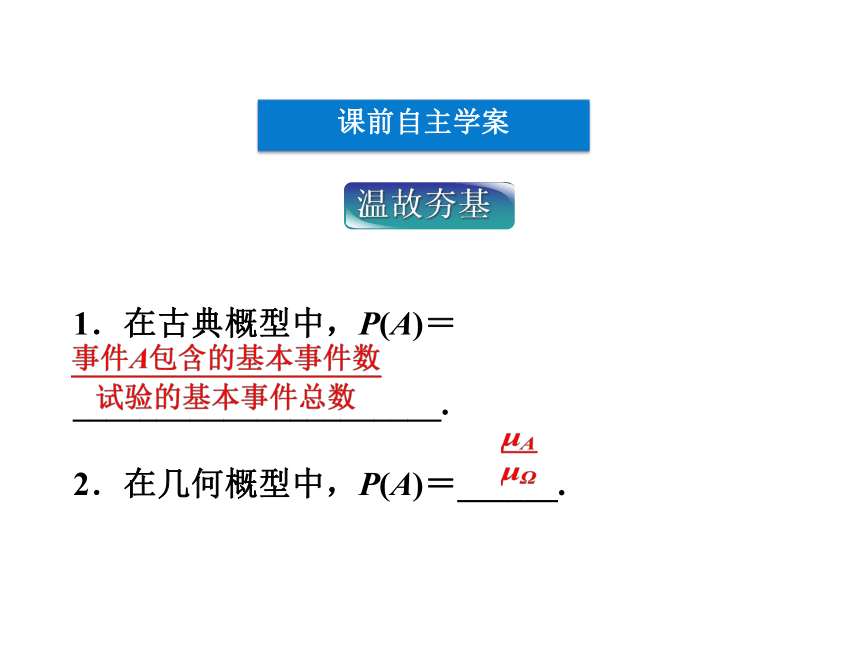
1.在古典概型中,P(A)=
______________________.
2.在几何概型中,P(A)=______.
课前自主学案
温故夯基
概率在我们的现实生活中有很多应用,比如说,利用投硬币出现__________________________来决定足球比赛两球队谁先开球或谁先选场地,用摇号的方法决定中奖号码等等.实际上,概率的应用已涉及到很多领域,如本节课介绍的程序设计、密码技术、社会技术、社会调查(Warner随机化应答方法等)、估计整体等等.
知新益能
正面和反面的概率一样
课堂互动讲练
概率在现实生活中的应用
考点突破
在一场乒乓球的比赛前,要决定由谁先发球,可用下面的方法:裁判员拿出一抽签器,它是一个像大硬币似的均匀塑料圆板,一面是红色,一面是绿色,然后随意指定一名运动员,让他猜上抛的抽签器落到球台上时,是红色那面朝上还是绿色那面朝上,如果他猜对了,就由他先发球,否则,由另一方发球,试作出解释.
例1
【思路点拨】 就其概率大小作出解释.
【解】 这样做体现了公平性,它使得两名运动员的谁先发球的机会是等可能的.用概率的语言描述,就是两个运动员取得发球权的概率都是0.5,即任何一名运动员猜中的概率都是0.5,也就是每个运动员先发球的概率均为0.5,所以这个规则是公平的.
【名师点评】 足球比赛中用抛掷硬币的方式来确定场地也是这个原因.
变式训练1 在生活中我们有时要用抽签的方法来决定一件事情,例如5张票中有1张奖票,5个人按照顺序从中各抽1张以决定谁得到其中的奖票,那么,先抽还是后抽(后抽人不知道先抽人抽出的结果)对各人来说公平吗?也就是说,各人抽到奖票的概率相等吗?
假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,2,…,9十个数字中的任意一个.假设一个人完全忘记了自己的储蓄卡密码,问他到自动取款机上试一次密码就能取到钱的概率是多少?
随机事件的概率
例2
【思路点拨】 发生概率为0.0001的事件是小概率事件,通常我们认为这样的事件一次试验中是几乎不可能发生的,也就是通过随机试验的方法取到储蓄卡中的钱的概率是很小的.但我们知道,如果试验很多次,比如10000次,那么这个小概率事件是可能发生的.所以,为了安全,自动取款机一般允许取款人最多试3次密码,如果第4次键入的号码仍是错误的,那么取款机将“没收”储蓄卡.另外,为了使通过随机试验的方法取到的储蓄卡中的钱的概率更小,现在储蓄卡大多使用6位数字作密码.
变式训练2 某城市的电话号码是8位数,如果从电话号码本中任取一个电话号码,求:
(1)头两位数码都是8的概率;
(2)头两位数码都不超过8的概率.
解:电话号码每位上的数字都可以由0,1,2,…,9十个数字中的任一个数字组成,故试验基本事件总数为n=108.
(1)记“头两位数码都是8”为事件A,则事件A的一、二两位数码都只有一种选法,即只能选8,后六位各有10种选法,故事件A包含的基本事件数为m1=1×1×106=106.
几何概型的应用
甲、乙两艘船都要停靠同一个泊位,它们可能在一昼夜的任意时刻到达,如果甲、乙两艘船停靠泊位的时间分别是2小时与4小时,求有一艘船停靠泊位时必须等待一段时间的概率.
例3
【思路点拨】 如图,当甲比乙早到2小时内乙需等待,甲比乙晚到4小时内甲需等待,所以有一艘船停靠泊位时必须等待一段时间等价于-2≤x-y≤4.
【解】 用x和y分别表示甲、乙两船到达泊位的时间,则有一艘船停靠泊位时必须等待一段时间的充要条件是-2≤x-y≤4,在平面直角坐标系内,(x,y)的所有可能结果是边长为24的正方形,而事件A“有一艘船停靠泊位时必须等待一段时间”的所有可能结果为阴影部分表示.
【名师点评】 要善于利用数形结合,将实际问题转化为数学问题,根据几何概型的定义、特点,会用公式计算几何概型.
1.处理概率的应用题要精读问题,抓住关键词语,将问题转化为数学问题.
2.涉及随机事件概率时主要向古典概型与几何概型方面的问题靠拢.
3.处理较复杂的问题时,要注意相关事件的互斥性,合理运用概率的加法公式.
4.解决应用题应注意多方面知识的综合运用.
方法感悟
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
§3.4 概率的应用
3.4
概
率
的
应
用
课堂互动讲练
知能优化训练
课前自主学案
学习目标
1.通过实例,体会概率知识在现实生活中的广泛应用.
2.通过问题的解决,进一步提高对所学知识的掌握与应用.
3.提高运用所学知识分析问题、解决问题的能力与技巧,增加应用意识.
4.通过实例让学生更好的认识生活中诸多现象,提强辨别能力.
1.在古典概型中,P(A)=
______________________.
2.在几何概型中,P(A)=______.
课前自主学案
温故夯基
概率在我们的现实生活中有很多应用,比如说,利用投硬币出现__________________________来决定足球比赛两球队谁先开球或谁先选场地,用摇号的方法决定中奖号码等等.实际上,概率的应用已涉及到很多领域,如本节课介绍的程序设计、密码技术、社会技术、社会调查(Warner随机化应答方法等)、估计整体等等.
知新益能
正面和反面的概率一样
课堂互动讲练
概率在现实生活中的应用
考点突破
在一场乒乓球的比赛前,要决定由谁先发球,可用下面的方法:裁判员拿出一抽签器,它是一个像大硬币似的均匀塑料圆板,一面是红色,一面是绿色,然后随意指定一名运动员,让他猜上抛的抽签器落到球台上时,是红色那面朝上还是绿色那面朝上,如果他猜对了,就由他先发球,否则,由另一方发球,试作出解释.
例1
【思路点拨】 就其概率大小作出解释.
【解】 这样做体现了公平性,它使得两名运动员的谁先发球的机会是等可能的.用概率的语言描述,就是两个运动员取得发球权的概率都是0.5,即任何一名运动员猜中的概率都是0.5,也就是每个运动员先发球的概率均为0.5,所以这个规则是公平的.
【名师点评】 足球比赛中用抛掷硬币的方式来确定场地也是这个原因.
变式训练1 在生活中我们有时要用抽签的方法来决定一件事情,例如5张票中有1张奖票,5个人按照顺序从中各抽1张以决定谁得到其中的奖票,那么,先抽还是后抽(后抽人不知道先抽人抽出的结果)对各人来说公平吗?也就是说,各人抽到奖票的概率相等吗?
假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,2,…,9十个数字中的任意一个.假设一个人完全忘记了自己的储蓄卡密码,问他到自动取款机上试一次密码就能取到钱的概率是多少?
随机事件的概率
例2
【思路点拨】 发生概率为0.0001的事件是小概率事件,通常我们认为这样的事件一次试验中是几乎不可能发生的,也就是通过随机试验的方法取到储蓄卡中的钱的概率是很小的.但我们知道,如果试验很多次,比如10000次,那么这个小概率事件是可能发生的.所以,为了安全,自动取款机一般允许取款人最多试3次密码,如果第4次键入的号码仍是错误的,那么取款机将“没收”储蓄卡.另外,为了使通过随机试验的方法取到的储蓄卡中的钱的概率更小,现在储蓄卡大多使用6位数字作密码.
变式训练2 某城市的电话号码是8位数,如果从电话号码本中任取一个电话号码,求:
(1)头两位数码都是8的概率;
(2)头两位数码都不超过8的概率.
解:电话号码每位上的数字都可以由0,1,2,…,9十个数字中的任一个数字组成,故试验基本事件总数为n=108.
(1)记“头两位数码都是8”为事件A,则事件A的一、二两位数码都只有一种选法,即只能选8,后六位各有10种选法,故事件A包含的基本事件数为m1=1×1×106=106.
几何概型的应用
甲、乙两艘船都要停靠同一个泊位,它们可能在一昼夜的任意时刻到达,如果甲、乙两艘船停靠泊位的时间分别是2小时与4小时,求有一艘船停靠泊位时必须等待一段时间的概率.
例3
【思路点拨】 如图,当甲比乙早到2小时内乙需等待,甲比乙晚到4小时内甲需等待,所以有一艘船停靠泊位时必须等待一段时间等价于-2≤x-y≤4.
【解】 用x和y分别表示甲、乙两船到达泊位的时间,则有一艘船停靠泊位时必须等待一段时间的充要条件是-2≤x-y≤4,在平面直角坐标系内,(x,y)的所有可能结果是边长为24的正方形,而事件A“有一艘船停靠泊位时必须等待一段时间”的所有可能结果为阴影部分表示.
【名师点评】 要善于利用数形结合,将实际问题转化为数学问题,根据几何概型的定义、特点,会用公式计算几何概型.
1.处理概率的应用题要精读问题,抓住关键词语,将问题转化为数学问题.
2.涉及随机事件概率时主要向古典概型与几何概型方面的问题靠拢.
3.处理较复杂的问题时,要注意相关事件的互斥性,合理运用概率的加法公式.
4.解决应用题应注意多方面知识的综合运用.
方法感悟
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
