北师大版2020年七年级上册第4章《基本平面图形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 北师大版2020年七年级上册第4章《基本平面图形》单元测试卷(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 189.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-01 00:00:00 | ||
图片预览





文档简介
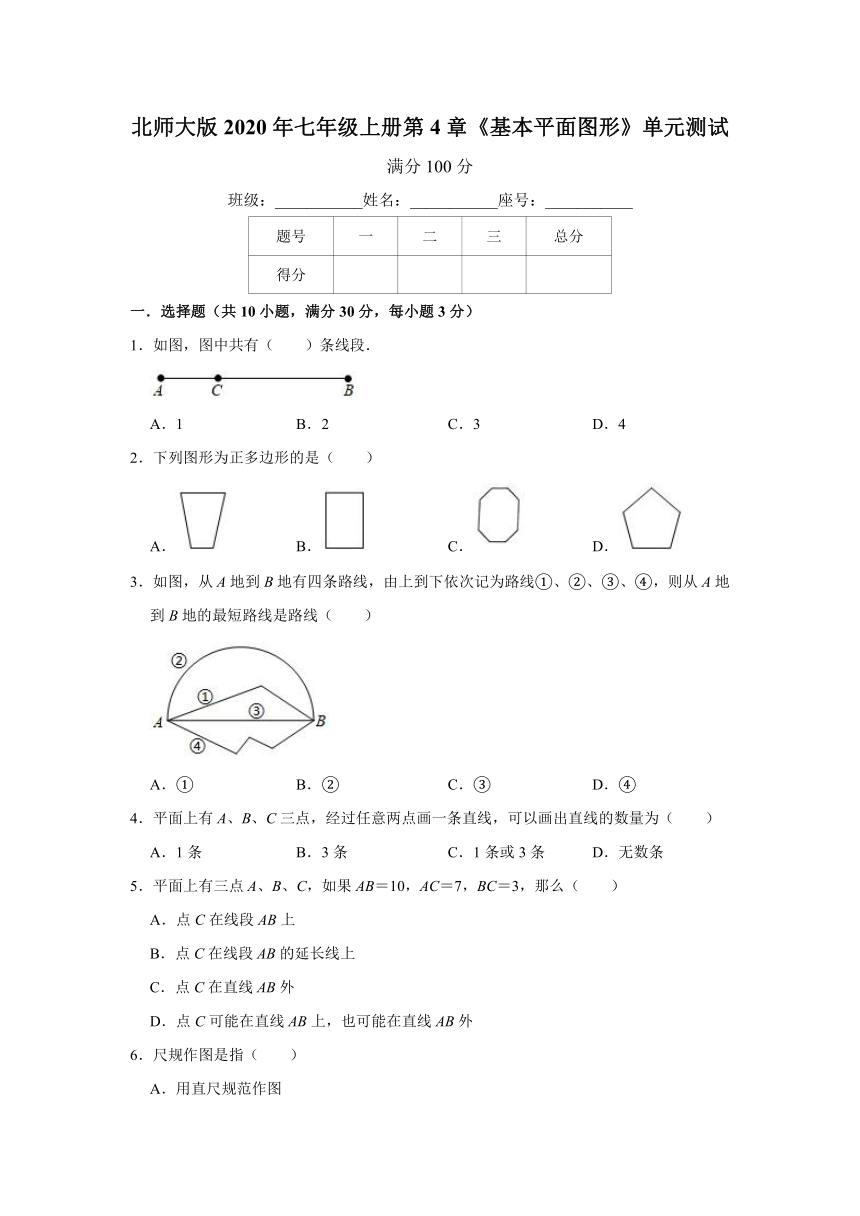
北师大版2020年七年级上册第4章《基本平面图形》单元测试
满分100分
班级:___________姓名:___________座号:___________
题号
一
二
三
总分
得分
一.选择题(共10小题,满分30分,每小题3分)
1.如图,图中共有( )条线段.
A.1
B.2
C.3
D.4
2.下列图形为正多边形的是( )
A.
B.
C.
D.
3.如图,从A地到B地有四条路线,由上到下依次记为路线①、②、③、④,则从A地到B地的最短路线是路线( )
A.①
B.②
C.③
D.④
4.平面上有A、B、C三点,经过任意两点画一条直线,可以画出直线的数量为( )
A.1条
B.3条
C.1条或3条
D.无数条
5.平面上有三点A、B、C,如果AB=10,AC=7,BC=3,那么( )
A.点C在线段AB上
B.点C在线段AB的延长线上
C.点C在直线AB外
D.点C可能在直线AB上,也可能在直线AB外
6.尺规作图是指( )
A.用直尺规范作图
B.用刻度尺和圆规作图
C.用没有刻度的直尺和圆规作图
D.直尺和圆规是作图工具
7.11点40分,时钟的时针与分针的夹角为( )
A.140°
B.130°
C.120°
D.110°
8.若∠A=38°15′,∠B=38.15°,则( )
A.∠A>∠B
B.∠A<∠BC
C.∠A=∠B
D.无法确定
9.如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.48°
B.56°
C.60°
D.32°
10.中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为4cm,圆心角为60°,则图中摆盘的面积是( )
A.80πcm2
B.40πcm2
C.24πcm2
D.2πcm2
二.填空题(共7小题,满分28分,每小题4分)
11.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都
,这个距离就是这个圆的
.
12.如图,建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条直的参照线,这样做的依据是
.
13.35.48°=
度
分
秒.
14.过一个多边形的一个顶点的对角线有6条,则该多边形是
边形.
15.一艘船从A港驶向B港的航向是北偏东25°,则该船返回时的航向应该是
.
16.已知如图,C是线段AB上的一点,N是线段BC的中点,若AB=10,AC=6,则AN=
.
17.已知∠AOB=40°,∠BOC=3∠AOC,则∠AOC的度数是
.
三.解答题(共6小题,满分42分)
18.(6分)如图,已知点A、B、C.D,根据下列语句画图.(不写作图过程)
作射线AB、直线AC,连接AD并延长线段AD.
19.(6分)如图所示,已知BC是从直线AB上出发的一条射线,BE平分∠ABC,∠EBF=90°.求证:BF平分∠CBD.
20.(6分)如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:
(1)图中到小明家距离相同的是哪些地方?
(2)由图可知,公园在小明家东偏南30°方向2km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.
21.(7分)如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
22.(8分)如图(1),线段上有3个点时,线段共有3
条;如图(2)线段上有4个点时,线段共有6条;如图(3)线段上有5个点时,线段共有10条.
(1)当线段上有6个点时,线段共有
条;
(2)当线段上有n个点时,线段共有
条;(用n的代数式表示)
(3)当n=100时,线段共有
条.
23.(9分)已知:∠AOB和∠COD是直角.
(1)如图1,当射线OB在∠COD内部时,请探究∠AOD和∠BOC之间的关系;
(2)如图2,当射线OA,射线OB都在∠COD外部时,过点O作射线OE,射线OF,满足∠BOE=∠BOC,∠DOF=∠AOD,求∠EOF的度数;
(3)如图3,在(2)的条件下,在平面内是否存在射线OG,使得∠GOF:∠GOE=2:3,若不存在,请说明理由,若存在,求出∠GOF的度数.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:图中共有3条线段:线段AC、CB、AB.
故选:C.
2.解:正五边形五个角相等,五条边都相等,
故选:D.
3.解:根据两点之间线段最短可得,从A地到B地的最短路线是路线③.
故选:C.
4.解:①如果三点共线,过其中两点画直线,共可以画1条;
②如果任意三点不共线,过其中两点画直线,共可以画3条.
故选:C.
5.解:如图,在平面内,AB=10,
∵AC=7,BC=3,
∴点C为以A为圆心,7为半径,与以B为圆心,3为半径的两个圆的交点,
由于AB=10=7+3=AC+BC,
所以,点C在线段AB上,
故选:A.
6.解:根据尺规作图的定义可知:尺规作图是指用没有刻度的直尺和圆规作图.
故选:C.
7.解:11点40分时针与分针相距3+=(份),
30°×=110°,
故选:D.
8.解:∵∠A=38°15′,∠B=38.15°=38°9′,
∴∠A>∠B.
故选:A.
9.解:∵OC平分∠AOB,
∴∠AOB=2∠AOC=2∠BOC,
∵∠COD是直角,
∴∠COD=90°,
∵∠BOD=118°,
∴∠BOC=∠BOD﹣∠COD=118°﹣90°=28°,
∴∠AOB=2∠BOC=56°.
故选:B.
10.解:如图,连接CD.
∵OC=OD,∠O=60°,
∴△COD是等边三角形,
∴OC=OD=CD=4cm,
∴S阴=S扇形OAB﹣S扇形OCD=﹣=40π(cm2),
故选:B.
二.填空题(共7小题,满分28分,每小题4分)
11.解:参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都相等,这个距离就是这个圆的半径.
故答案为:相等,半径.
12.解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
13.解:0.48°=(0.48×60)′=28.8′,
0.8′=(0.8×60)″=48″,
所以35.48°=35°28′48″.
故答案为:35,28,48.
14.解:∵过一个多边形的一个顶点的对角线有6条,
∴多边形的边数为6+3=9,
∴这个多边形是九边形.
故答案为九.
15.解:如图,从A港驶向B港的航向是北偏东25°,返回时的航向南偏西25°,
故答案为:南偏西25°.
16.解:∵AB=10,AC=6,
∴CB=10﹣6=4,
∵N是线段BC的中点,
∴CN=2,
∴AN=AC+CN=6+2=8.
17.解:当OC在∠AOB内部时,如图1,
∵∠AOB=40°,∠BOC=3∠AOC,
∴∠AOC=;
当OC在∠AOB外部时,如图2,
∵∠BOC﹣∠AOC=∠AOB,∠AOB=40°,∠BOC=3∠AOC,
∴3∠AOC﹣∠AOC=40°,
∴∠AOC=20°.
综上,∠AOC=10°或20°.
故答案为:10°或20°.
三.解答题(共6小题,满分42分)
18.解:作射线AB、直线AC,连接AD并延长线段AD,如图所示:
19.证明:∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠EBF=90°,
∴∠CBF=90°﹣∠CBE,
∴∠DBF=180°﹣90°﹣∠ABE=90°∠CBE=∠CBF.
即BF平分∠CBD.
20.解:(1)因为点C为OP的中点,
所以OC=2km,
因为OA=2km,
所以可得出距小明家距离相同的是学校和公园;
(2)由图可知,学校在小明家东偏北45°方向2km处,商场在小明家西偏北60°方向3.5km处,停车场在东偏南30°方向4km处.
21.解:(1)①∵AB=CD,
∴AB+BC=CD+BC,
即,AC=BD,
故答案为:=;
②∵BC=AC,且AC=12cm,
∴BC=×12=9(cm),
∴AB=CD=AC﹣BC=12﹣9=3(cm),
∴AD=AC+CD=12+3=15(cm),
故答案为:15;
(2)如图,
设每份为x,则AB=3x,BC=4x,CD=5x,AD=12x,
∵M是AB的中点,点N是CD的中点N,
∴AM=BM=x,CN=DN=x,
又∵MN=16,
∴x+4x+x=16,
解得,x=2,
∴AD=12x=24(cm),
答:AD的长为24cm.
22.解:(1)当线段上有6个点时,线段共有=15条;
(2)当线段上有n个点时,线段共有
条;
(3)当n=100时,线段共有=4950条;
故答案为:15,,4950.
23.(1)∠AOD+∠BOC=180°.
证明:∵∠AOB和∠COD是直角,
∴∠AOB=∠COD=90°,
∵∠BOD+∠BOC=∠COD,
∴∠BOD=90°﹣∠BOC,
同理:∠AOC=90°﹣∠BOC,
∴∠AOD=∠AOB+∠BOD=90°+90°﹣∠BOC=180°﹣∠BOC,
∴∠AOD+∠BOC=180°;
(2)解:设∠BOE=a,则∠BOC=3a,
∵∠BOE+∠EOC=∠BOC,
∴∠EOC=∠BOC﹣∠BOE=2a,
∵∠AOD+∠COD+∠BOC+∠AOB=360°,
∴∠AOD=360°﹣∠COD﹣2
BOC﹣∠AOB
=360°﹣90°﹣3a﹣﹣90°=180°﹣3a,
∵∠DOF=∠AOD,
∴∠DOF=(180°﹣3a)=120°﹣2a,
∴∠AOF=∠AOD=(180°﹣3a)=60°﹣a,
∴∠EOF=∠BOE+∠AOB+∠AOF=a+90°+60°﹣a=150°,
∠EOF的度数为150°;
(3)①当射线OG在∠EOF内部时,
∴∠GOF:∠GOE=2:3,
∴∠GOF=
(∠GOF+∠GOE)=∠EOF=150°=60°;
②当射线OG在∠EOF外部时,
∵∠GOF:∠GOE=2:3,
∴∠GOF=
(∠GOF+∠GOE)
=∠EOF
=(∠DOF+∠COD+∠EOC)
=
(120°﹣2a+90°+2a)
=84°.
综上所述,∠GOF
的度数是60°或84°.
满分100分
班级:___________姓名:___________座号:___________
题号
一
二
三
总分
得分
一.选择题(共10小题,满分30分,每小题3分)
1.如图,图中共有( )条线段.
A.1
B.2
C.3
D.4
2.下列图形为正多边形的是( )
A.
B.
C.
D.
3.如图,从A地到B地有四条路线,由上到下依次记为路线①、②、③、④,则从A地到B地的最短路线是路线( )
A.①
B.②
C.③
D.④
4.平面上有A、B、C三点,经过任意两点画一条直线,可以画出直线的数量为( )
A.1条
B.3条
C.1条或3条
D.无数条
5.平面上有三点A、B、C,如果AB=10,AC=7,BC=3,那么( )
A.点C在线段AB上
B.点C在线段AB的延长线上
C.点C在直线AB外
D.点C可能在直线AB上,也可能在直线AB外
6.尺规作图是指( )
A.用直尺规范作图
B.用刻度尺和圆规作图
C.用没有刻度的直尺和圆规作图
D.直尺和圆规是作图工具
7.11点40分,时钟的时针与分针的夹角为( )
A.140°
B.130°
C.120°
D.110°
8.若∠A=38°15′,∠B=38.15°,则( )
A.∠A>∠B
B.∠A<∠BC
C.∠A=∠B
D.无法确定
9.如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.48°
B.56°
C.60°
D.32°
10.中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为4cm,圆心角为60°,则图中摆盘的面积是( )
A.80πcm2
B.40πcm2
C.24πcm2
D.2πcm2
二.填空题(共7小题,满分28分,每小题4分)
11.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都
,这个距离就是这个圆的
.
12.如图,建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条直的参照线,这样做的依据是
.
13.35.48°=
度
分
秒.
14.过一个多边形的一个顶点的对角线有6条,则该多边形是
边形.
15.一艘船从A港驶向B港的航向是北偏东25°,则该船返回时的航向应该是
.
16.已知如图,C是线段AB上的一点,N是线段BC的中点,若AB=10,AC=6,则AN=
.
17.已知∠AOB=40°,∠BOC=3∠AOC,则∠AOC的度数是
.
三.解答题(共6小题,满分42分)
18.(6分)如图,已知点A、B、C.D,根据下列语句画图.(不写作图过程)
作射线AB、直线AC,连接AD并延长线段AD.
19.(6分)如图所示,已知BC是从直线AB上出发的一条射线,BE平分∠ABC,∠EBF=90°.求证:BF平分∠CBD.
20.(6分)如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:
(1)图中到小明家距离相同的是哪些地方?
(2)由图可知,公园在小明家东偏南30°方向2km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.
21.(7分)如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
22.(8分)如图(1),线段上有3个点时,线段共有3
条;如图(2)线段上有4个点时,线段共有6条;如图(3)线段上有5个点时,线段共有10条.
(1)当线段上有6个点时,线段共有
条;
(2)当线段上有n个点时,线段共有
条;(用n的代数式表示)
(3)当n=100时,线段共有
条.
23.(9分)已知:∠AOB和∠COD是直角.
(1)如图1,当射线OB在∠COD内部时,请探究∠AOD和∠BOC之间的关系;
(2)如图2,当射线OA,射线OB都在∠COD外部时,过点O作射线OE,射线OF,满足∠BOE=∠BOC,∠DOF=∠AOD,求∠EOF的度数;
(3)如图3,在(2)的条件下,在平面内是否存在射线OG,使得∠GOF:∠GOE=2:3,若不存在,请说明理由,若存在,求出∠GOF的度数.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:图中共有3条线段:线段AC、CB、AB.
故选:C.
2.解:正五边形五个角相等,五条边都相等,
故选:D.
3.解:根据两点之间线段最短可得,从A地到B地的最短路线是路线③.
故选:C.
4.解:①如果三点共线,过其中两点画直线,共可以画1条;
②如果任意三点不共线,过其中两点画直线,共可以画3条.
故选:C.
5.解:如图,在平面内,AB=10,
∵AC=7,BC=3,
∴点C为以A为圆心,7为半径,与以B为圆心,3为半径的两个圆的交点,
由于AB=10=7+3=AC+BC,
所以,点C在线段AB上,
故选:A.
6.解:根据尺规作图的定义可知:尺规作图是指用没有刻度的直尺和圆规作图.
故选:C.
7.解:11点40分时针与分针相距3+=(份),
30°×=110°,
故选:D.
8.解:∵∠A=38°15′,∠B=38.15°=38°9′,
∴∠A>∠B.
故选:A.
9.解:∵OC平分∠AOB,
∴∠AOB=2∠AOC=2∠BOC,
∵∠COD是直角,
∴∠COD=90°,
∵∠BOD=118°,
∴∠BOC=∠BOD﹣∠COD=118°﹣90°=28°,
∴∠AOB=2∠BOC=56°.
故选:B.
10.解:如图,连接CD.
∵OC=OD,∠O=60°,
∴△COD是等边三角形,
∴OC=OD=CD=4cm,
∴S阴=S扇形OAB﹣S扇形OCD=﹣=40π(cm2),
故选:B.
二.填空题(共7小题,满分28分,每小题4分)
11.解:参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都相等,这个距离就是这个圆的半径.
故答案为:相等,半径.
12.解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
13.解:0.48°=(0.48×60)′=28.8′,
0.8′=(0.8×60)″=48″,
所以35.48°=35°28′48″.
故答案为:35,28,48.
14.解:∵过一个多边形的一个顶点的对角线有6条,
∴多边形的边数为6+3=9,
∴这个多边形是九边形.
故答案为九.
15.解:如图,从A港驶向B港的航向是北偏东25°,返回时的航向南偏西25°,
故答案为:南偏西25°.
16.解:∵AB=10,AC=6,
∴CB=10﹣6=4,
∵N是线段BC的中点,
∴CN=2,
∴AN=AC+CN=6+2=8.
17.解:当OC在∠AOB内部时,如图1,
∵∠AOB=40°,∠BOC=3∠AOC,
∴∠AOC=;
当OC在∠AOB外部时,如图2,
∵∠BOC﹣∠AOC=∠AOB,∠AOB=40°,∠BOC=3∠AOC,
∴3∠AOC﹣∠AOC=40°,
∴∠AOC=20°.
综上,∠AOC=10°或20°.
故答案为:10°或20°.
三.解答题(共6小题,满分42分)
18.解:作射线AB、直线AC,连接AD并延长线段AD,如图所示:
19.证明:∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠EBF=90°,
∴∠CBF=90°﹣∠CBE,
∴∠DBF=180°﹣90°﹣∠ABE=90°∠CBE=∠CBF.
即BF平分∠CBD.
20.解:(1)因为点C为OP的中点,
所以OC=2km,
因为OA=2km,
所以可得出距小明家距离相同的是学校和公园;
(2)由图可知,学校在小明家东偏北45°方向2km处,商场在小明家西偏北60°方向3.5km处,停车场在东偏南30°方向4km处.
21.解:(1)①∵AB=CD,
∴AB+BC=CD+BC,
即,AC=BD,
故答案为:=;
②∵BC=AC,且AC=12cm,
∴BC=×12=9(cm),
∴AB=CD=AC﹣BC=12﹣9=3(cm),
∴AD=AC+CD=12+3=15(cm),
故答案为:15;
(2)如图,
设每份为x,则AB=3x,BC=4x,CD=5x,AD=12x,
∵M是AB的中点,点N是CD的中点N,
∴AM=BM=x,CN=DN=x,
又∵MN=16,
∴x+4x+x=16,
解得,x=2,
∴AD=12x=24(cm),
答:AD的长为24cm.
22.解:(1)当线段上有6个点时,线段共有=15条;
(2)当线段上有n个点时,线段共有
条;
(3)当n=100时,线段共有=4950条;
故答案为:15,,4950.
23.(1)∠AOD+∠BOC=180°.
证明:∵∠AOB和∠COD是直角,
∴∠AOB=∠COD=90°,
∵∠BOD+∠BOC=∠COD,
∴∠BOD=90°﹣∠BOC,
同理:∠AOC=90°﹣∠BOC,
∴∠AOD=∠AOB+∠BOD=90°+90°﹣∠BOC=180°﹣∠BOC,
∴∠AOD+∠BOC=180°;
(2)解:设∠BOE=a,则∠BOC=3a,
∵∠BOE+∠EOC=∠BOC,
∴∠EOC=∠BOC﹣∠BOE=2a,
∵∠AOD+∠COD+∠BOC+∠AOB=360°,
∴∠AOD=360°﹣∠COD﹣2
BOC﹣∠AOB
=360°﹣90°﹣3a﹣﹣90°=180°﹣3a,
∵∠DOF=∠AOD,
∴∠DOF=(180°﹣3a)=120°﹣2a,
∴∠AOF=∠AOD=(180°﹣3a)=60°﹣a,
∴∠EOF=∠BOE+∠AOB+∠AOF=a+90°+60°﹣a=150°,
∠EOF的度数为150°;
(3)①当射线OG在∠EOF内部时,
∴∠GOF:∠GOE=2:3,
∴∠GOF=
(∠GOF+∠GOE)=∠EOF=150°=60°;
②当射线OG在∠EOF外部时,
∵∠GOF:∠GOE=2:3,
∴∠GOF=
(∠GOF+∠GOE)
=∠EOF
=(∠DOF+∠COD+∠EOC)
=
(120°﹣2a+90°+2a)
=84°.
综上所述,∠GOF
的度数是60°或84°.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
