2020-2021学年九年级数学北师大版第三章第一节《用树状图或表格求概率》同步练习(word有答案)
文档属性
| 名称 | 2020-2021学年九年级数学北师大版第三章第一节《用树状图或表格求概率》同步练习(word有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-01 21:49:12 | ||
图片预览



文档简介
第1节
用树状图或表格求概率(1)
1、甲、乙、丙三人站成一排拍照,则甲站在中间的概率是(
)
A.
B.
C.
D.
2、有三张正面分别写有数字-2,1,3
的卡片,它们的背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为
a
的值,然后把这张卡片放回去,洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为
b
的值,则点(a,b)在第一象限内的概率为(
)
A.
B.
C.
D.
3、小明和小亮在玩“石头、剪刀、布”的游戏,则两人一起做同样手势的概率是(
)
A.
B.
C.
D.
4、小蕾有某文学名著上、中、下各
1
册,她随机将它们叠放在一起,从上到下的顺序恰好为“上册、中册、下册”的概率是
.
5、从
1、2、3
中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的
数字,那么组成的两位数是
4
的倍数的概率是
.
6、从-2,-1,2
这三个数中任取两个不同的数相乘,则积为正数的概率是
.
7、三张反面完全相同的卡片,正面分别写有“木”“寸”“木”,把它们洗匀后,反面朝上,任取两张,能拼成“村”字的概率是
.
8、在一个箱内装入只有标号不同的三颗小球,标号分别为
1,2,3.每次随机取出一颗小球,记下标号作为得分,再将小球放回箱内.小明现已取球三次,得分分别为1
分,3
分,2
分,小明又从箱内取球两次,若五次得分的平均数不小于
2.2
分,请用画树状图或列表的方法,求发生“五次取球得分的平均数不小于
2.2
分”情况的概率.
9、有甲、乙两个不透明的布袋,甲袋中只装有
3
个除标号外完全相同的小球,分别标有数字0,1,2;乙袋中只装有
3
个除标号外完全相同的小球,分别标有数字-1,-2,0.现从甲袋中随机抽取一个小球,记录标有的数字为
x,再从乙袋中随机抽取一个小球,记录标有的数字为
y,由此确定点
M
的坐标为(x,y).
(1)写出点
M
所有可能的坐标;
(2)求点
M(x,y)在函数
y=-x+1
的图象上的概率.
答案
1.B
2.D
3.B
4.
5.
6.
7.
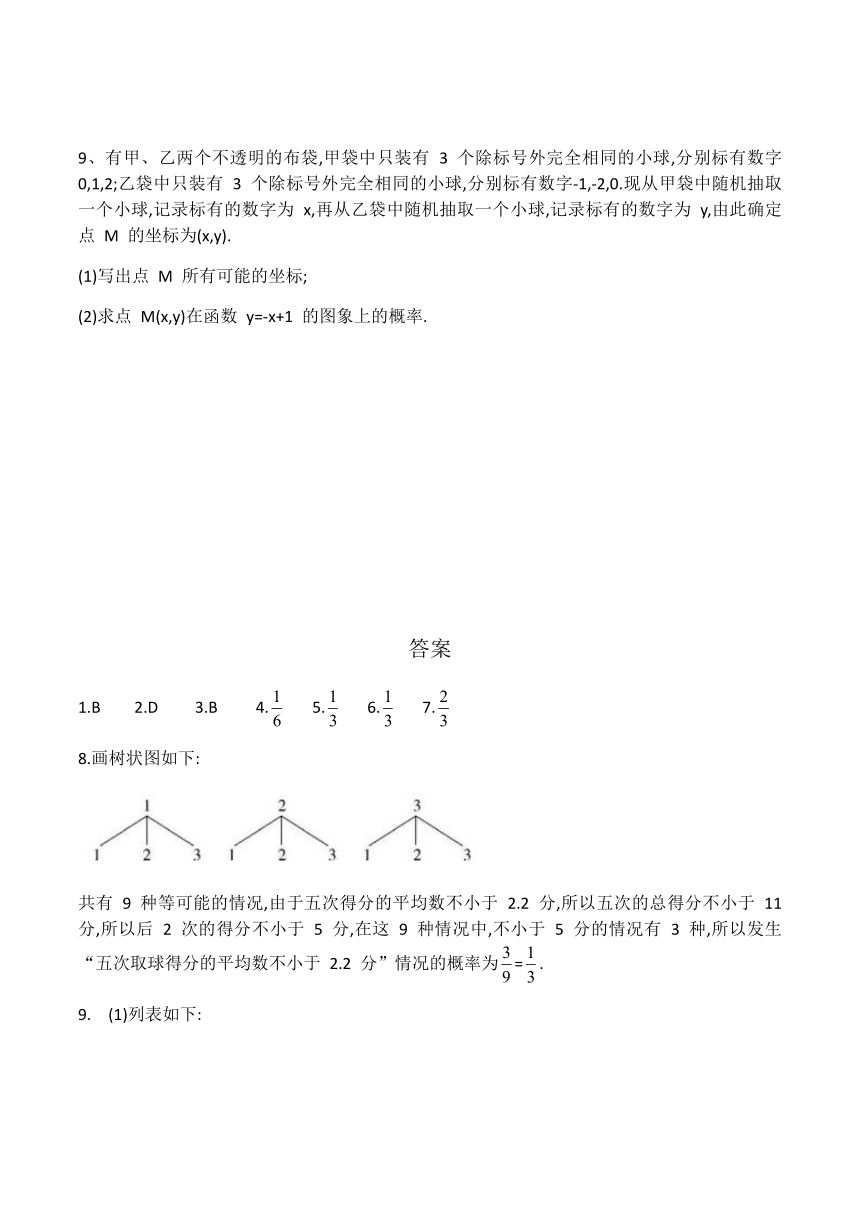
8.画树状图如下:
共有
9
种等可能的情况,由于五次得分的平均数不小于
2.2
分,所以五次的总得分不小于
11
分,所以后
2
次的得分不小于
5
分,在这
9
种情况中,不小于
5
分的情况有
3
种,所以发生“五次取球得分的平均数不小于
2.2
分”情况的概率为=.
9.
(1)列表如下:
(2)由(1)知,共有
9
种等可能的结果,满足点
M(x,y)在函数
y=-x+1
的图象上的结果有
2
个,即(2,-1),(1,0),所以点
M(x,y)在函数
y=-x+1
的图象上的概率为.
第1节
用树状图或表格求概率(2)
1、如图,两个转盘(每个转盘被分成面积相等的
4
个扇形)分别自由转动一次,当停止转动时,两个转盘的指针都指向
2
的概率为(
)
A.
B.
C.
D.
2、经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种情况的可能性大小相同,则事件“两辆车向右转,一辆车向左转”的概率为(
)
A.
B.
C.
D.
3、假定鸟卵孵化后,雏鸟为雌与雄的概率相同.若三枚卵全部成功孵化,则三只雏鸟中恰有两只雄鸟的概率是(
)
A.
B.
C.
D.
4、5
月
19
日为中国旅游日,某市推出旅游惠民活动,市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个景点游玩;下午从江郎山、三衢石林、开化根博园中随机选择一个景点游玩,则王先生恰好上午选中孔氏南宗家庙,下午选中江郎山的概率是(
)
A.
B.
C.
D.
5、某校甲、乙、丙、丁四名同学在运动会上参加
4×100
米接力比赛,其中甲跑第一棒,乙跑第二棒的概率是(
)
A.
B.
C.
D.
6、一个不透明的布袋中仅有
2
个红球,1
个黑球,这些球除颜色外无其他差别,先随机摸出一个小球,记下颜色后放回搅匀,再随机摸出一个小球,则两次摸出的小球颜色不同的概率是
.
7、如图,
随机闭合开关
S1,S2,S3
中的两个,能让灯泡发光的概率
是.
8、一个不透明的口袋中有三个小球,每个小球上只标有一个汉字,分别是“家”“家”“乐”,除汉字外其余均相同.小新同学从口袋中随机摸出一个小球,记下汉字后放回并搅匀;再从口袋中随机摸出一个小球记下汉字.用画树状图(或列表)的方法,求小新同学两次摸出小球上的汉字相同的概率.
9、在一个不透明的口袋中装有
4
张纸牌,纸牌上分别标有数字
1,2,3,4,除数字外其余均相同.洗匀后,随机摸出一张纸牌,然后放回,洗匀,再随机摸出一张纸牌.
(1)计算两次摸出的纸牌上数字之和为
5
的概率;
(2)甲、乙两个人进行游戏,若两次摸出的纸牌上数字之和为奇数,则甲胜;若两次摸出的纸牌上数字之和为偶数,则乙胜.这个游戏公平吗?请说明理由.
10、甲口袋中装有
2
张相同的卡片,它们分别写有数字
2
和
3;乙口袋中装有
3
张相同的卡片,它们分别写有数字
4,5
和
6;丙口袋中装有
2
张相同的卡片,它们分别写有数字
7
和
8.从三个口袋中各随机取出
1
张卡片.
(1)取出的
3
张卡片中,恰好
3
个数都是偶数的概率是多少?
(2)取出的
3
张卡片上的数字之和共有几种不同的数值?分别是多少?
(3)取出的
3
张卡片上的数字之和是偶数的概率为多少?
答案
1.D
2.B
3.B
4.A
5.
B
6.
7.
8.
画树状图如图:
共有
9
个等可能的结果,小新同学两次摸出小球上的汉字相同的结果有
5
个,
∴小新同学两次摸出小球上的汉字相同的概率为.
9.
根据题意,列表如下:
由上表可以看出,所有可能的情况有
16
种,它们出现的可能性相等.
(1)两次摸出的纸牌上数字之和为
5(记为事件
A)的情况有
4
种,∴P(A)==.
(2)这个游戏公平.理由如下:
∵两次摸出的纸牌上数字之和为奇数(记为事件
B)的情况有
8
种,∴P(B)==,
两次摸出的纸牌上数字之和为偶数(记为事件
C)的情况有
8
种,∴P(C)==,
∴两次摸出的纸牌上数字之和为奇数与数字之和为偶数的概率相同,∴这个游戏公平.
10.
(1)画树状图如图:
由树状图知,共有
12
种等可能的结果,其中
3
个数都是偶数的结果有
2
种,所以
3
个数都是偶数的概率为=.
(2)取出的
3
张卡片上的数字之和共有
5
种不同的数值,分别是
13,14,15,16,17.
(3)共有
12
种等可能的结果,其中和为偶数的结果有
6
种,所以取出的
3
张卡片上的数字之和是偶数的概率为=.
5
用树状图或表格求概率(1)
1、甲、乙、丙三人站成一排拍照,则甲站在中间的概率是(
)
A.
B.
C.
D.
2、有三张正面分别写有数字-2,1,3
的卡片,它们的背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为
a
的值,然后把这张卡片放回去,洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为
b
的值,则点(a,b)在第一象限内的概率为(
)
A.
B.
C.
D.
3、小明和小亮在玩“石头、剪刀、布”的游戏,则两人一起做同样手势的概率是(
)
A.
B.
C.
D.
4、小蕾有某文学名著上、中、下各
1
册,她随机将它们叠放在一起,从上到下的顺序恰好为“上册、中册、下册”的概率是
.
5、从
1、2、3
中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的
数字,那么组成的两位数是
4
的倍数的概率是
.
6、从-2,-1,2
这三个数中任取两个不同的数相乘,则积为正数的概率是
.
7、三张反面完全相同的卡片,正面分别写有“木”“寸”“木”,把它们洗匀后,反面朝上,任取两张,能拼成“村”字的概率是
.
8、在一个箱内装入只有标号不同的三颗小球,标号分别为
1,2,3.每次随机取出一颗小球,记下标号作为得分,再将小球放回箱内.小明现已取球三次,得分分别为1
分,3
分,2
分,小明又从箱内取球两次,若五次得分的平均数不小于
2.2
分,请用画树状图或列表的方法,求发生“五次取球得分的平均数不小于
2.2
分”情况的概率.
9、有甲、乙两个不透明的布袋,甲袋中只装有
3
个除标号外完全相同的小球,分别标有数字0,1,2;乙袋中只装有
3
个除标号外完全相同的小球,分别标有数字-1,-2,0.现从甲袋中随机抽取一个小球,记录标有的数字为
x,再从乙袋中随机抽取一个小球,记录标有的数字为
y,由此确定点
M
的坐标为(x,y).
(1)写出点
M
所有可能的坐标;
(2)求点
M(x,y)在函数
y=-x+1
的图象上的概率.
答案
1.B
2.D
3.B
4.
5.
6.
7.
8.画树状图如下:
共有
9
种等可能的情况,由于五次得分的平均数不小于
2.2
分,所以五次的总得分不小于
11
分,所以后
2
次的得分不小于
5
分,在这
9
种情况中,不小于
5
分的情况有
3
种,所以发生“五次取球得分的平均数不小于
2.2
分”情况的概率为=.
9.
(1)列表如下:
(2)由(1)知,共有
9
种等可能的结果,满足点
M(x,y)在函数
y=-x+1
的图象上的结果有
2
个,即(2,-1),(1,0),所以点
M(x,y)在函数
y=-x+1
的图象上的概率为.
第1节
用树状图或表格求概率(2)
1、如图,两个转盘(每个转盘被分成面积相等的
4
个扇形)分别自由转动一次,当停止转动时,两个转盘的指针都指向
2
的概率为(
)
A.
B.
C.
D.
2、经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种情况的可能性大小相同,则事件“两辆车向右转,一辆车向左转”的概率为(
)
A.
B.
C.
D.
3、假定鸟卵孵化后,雏鸟为雌与雄的概率相同.若三枚卵全部成功孵化,则三只雏鸟中恰有两只雄鸟的概率是(
)
A.
B.
C.
D.
4、5
月
19
日为中国旅游日,某市推出旅游惠民活动,市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个景点游玩;下午从江郎山、三衢石林、开化根博园中随机选择一个景点游玩,则王先生恰好上午选中孔氏南宗家庙,下午选中江郎山的概率是(
)
A.
B.
C.
D.
5、某校甲、乙、丙、丁四名同学在运动会上参加
4×100
米接力比赛,其中甲跑第一棒,乙跑第二棒的概率是(
)
A.
B.
C.
D.
6、一个不透明的布袋中仅有
2
个红球,1
个黑球,这些球除颜色外无其他差别,先随机摸出一个小球,记下颜色后放回搅匀,再随机摸出一个小球,则两次摸出的小球颜色不同的概率是
.
7、如图,
随机闭合开关
S1,S2,S3
中的两个,能让灯泡发光的概率
是.
8、一个不透明的口袋中有三个小球,每个小球上只标有一个汉字,分别是“家”“家”“乐”,除汉字外其余均相同.小新同学从口袋中随机摸出一个小球,记下汉字后放回并搅匀;再从口袋中随机摸出一个小球记下汉字.用画树状图(或列表)的方法,求小新同学两次摸出小球上的汉字相同的概率.
9、在一个不透明的口袋中装有
4
张纸牌,纸牌上分别标有数字
1,2,3,4,除数字外其余均相同.洗匀后,随机摸出一张纸牌,然后放回,洗匀,再随机摸出一张纸牌.
(1)计算两次摸出的纸牌上数字之和为
5
的概率;
(2)甲、乙两个人进行游戏,若两次摸出的纸牌上数字之和为奇数,则甲胜;若两次摸出的纸牌上数字之和为偶数,则乙胜.这个游戏公平吗?请说明理由.
10、甲口袋中装有
2
张相同的卡片,它们分别写有数字
2
和
3;乙口袋中装有
3
张相同的卡片,它们分别写有数字
4,5
和
6;丙口袋中装有
2
张相同的卡片,它们分别写有数字
7
和
8.从三个口袋中各随机取出
1
张卡片.
(1)取出的
3
张卡片中,恰好
3
个数都是偶数的概率是多少?
(2)取出的
3
张卡片上的数字之和共有几种不同的数值?分别是多少?
(3)取出的
3
张卡片上的数字之和是偶数的概率为多少?
答案
1.D
2.B
3.B
4.A
5.
B
6.
7.
8.
画树状图如图:
共有
9
个等可能的结果,小新同学两次摸出小球上的汉字相同的结果有
5
个,
∴小新同学两次摸出小球上的汉字相同的概率为.
9.
根据题意,列表如下:
由上表可以看出,所有可能的情况有
16
种,它们出现的可能性相等.
(1)两次摸出的纸牌上数字之和为
5(记为事件
A)的情况有
4
种,∴P(A)==.
(2)这个游戏公平.理由如下:
∵两次摸出的纸牌上数字之和为奇数(记为事件
B)的情况有
8
种,∴P(B)==,
两次摸出的纸牌上数字之和为偶数(记为事件
C)的情况有
8
种,∴P(C)==,
∴两次摸出的纸牌上数字之和为奇数与数字之和为偶数的概率相同,∴这个游戏公平.
10.
(1)画树状图如图:
由树状图知,共有
12
种等可能的结果,其中
3
个数都是偶数的结果有
2
种,所以
3
个数都是偶数的概率为=.
(2)取出的
3
张卡片上的数字之和共有
5
种不同的数值,分别是
13,14,15,16,17.
(3)共有
12
种等可能的结果,其中和为偶数的结果有
6
种,所以取出的
3
张卡片上的数字之和是偶数的概率为=.
5
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
