人教版数学八年级上册一课一练12.2 全等三角形的判定(Word版含解析)
文档属性
| 名称 | 人教版数学八年级上册一课一练12.2 全等三角形的判定(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 10:08:05 | ||
图片预览


文档简介
12.2
全等三角形的判定
一、选择题(共15小题;共75分)
1.
和
中,若
,,.则
A.
B.
C.
D.
3.
阅读下面材料:
已知
,,,,线段
,
如图所示,
求作:,使得斜边
,一条直角边
.
作法:
(1)作射线
,,且
.
(2)以
点
为圆心,线段
长为半径作弧,交射线
于点
.
(3)以
点
为圆心,线段
长为半径作弧,交射线
于点
.
4)连接
.则
.
上述尺规作图过程中,用到的判定三角形全等的依据是
A.
B.
C.
D.
4.
如右上图,已知
,那么添加下列一个条件后,仍无法判定
的是
A.
B.
C.
D.
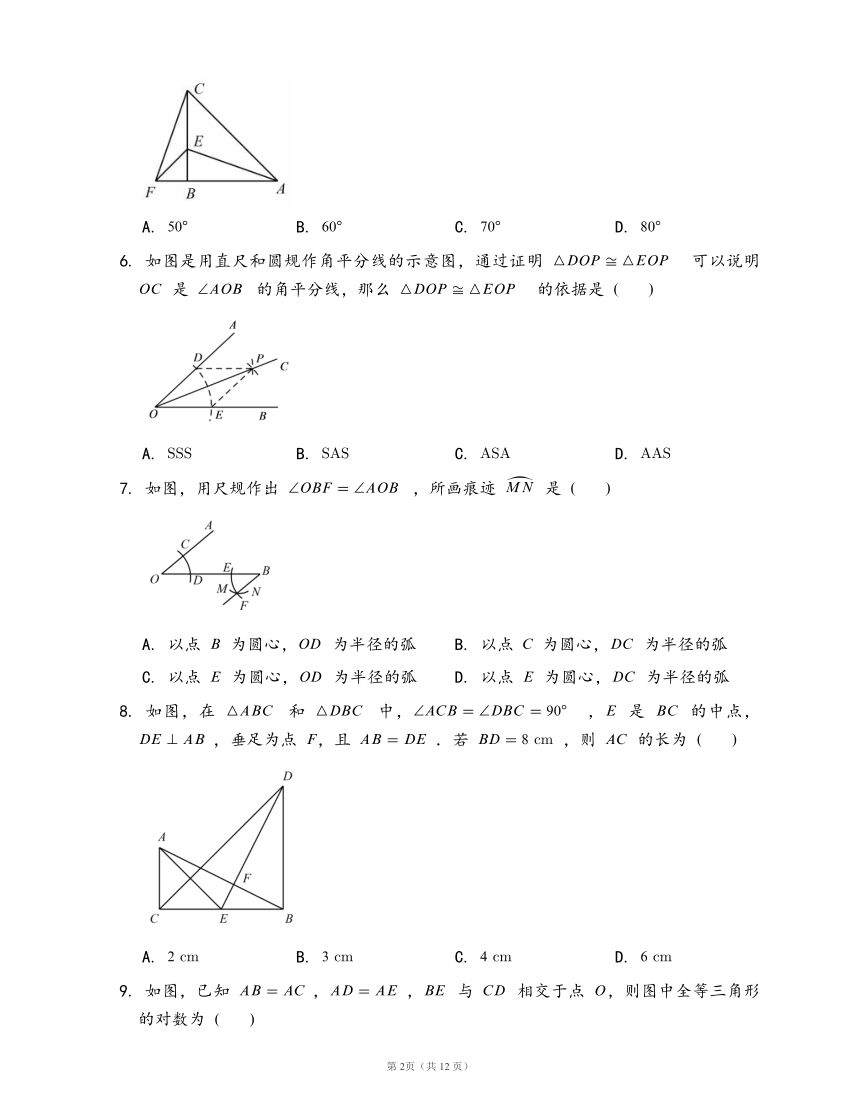
5.
如图,在
中,,,
为
延长线上一点,点
在
上,且
.若
,则
度数是
A.
B.
C.
D.
6.
如图是用直尺和圆规作角平分线的示意图,通过证明
可以说明
是
的角平分线,那么
的依据是
A.
B.
C.
D.
7.
如图,用尺规作出
,所画痕迹
是
A.
以点
为圆心,
为半径的弧
B.
以点
为圆心,
为半径的弧
C.
以点
为圆心,
为半径的弧
D.
以点
为圆心,
为半径的弧
8.
如图,在
和
中,,
是
的中点,,垂足为点
,且
.若
,则
的长为
A.
B.
C.
D.
9.
如图,已知
,,
与
相交于点
,则图中全等三角形的对数为
A.
B.
C.
D.
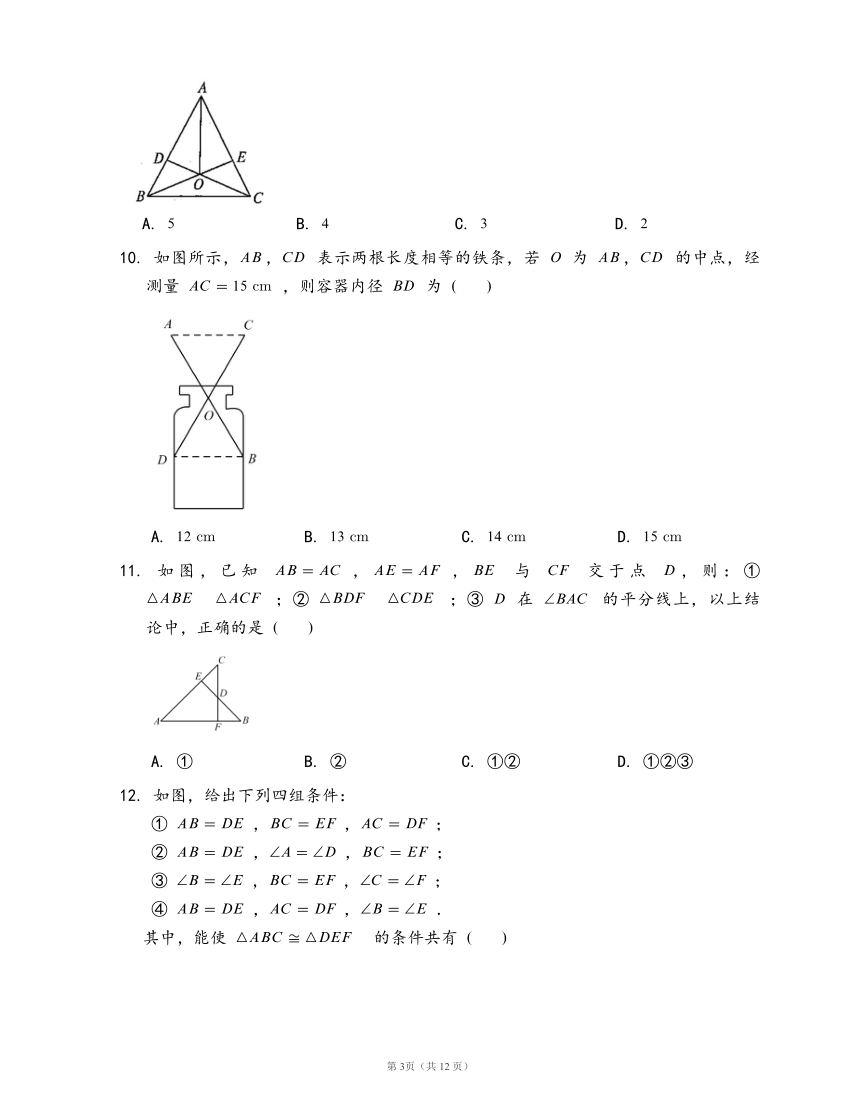
10.
如图所示,,
表示两根长度相等的铁条,若
为
,
的中点,经测量
,则容器内径
为
A.
B.
C.
D.
11.
如图,已知
,,
与
交于点
,则:①
;②
;③
在
的平分线上,以上结论中,正确的是
A.
①
B.
②
C.
①②
D.
①②③
12.
如图,给出下列四组条件:
①
,,;
②
,,;
③
,,;
④
,,.
其中,能使
的条件共有
A.
组
B.
组
C.
组
D.
组
13.
如图,用尺规作图作
的第一步是以点
为圆心,以任意长为半径画弧
①,分别交
,
于点
,,那么第二步的作图痕迹②的作法是
A.
以点
为圆心,
长为半径画弧
B.
以点
为圆心,
长为半径画弧
C.
以点
为圆心,
长为半径画弧
D.
以点
为圆心,
长为半径画弧
14.
如图,在
和
中,,,,.连接
,
交于点
,连接
.下列结论:
①
;②
;③
平分
;④
平分
其中正确的结论个数有
个.
A.
B.
C.
D.
15.
如图,
于
点
,
于
点
,若
,则下列结论中不正确的是
A.
B.
C.
D.
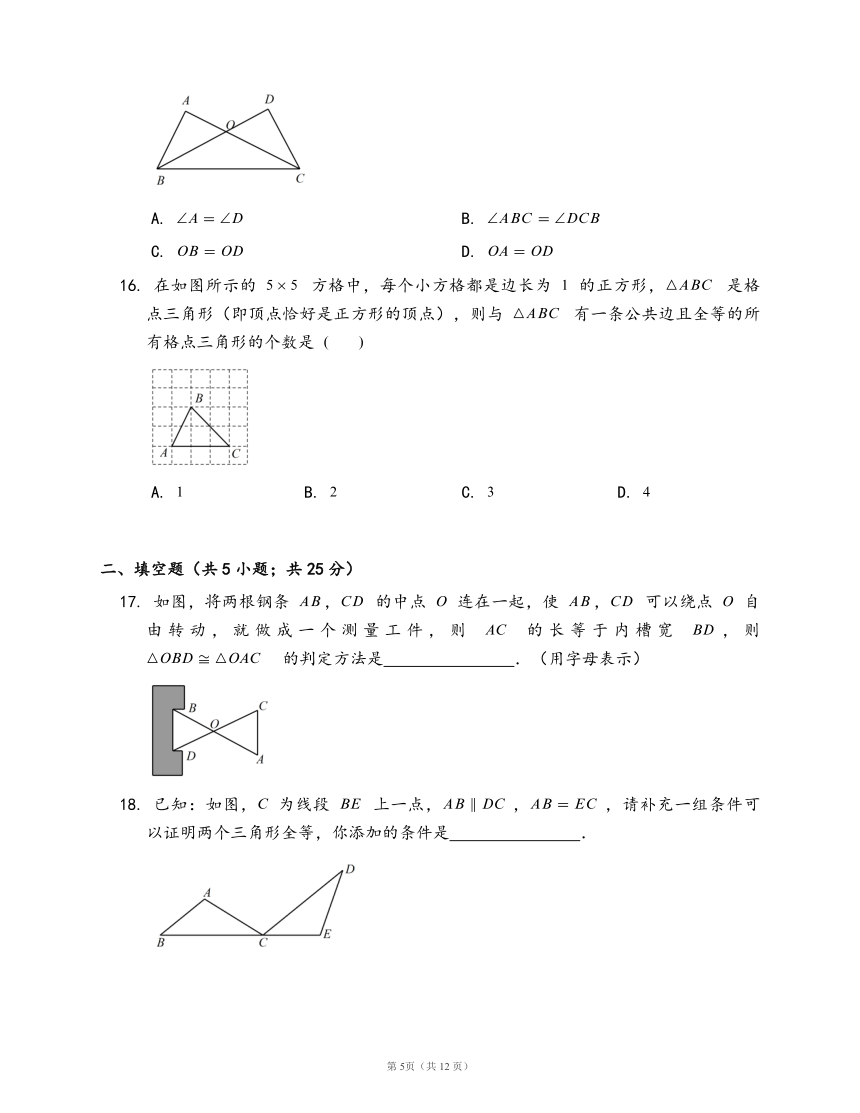
16.
在如图所示的
方格中,每个小方格都是边长为
的正方形,
是格点三角形(即顶点恰好是正方形的顶点),则与
有一条公共边且全等的所有格点三角形的个数是
A.
B.
C.
D.
二、填空题(共5小题;共25分)
17.
如图,将两根钢条
,
的中点
连在一起,使
,
可以绕点
自由转动,就做成一个测量工件,则
的长等于内槽宽
,则
的判定方法是
?.(用字母表示)
18.
已知:如图,
为线段
上一点,,,请补充一组条件可以证明两个三角形全等,你添加的条件是
?.
19.
如图,在
中,,,
于点
,
于点
,若
,,则
?
.
20.
如图,四边形
中,,,,
.
则
的大小
?
.
21.
阅读下面材料:
在数学课上,老师提出如下问题:
小芸的作图步骤如下:
老师说:“小芸的作图步骤正确,且可以得到
”.
请回答:得到
的依据是
?.
三、解答题(共3小题;共45分)
22.
如图,已知
,,,则
.请说明理由.
解:,
?
?,
即
?.
在
和
中,
(
?),
(
?).
23.
如图,已知
平分
,,若
是钝角,求证:.
24.
如图所示,已知
,,.求证:.
答案
第一部分
1.
B
【解析】注意对应顶点写在相应的位置.
3.
A
4.
C
5.
C
【解析】,
,
在
和
中,
.
,,
,
,
,
,
,
,故C选项正确.
6.
A
7.
D
8.
C
【解析】
.
9.
A
10.
D
11.
D
【解析】由题意可知:
.
,
.
.
,,
.
.
.
连接
.
,
,
.
.
点
在
的平分线上.
12.
B
【解析】条件①③均可判断
.
13.
D
14.
B
【解析】,
,
即
,
在
和
中,
,
,,②正确;
,
由三角形的外角性质得:,
,②正确;
作
于
,
于
,如图所示:
则
,
在
和
中,
,
,
平分
,④正确;
,
当
时,
才平分
,
假设
,
,
,
平分
,
,
在
和
中,
,
,
,
,
与
矛盾,
③错误;
正确的有①②④;
故选B.
15.
C
16.
D
第二部分
17.
18.
(答案不唯一)
19.
【解析】,
于点
,
于点
,
,.
.
在
和
中,
,
,,
,
,
,,
.
20.
21.
斜边、直角边(),全等三角形对应边相等.
第三部分
22.
;;;
已知;;已知;;;全等三角形的对应边相等
23.
如答图,过点
作
于点
,
交
的延长线于点
.
在
与
中,
,
.
,
,
又
,
.
在
与
中,
,
.
24.
,
.
,,
.
第12页(共12
页)
全等三角形的判定
一、选择题(共15小题;共75分)
1.
和
中,若
,,.则
A.
B.
C.
D.
3.
阅读下面材料:
已知
,,,,线段
,
如图所示,
求作:,使得斜边
,一条直角边
.
作法:
(1)作射线
,,且
.
(2)以
点
为圆心,线段
长为半径作弧,交射线
于点
.
(3)以
点
为圆心,线段
长为半径作弧,交射线
于点
.
4)连接
.则
.
上述尺规作图过程中,用到的判定三角形全等的依据是
A.
B.
C.
D.
4.
如右上图,已知
,那么添加下列一个条件后,仍无法判定
的是
A.
B.
C.
D.
5.
如图,在
中,,,
为
延长线上一点,点
在
上,且
.若
,则
度数是
A.
B.
C.
D.
6.
如图是用直尺和圆规作角平分线的示意图,通过证明
可以说明
是
的角平分线,那么
的依据是
A.
B.
C.
D.
7.
如图,用尺规作出
,所画痕迹
是
A.
以点
为圆心,
为半径的弧
B.
以点
为圆心,
为半径的弧
C.
以点
为圆心,
为半径的弧
D.
以点
为圆心,
为半径的弧
8.
如图,在
和
中,,
是
的中点,,垂足为点
,且
.若
,则
的长为
A.
B.
C.
D.
9.
如图,已知
,,
与
相交于点
,则图中全等三角形的对数为
A.
B.
C.
D.
10.
如图所示,,
表示两根长度相等的铁条,若
为
,
的中点,经测量
,则容器内径
为
A.
B.
C.
D.
11.
如图,已知
,,
与
交于点
,则:①
;②
;③
在
的平分线上,以上结论中,正确的是
A.
①
B.
②
C.
①②
D.
①②③
12.
如图,给出下列四组条件:
①
,,;
②
,,;
③
,,;
④
,,.
其中,能使
的条件共有
A.
组
B.
组
C.
组
D.
组
13.
如图,用尺规作图作
的第一步是以点
为圆心,以任意长为半径画弧
①,分别交
,
于点
,,那么第二步的作图痕迹②的作法是
A.
以点
为圆心,
长为半径画弧
B.
以点
为圆心,
长为半径画弧
C.
以点
为圆心,
长为半径画弧
D.
以点
为圆心,
长为半径画弧
14.
如图,在
和
中,,,,.连接
,
交于点
,连接
.下列结论:
①
;②
;③
平分
;④
平分
其中正确的结论个数有
个.
A.
B.
C.
D.
15.
如图,
于
点
,
于
点
,若
,则下列结论中不正确的是
A.
B.
C.
D.
16.
在如图所示的
方格中,每个小方格都是边长为
的正方形,
是格点三角形(即顶点恰好是正方形的顶点),则与
有一条公共边且全等的所有格点三角形的个数是
A.
B.
C.
D.
二、填空题(共5小题;共25分)
17.
如图,将两根钢条
,
的中点
连在一起,使
,
可以绕点
自由转动,就做成一个测量工件,则
的长等于内槽宽
,则
的判定方法是
?.(用字母表示)
18.
已知:如图,
为线段
上一点,,,请补充一组条件可以证明两个三角形全等,你添加的条件是
?.
19.
如图,在
中,,,
于点
,
于点
,若
,,则
?
.
20.
如图,四边形
中,,,,
.
则
的大小
?
.
21.
阅读下面材料:
在数学课上,老师提出如下问题:
小芸的作图步骤如下:
老师说:“小芸的作图步骤正确,且可以得到
”.
请回答:得到
的依据是
?.
三、解答题(共3小题;共45分)
22.
如图,已知
,,,则
.请说明理由.
解:,
?
?,
即
?.
在
和
中,
(
?),
(
?).
23.
如图,已知
平分
,,若
是钝角,求证:.
24.
如图所示,已知
,,.求证:.
答案
第一部分
1.
B
【解析】注意对应顶点写在相应的位置.
3.
A
4.
C
5.
C
【解析】,
,
在
和
中,
.
,,
,
,
,
,
,
,故C选项正确.
6.
A
7.
D
8.
C
【解析】
.
9.
A
10.
D
11.
D
【解析】由题意可知:
.
,
.
.
,,
.
.
.
连接
.
,
,
.
.
点
在
的平分线上.
12.
B
【解析】条件①③均可判断
.
13.
D
14.
B
【解析】,
,
即
,
在
和
中,
,
,,②正确;
,
由三角形的外角性质得:,
,②正确;
作
于
,
于
,如图所示:
则
,
在
和
中,
,
,
平分
,④正确;
,
当
时,
才平分
,
假设
,
,
,
平分
,
,
在
和
中,
,
,
,
,
与
矛盾,
③错误;
正确的有①②④;
故选B.
15.
C
16.
D
第二部分
17.
18.
(答案不唯一)
19.
【解析】,
于点
,
于点
,
,.
.
在
和
中,
,
,,
,
,
,,
.
20.
21.
斜边、直角边(),全等三角形对应边相等.
第三部分
22.
;;;
已知;;已知;;;全等三角形的对应边相等
23.
如答图,过点
作
于点
,
交
的延长线于点
.
在
与
中,
,
.
,
,
又
,
.
在
与
中,
,
.
24.
,
.
,,
.
第12页(共12
页)
