人教版数学八年级上册 12.3 角的平分线性质的应用 教案
文档属性
| 名称 | 人教版数学八年级上册 12.3 角的平分线性质的应用 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 236.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 23:05:02 | ||
图片预览


文档简介
12.3 角的平分线的性质(2)
一、教学目标
(一)知识与技能
1.了解角的平分线的判定定理;
2.会利用角的平分线的判定进行证明解决问题.
(二)过程与方法
在探究角的平分线的判定定理的过程中,进一步发展学生的推理 证明意识和能力.
(三)情感、态度与价值观
在探究作角的平分线的判定定理的过程中,培养学生探究问题的兴趣、合作交流的意识、动手操作的能力与探索精神,增强解决问题的信心,获得解决问题的成功体验.
二、教学重点、难点
重点:角的平分线的判定定理的证明及应用;
难点:角的平分线的判定.
三、教法学法
引导发现、讲练结合法.
四、教学过程
(一) 复习、回顾
1. 角平分线的性质:角的平分线上的点到角的两边的距离相等.
几何表达:(角的平分线上的点到角的两边的距离相等)
如图所示,∵OP平分∠AOB),PD⊥AO,PE⊥OB,
∴PD=PE.
(二)合作探究
角平分线的判定:在角的内部,到角的两边的距离相等的点在角的平分线上.(证明几何命题时的步骤:1、明确命题中的已知和求证。2、根据题意画出图形,并用符号表示已知和求证。3、经过分析,找出由已知推出要证的途径,写出证明过程。)
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上
证明: 经过点P作射线OC
∵ PD⊥OA,PE⊥OB
∴ ∠PDO=∠PEO=90°
在Rt△PDO和Rt△PEO中
PO=PO
PD=PE
∴ Rt△PDO≌Rt△PEO(HL)
∴ ∠ POD=∠POE
∴点P在∠AOB的平分线上
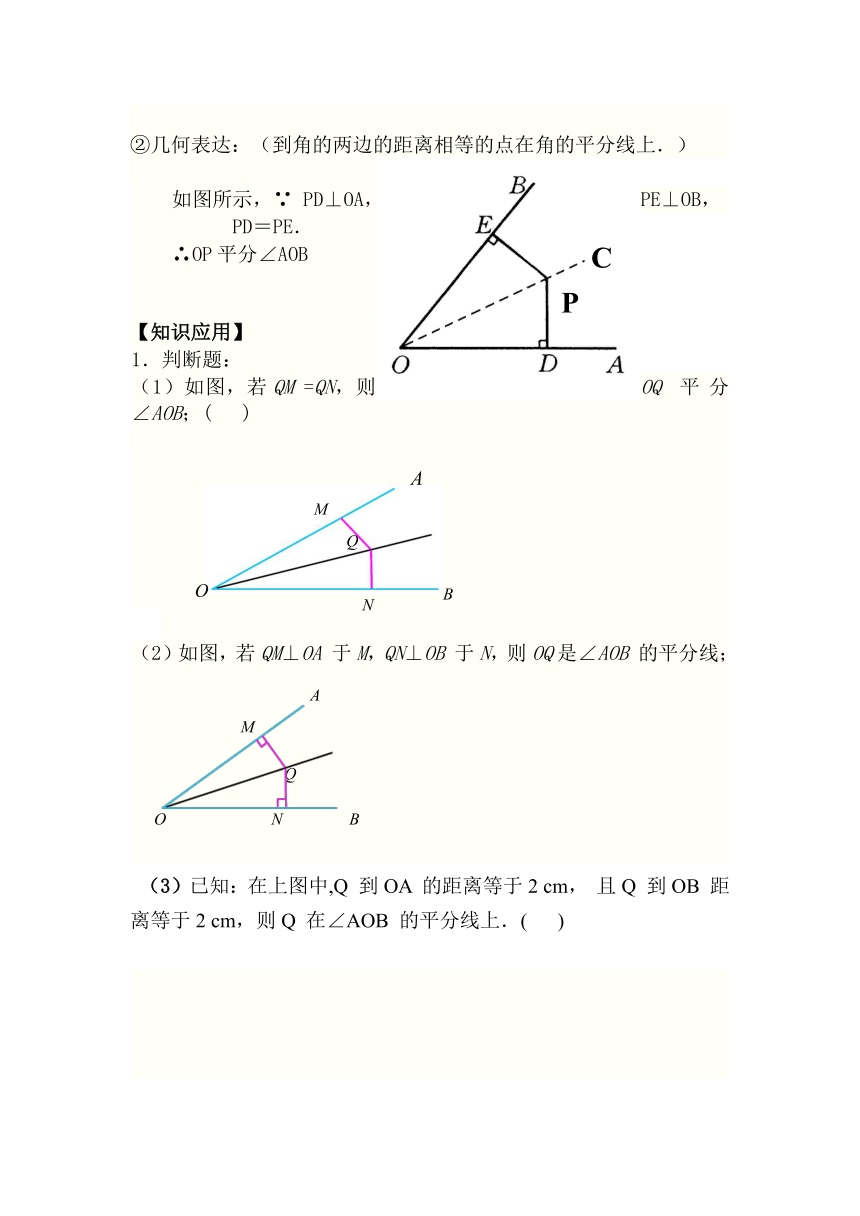
②几何表达:(到角的两边的距离相等的点在角的平分线上.)
如图所示,∵ PD⊥OA,PE⊥OB,
PD=PE.
∴OP平分∠AOB
【知识应用】
1.判断题:
(1)如图,若QM =QN,则OQ 平分∠AOB;( )
(2)如图,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的平分线;
(3)已知:在上图中,Q 到OA 的距离等于2 cm, 且Q 到OB 距离等于2 cm,则Q 在∠AOB 的平分线上.( )
2、例. 如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等
分析:由题中条件可知,本题可以采用角的平分线的判定来解答,因此要作出点P到三边的垂线段.
解:AP平分∠BAC.
结论:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等.
理由:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
∵BM是△ABC的角平分线且点P在BM上,
∴PD=PE(角平分线上的点到角的两边的距离相等).
同理PF=PE,∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
?想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等
3、 归纳 比较
注意上述两者中的条件和结论
条件中的理由有三个,必须写完全,不能少了任何一个。
性质和判定中的已知条件和结论的异同
(三)巩固训练
3. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
四、小结
1、角平分线的判定:
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上。
2、三角形角平分线的交点性质:
三角形的三条角平分线交于一点。
五、作业
习题12.3 3、7
六、教学反思:
本节课的教学目标是了解角的平分线的判定定理和会利用角的平分线的判定进行证明解决问题。教学过程分为三个环节,第一,跟着老师一起回顾知识,并引出课题;第二,探索新知,通过猜想、验证,总结角平分线的判定;第三,巩固新知。在教学中我采用了体验探究的教学方式,在教师配合引导下,让学生自己动手、动脑、操作、观察、归纳出角平分性的判定,体验知识的形成过程,力求体现“主题参与、自主探索、合作交流、指导引探”的教学理念。
一、教学目标
(一)知识与技能
1.了解角的平分线的判定定理;
2.会利用角的平分线的判定进行证明解决问题.
(二)过程与方法
在探究角的平分线的判定定理的过程中,进一步发展学生的推理 证明意识和能力.
(三)情感、态度与价值观
在探究作角的平分线的判定定理的过程中,培养学生探究问题的兴趣、合作交流的意识、动手操作的能力与探索精神,增强解决问题的信心,获得解决问题的成功体验.
二、教学重点、难点
重点:角的平分线的判定定理的证明及应用;
难点:角的平分线的判定.
三、教法学法
引导发现、讲练结合法.
四、教学过程
(一) 复习、回顾
1. 角平分线的性质:角的平分线上的点到角的两边的距离相等.
几何表达:(角的平分线上的点到角的两边的距离相等)
如图所示,∵OP平分∠AOB),PD⊥AO,PE⊥OB,
∴PD=PE.
(二)合作探究
角平分线的判定:在角的内部,到角的两边的距离相等的点在角的平分线上.(证明几何命题时的步骤:1、明确命题中的已知和求证。2、根据题意画出图形,并用符号表示已知和求证。3、经过分析,找出由已知推出要证的途径,写出证明过程。)
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上
证明: 经过点P作射线OC
∵ PD⊥OA,PE⊥OB
∴ ∠PDO=∠PEO=90°
在Rt△PDO和Rt△PEO中
PO=PO
PD=PE
∴ Rt△PDO≌Rt△PEO(HL)
∴ ∠ POD=∠POE
∴点P在∠AOB的平分线上
②几何表达:(到角的两边的距离相等的点在角的平分线上.)
如图所示,∵ PD⊥OA,PE⊥OB,
PD=PE.
∴OP平分∠AOB
【知识应用】
1.判断题:
(1)如图,若QM =QN,则OQ 平分∠AOB;( )
(2)如图,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的平分线;
(3)已知:在上图中,Q 到OA 的距离等于2 cm, 且Q 到OB 距离等于2 cm,则Q 在∠AOB 的平分线上.( )
2、例. 如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等
分析:由题中条件可知,本题可以采用角的平分线的判定来解答,因此要作出点P到三边的垂线段.
解:AP平分∠BAC.
结论:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等.
理由:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
∵BM是△ABC的角平分线且点P在BM上,
∴PD=PE(角平分线上的点到角的两边的距离相等).
同理PF=PE,∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
?想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等
3、 归纳 比较
注意上述两者中的条件和结论
条件中的理由有三个,必须写完全,不能少了任何一个。
性质和判定中的已知条件和结论的异同
(三)巩固训练
3. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
四、小结
1、角平分线的判定:
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上。
2、三角形角平分线的交点性质:
三角形的三条角平分线交于一点。
五、作业
习题12.3 3、7
六、教学反思:
本节课的教学目标是了解角的平分线的判定定理和会利用角的平分线的判定进行证明解决问题。教学过程分为三个环节,第一,跟着老师一起回顾知识,并引出课题;第二,探索新知,通过猜想、验证,总结角平分线的判定;第三,巩固新知。在教学中我采用了体验探究的教学方式,在教师配合引导下,让学生自己动手、动脑、操作、观察、归纳出角平分性的判定,体验知识的形成过程,力求体现“主题参与、自主探索、合作交流、指导引探”的教学理念。
