人教版数学八年级上册12.3 探究角平分线的性质教案(习题无答案)
文档属性
| 名称 | 人教版数学八年级上册12.3 探究角平分线的性质教案(习题无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 83.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 00:00:00 | ||
图片预览

文档简介
角平分线的性质
教学设计
【教学内容】义务教育人教版第八年级上册12.3《角平分线的性质》
1、教学内容分析
本节课是在七年级学习了角平分线的概念、点到直线的距离和前面刚学完证明三角形全等的基础上进行教学的.内容包括角平分线的作法、角平分线的性质及初步应用.其中:
A、作角的平分线是基本作图;
B、角平分线的性质为证明线段或角相等开辟了新的途径,又为后面角平分线的判定定理的学习奠定了基础.因此,本节内容在数学知识体系中起到了承上启下的作用.
2、学情分析
刚进入初二的学生观察、操作、猜想能力较强,但归纳、运用数学意识的思想比较薄弱,思维的广阔性、敏捷性、灵活性比较欠缺,需要在课堂教学中进一步加强培养.
【教学目标】
一、知识与技能
1、掌握用尺规作已知角的平分线的方法.
2、理解角的平分线的性质并能初步运用.
二、过程与方法
通过让学生经历观察演示,动手操作,合作交流,自主探究等过程,培养学生用数学知识解决问题的能力.
三、情感、态度、价值观
培养学生探究问题的兴趣,增强解决问题的信心,激发学生应用数学的热情.
【教学重点】
1、掌握角平分线的尺规作图;
2、理解角的平分线的性质并能初步运用.
【教学难点】
理解角平分线性质及作法
【教学方法】本节课采用引导发现法、主动探究法、讲授教学法,指导学生“动手操作,自主探究”.鼓励学生多思、多说、多练,坚持师生间的多向交流。
【教学手段】 多媒体课件、筷子分角器
【课 型】 新授课
【教学过程】
复习引入
说一说我们学习过的证明两个三角形全等的方法:
SSS 2、SAS
3、 AAS 4、ASA
2、教师点拨:也就是说要证明两个三角形全等,我们至少需要三个条件。
引导学生思考并判断:
(1)要证明两个三角形全等,其中必须有一个边相等的条件。( )
(2)要证明两个三角形全等,其中必须有一个角相等的条件。( )
二、新课教学
1、教师多媒体出示情景问题:
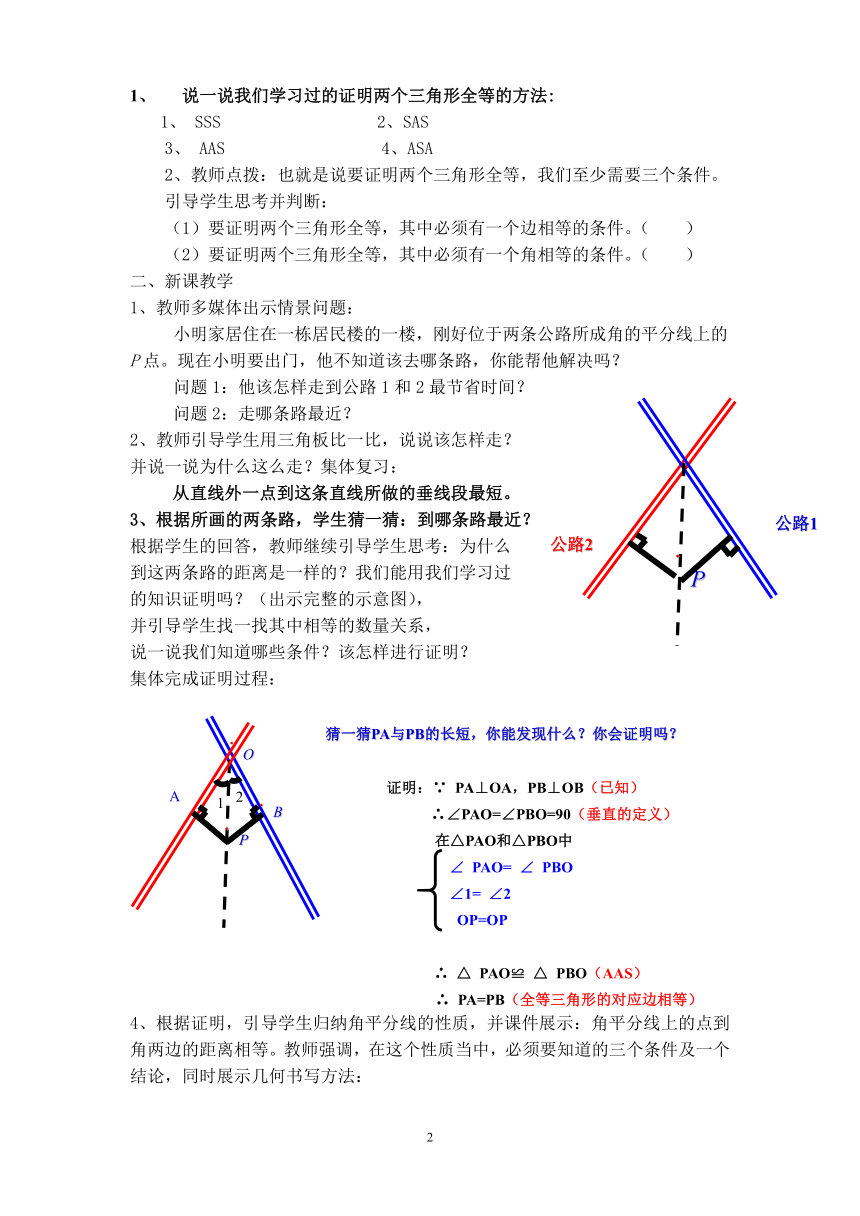
小明家居住在一栋居民楼的一楼,刚好位于两条公路所成角的平分线上的P点。现在小明要出门,他不知道该去哪条路,你能帮他解决吗?
问题1:他该怎样走到公路1和2最节省时间?
问题2:走哪条路最近?
2、教师引导学生用三角板比一比,说说该怎样走?
并说一说为什么这么走?集体复习:
从直线外一点到这条直线所做的垂线段最短。
3、根据所画的两条路,学生猜一猜:到哪条路最近?
根据学生的回答,教师继续引导学生思考:为什么
到这两条路的距离是一样的?我们能用我们学习过
的知识证明吗?(出示完整的示意图),
并引导学生找一找其中相等的数量关系,
说一说我们知道哪些条件?该怎样进行证明?
集体完成证明过程:
4、根据证明,引导学生归纳角平分线的性质,并课件展示:角平分线上的点到角两边的距离相等。教师强调,在这个性质当中,必须要知道的三个条件及一个结论,同时展示几何书写方法:
∵ ∠1= ∠2
PD ⊥OA 教师强调:三个条件缺一不可
PE ⊥OB
∴PD=PE(角的平分线上的点到角的两边的距离相等)
5、课堂小练习:判断对错
通过三个不同的练习,让学生进一步明确在
角平分线的性质当中,三个条件同等的
重要性。
6、动手操作,学生用撕纸的方法验证角平分线性质的准确性。
7角平分线的做法:
教师引导学生思考既然角平分线有这样的性质,那么我们如何做一个角的角平分线呢?点拨:只要你画出一个角,我就能做出其中的角平分线。学生画角后,教师利用筷子做的“分角器”画角的平分线,并引导学生观察“分角器”的特征:上面两条边长度相等,下面两条边长度相等,当它与角的边重合时,在这个角的两条边上所取得长度也相等,同时在角的两条边上的点到第四个顶点的距离也相等,想一想我们不用“分角器”该如何画一个角的平分线?
教师根据前面的分析画角的平分线,集体归纳角平分线的做法
⑴以角的顶点O为圆心,任意长为半径作弧,交OA于M,交OB于N.
⑵分别以M,N为圆心,大于 的长为半径作弧,两弧在∠AOB的内部交于点C.
⑶作射线OC,
射线OC即为∠AOB的角平分线.
8.集体证明这样做出的射线就是所做的角平分线:
三、巩固练习
如图,△ABC中, AD是∠BAC的平分线, ∠C=90°,DE⊥AB于E,BC=10,BD=4,求DE.
引导学生分析题目中的已知条件,猜一猜DE的长度会是多少?
想一想:DE的长度应该跟哪条边的长度一样?为什么?该
如何解决这个问题?
集体解答:
解: ∵ AD是∠BAC的平分线
AC⊥BC DE⊥AB
∴DE=CD=BC-BD
=10-4
=6
(角的平分线上的点到角的两边的距离相等)
四、课堂总结:
通过这节课的学习,你知道角平分线的性质了吗?该怎样画一个角的角平分线?
集体复习这节课所学的角平分线的性质,并简要口述角平分线的做法。
五、作业布置:
必做题:教材第50页第2题
选做题:教材第51页第2题
3
教学设计
【教学内容】义务教育人教版第八年级上册12.3《角平分线的性质》
1、教学内容分析
本节课是在七年级学习了角平分线的概念、点到直线的距离和前面刚学完证明三角形全等的基础上进行教学的.内容包括角平分线的作法、角平分线的性质及初步应用.其中:
A、作角的平分线是基本作图;
B、角平分线的性质为证明线段或角相等开辟了新的途径,又为后面角平分线的判定定理的学习奠定了基础.因此,本节内容在数学知识体系中起到了承上启下的作用.
2、学情分析
刚进入初二的学生观察、操作、猜想能力较强,但归纳、运用数学意识的思想比较薄弱,思维的广阔性、敏捷性、灵活性比较欠缺,需要在课堂教学中进一步加强培养.
【教学目标】
一、知识与技能
1、掌握用尺规作已知角的平分线的方法.
2、理解角的平分线的性质并能初步运用.
二、过程与方法
通过让学生经历观察演示,动手操作,合作交流,自主探究等过程,培养学生用数学知识解决问题的能力.
三、情感、态度、价值观
培养学生探究问题的兴趣,增强解决问题的信心,激发学生应用数学的热情.
【教学重点】
1、掌握角平分线的尺规作图;
2、理解角的平分线的性质并能初步运用.
【教学难点】
理解角平分线性质及作法
【教学方法】本节课采用引导发现法、主动探究法、讲授教学法,指导学生“动手操作,自主探究”.鼓励学生多思、多说、多练,坚持师生间的多向交流。
【教学手段】 多媒体课件、筷子分角器
【课 型】 新授课
【教学过程】
复习引入
说一说我们学习过的证明两个三角形全等的方法:
SSS 2、SAS
3、 AAS 4、ASA
2、教师点拨:也就是说要证明两个三角形全等,我们至少需要三个条件。
引导学生思考并判断:
(1)要证明两个三角形全等,其中必须有一个边相等的条件。( )
(2)要证明两个三角形全等,其中必须有一个角相等的条件。( )
二、新课教学
1、教师多媒体出示情景问题:
小明家居住在一栋居民楼的一楼,刚好位于两条公路所成角的平分线上的P点。现在小明要出门,他不知道该去哪条路,你能帮他解决吗?
问题1:他该怎样走到公路1和2最节省时间?
问题2:走哪条路最近?
2、教师引导学生用三角板比一比,说说该怎样走?
并说一说为什么这么走?集体复习:
从直线外一点到这条直线所做的垂线段最短。
3、根据所画的两条路,学生猜一猜:到哪条路最近?
根据学生的回答,教师继续引导学生思考:为什么
到这两条路的距离是一样的?我们能用我们学习过
的知识证明吗?(出示完整的示意图),
并引导学生找一找其中相等的数量关系,
说一说我们知道哪些条件?该怎样进行证明?
集体完成证明过程:
4、根据证明,引导学生归纳角平分线的性质,并课件展示:角平分线上的点到角两边的距离相等。教师强调,在这个性质当中,必须要知道的三个条件及一个结论,同时展示几何书写方法:
∵ ∠1= ∠2
PD ⊥OA 教师强调:三个条件缺一不可
PE ⊥OB
∴PD=PE(角的平分线上的点到角的两边的距离相等)
5、课堂小练习:判断对错
通过三个不同的练习,让学生进一步明确在
角平分线的性质当中,三个条件同等的
重要性。
6、动手操作,学生用撕纸的方法验证角平分线性质的准确性。
7角平分线的做法:
教师引导学生思考既然角平分线有这样的性质,那么我们如何做一个角的角平分线呢?点拨:只要你画出一个角,我就能做出其中的角平分线。学生画角后,教师利用筷子做的“分角器”画角的平分线,并引导学生观察“分角器”的特征:上面两条边长度相等,下面两条边长度相等,当它与角的边重合时,在这个角的两条边上所取得长度也相等,同时在角的两条边上的点到第四个顶点的距离也相等,想一想我们不用“分角器”该如何画一个角的平分线?
教师根据前面的分析画角的平分线,集体归纳角平分线的做法
⑴以角的顶点O为圆心,任意长为半径作弧,交OA于M,交OB于N.
⑵分别以M,N为圆心,大于 的长为半径作弧,两弧在∠AOB的内部交于点C.
⑶作射线OC,
射线OC即为∠AOB的角平分线.
8.集体证明这样做出的射线就是所做的角平分线:
三、巩固练习
如图,△ABC中, AD是∠BAC的平分线, ∠C=90°,DE⊥AB于E,BC=10,BD=4,求DE.
引导学生分析题目中的已知条件,猜一猜DE的长度会是多少?
想一想:DE的长度应该跟哪条边的长度一样?为什么?该
如何解决这个问题?
集体解答:
解: ∵ AD是∠BAC的平分线
AC⊥BC DE⊥AB
∴DE=CD=BC-BD
=10-4
=6
(角的平分线上的点到角的两边的距离相等)
四、课堂总结:
通过这节课的学习,你知道角平分线的性质了吗?该怎样画一个角的角平分线?
集体复习这节课所学的角平分线的性质,并简要口述角平分线的做法。
五、作业布置:
必做题:教材第50页第2题
选做题:教材第51页第2题
3
