人教版数学八年级上册同步检测12.2 全等三角形的判定(Word版含答案)
文档属性
| 名称 | 人教版数学八年级上册同步检测12.2 全等三角形的判定(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 10:46:52 | ||
图片预览




文档简介
12.2
全等三角形的判定
一、选择题(共16小题;共80分)
1.
如图,在
中,,,则可由“”直接判定的是
A.
B.
C.
D.
以上都不对
2.
如图,要测量河两岸相对的两点
,
的距离,先在
的垂线
上取两点
,,使
,再作出
的垂线
,使点
,,
在同一条直线上(如图所示),可以说明
,得
,因此测得
的长就是
的长,判定
,最恰当的理由是
A.
边角边
B.
角边角
C.
边边边
D.
边边角
3.
下列各条件中,不能作出唯一三角形的是
A.
已知两边和夹角
B.
已知两角和夹边
C.
已知两边和其中一边的对角
D.
已知三边
4.
如图是玩具拼图模板的一部分,已知
的六个元素,则下面甲、乙、丙三个三角形中能和
完全重合的是
A.
甲和丙
B.
丙和乙
C.
只有甲
D.
只有丙
5.
如图,点
,
在
上,,,,若
,则
等于
A.
B.
C.
D.
6.
如图所示,在
中,,,,则
的度数是
A.
B.
C.
D.
7.
已知
,则下列属于尺规作图的是
A.
用量角器画一个角等于
B.
用三角板画一个角等于
C.
用没有刻度的直尺通过目测画一个角等于
D.
用圆规和没有刻度的直尺画一个角等于
8.
如图
,
,
是锐角
的高,两高相交于点
,若
,,,则
的长为
A.
B.
C.
D.
9.
如图,在
中,
为
上一点,,
两点分别在
,
边上.若
,,,则
A.
B.
C.
D.
10.
如图所示,太阳光线
与
是平行的,
表示一颗塔松,
表示一颗小杨树,同一时刻两棵树的影长相等,已知小杨树高
米,则塔松高
A.
大于
米
B.
等于
米
C.
小于
米
D.
和影子的长相等
11.
如图,,若
,,则
的长为
A.
B.
C.
D.
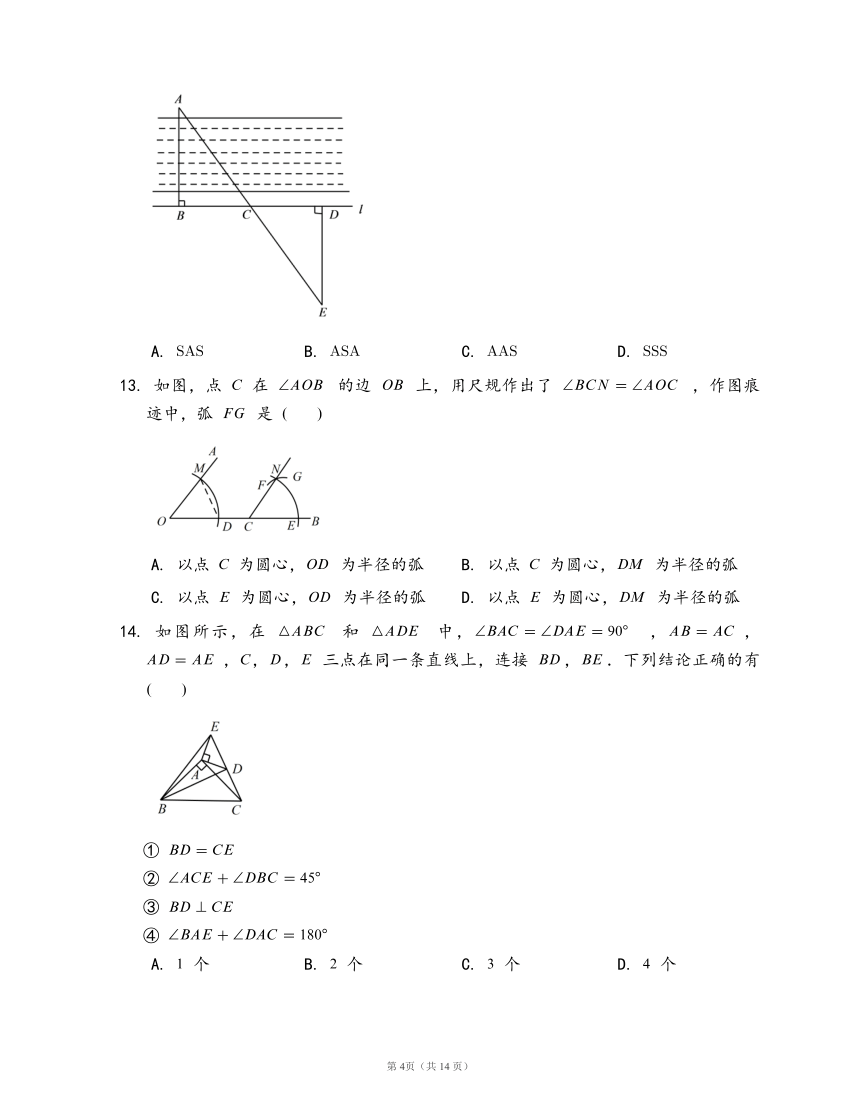
12.
如图,要测量河两岸相对的两点
、
间的距离,先在过点
的
的垂线
上取两点
、
,使
,再在过
的垂线上取点
,使
、
、
在一条直线上,这时
,.测得
的长就是
、
的距离,这里判断
的理由是
A.
B.
C.
D.
13.
如图,点
在
的边
上,用尺规作出了
,作图痕迹中,弧
是
A.
以点
为圆心,
为半径的弧
B.
以点
为圆心,
为半径的弧
C.
以点
为圆心,
为半径的弧
D.
以点
为圆心,
为半径的弧
14.
如图所示,在
和
中,,,,,,
三点在同一条直线上,连接
,.下列结论正确的有
①
②
③
④
A.
个
B.
个
C.
个
D.
个
15.
如图所示,点
是矩形
的边
延长线上的一点,且
,连接
交
于点
,连接
,下列结论不正确的是
A.
B.
C.
D.
16.
用直尺和圆规作一个角的平分线的示意图如图所示,则能说明
的依据是
A.
B.
C.
D.
角平分线上的点到角两边距离相等
二、填空题(共5小题;共25分)
17.
如图,要测量池塘的宽度
,在池塘外选取一点
,连接
,
并各自延长,使
,,连接
,测得
长为
,则池塘宽
为
?
,依据是
?.
18.
如图,在
中,,,
经过
点,且
,.若
,,则
?.
19.
如图,
是
的角平分线,,垂足为
,
交
的延长线于点
,若
恰好平分
,.给出下列四个结论:;;;.其中正确的结论的序号为
?.
20.
如图,
中,,,,直线
经过点
且与边
相交.动点
从点
出发沿
路径向终点
运动;动点
从点
出发沿
路径向终点
运动.点
和点
的速度分别为
和
,两点同时出发并开始计时,当点
到达终点
时计时结束.在某时刻分别过点
和点
作
于点
,
于点
,设运动时间为
秒,则当
?时,
与
全等.
21.
如图所示,,,垂足分别为
,,,,则
?
?
.
三、解答题(共3小题;共45分)
22.
如图,在
中,,,
过点
,,,垂足分别为点
,.求证:.
23.
是经过
顶点
的一条直线,.,
分别是直线
上两点,且
.
(1)若直线
经过
的内部,且
,
在射线
上,请解决下面两个问题:
①如图1,若
,,则
?
;
?
(填“”,“”或“”);
②如图2,若
,请添加一个关于
与
关系的条件
?,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线
经过
的外部,,请提出
,,
三条线段数量关系是合理猜想(不要求证明).
24.
已知
,
.求证:.
答案
第一部分
1.
B
2.
B
3.
C
4.
A
5.
C
6.
B
7.
D
【解析】因为用量角器可以量出一个角等于
,三角板中有一个角等于
,
因此A,B都不属于尺规作图;
因为通过目测画一个角等于
是不准确的,
所以C也不属于尺规作图;
只有D属于尺规作图.
8.
B
【解析】,
是锐角
的高,
.
.
又
,,
.
,.
,
.
.
9.
B
【解析】易证
.
.
,
,
.
10.
B
【解析】根据同一时刻的太阳光线是平行的,可得出
;然后根据塔松和小杨树都是垂直于地面且他们的影子相等,利用
可得
.
11.
A
12.
B
【解析】因为
,,
所以
,
在
和
中,
,
所以
13.
D
14.
D
【解析】①
,
.
即
.
在
和
中,
(),
.故①正确;
②
,,
.
.
,故②正确;
③
,
.
,
.
.
.
;故③正确;
④
,
.
15.
A
【解析】,,
为
的中位线,
,
在
和
中,
();
在
和
中,
();
,
;
故B、C、D均正确.
16.
A
第二部分
17.
,,全等三角形对应边相等
18.
【解析】,,
,
,,,
,.
在
和
中,
,
,.
,,,
.
19.
20.
或
或
秒
【解析】由题意得,,,
,,
,.
①如图
,当
时,
则
,即
,解得:;
②如图
,
点
与点
重合,
与
全等,则
,
,解得:;
③如图
,当点
与
重合时,,
则
,即
,解得:.
综上所述:当
秒或
秒或
秒时,
与
全等.
21.
,
第三部分
22.
略.
23.
(1)
①
;
②所填的条件是:.
证明:在
中,.
因为
,
所以
,
又因为
,
所以
,
又因为
,,
在
和
中,
所以
,
所以
,,
又因为
,
所以
.
【解析】①因为
,,
所以
,,
所以
,
因为
,;
在
和
中,
所以
,
所以
;.
??????(2)
猜想:.
【解析】证明过程:
因为
,,,,
所以
,
又因为
,
在
和
中,
所以
.
所以
,,
所以
.
24.
在
和
中,
,
,
,
,
即
.
第1页(共14
页)
全等三角形的判定
一、选择题(共16小题;共80分)
1.
如图,在
中,,,则可由“”直接判定的是
A.
B.
C.
D.
以上都不对
2.
如图,要测量河两岸相对的两点
,
的距离,先在
的垂线
上取两点
,,使
,再作出
的垂线
,使点
,,
在同一条直线上(如图所示),可以说明
,得
,因此测得
的长就是
的长,判定
,最恰当的理由是
A.
边角边
B.
角边角
C.
边边边
D.
边边角
3.
下列各条件中,不能作出唯一三角形的是
A.
已知两边和夹角
B.
已知两角和夹边
C.
已知两边和其中一边的对角
D.
已知三边
4.
如图是玩具拼图模板的一部分,已知
的六个元素,则下面甲、乙、丙三个三角形中能和
完全重合的是
A.
甲和丙
B.
丙和乙
C.
只有甲
D.
只有丙
5.
如图,点
,
在
上,,,,若
,则
等于
A.
B.
C.
D.
6.
如图所示,在
中,,,,则
的度数是
A.
B.
C.
D.
7.
已知
,则下列属于尺规作图的是
A.
用量角器画一个角等于
B.
用三角板画一个角等于
C.
用没有刻度的直尺通过目测画一个角等于
D.
用圆规和没有刻度的直尺画一个角等于
8.
如图
,
,
是锐角
的高,两高相交于点
,若
,,,则
的长为
A.
B.
C.
D.
9.
如图,在
中,
为
上一点,,
两点分别在
,
边上.若
,,,则
A.
B.
C.
D.
10.
如图所示,太阳光线
与
是平行的,
表示一颗塔松,
表示一颗小杨树,同一时刻两棵树的影长相等,已知小杨树高
米,则塔松高
A.
大于
米
B.
等于
米
C.
小于
米
D.
和影子的长相等
11.
如图,,若
,,则
的长为
A.
B.
C.
D.
12.
如图,要测量河两岸相对的两点
、
间的距离,先在过点
的
的垂线
上取两点
、
,使
,再在过
的垂线上取点
,使
、
、
在一条直线上,这时
,.测得
的长就是
、
的距离,这里判断
的理由是
A.
B.
C.
D.
13.
如图,点
在
的边
上,用尺规作出了
,作图痕迹中,弧
是
A.
以点
为圆心,
为半径的弧
B.
以点
为圆心,
为半径的弧
C.
以点
为圆心,
为半径的弧
D.
以点
为圆心,
为半径的弧
14.
如图所示,在
和
中,,,,,,
三点在同一条直线上,连接
,.下列结论正确的有
①
②
③
④
A.
个
B.
个
C.
个
D.
个
15.
如图所示,点
是矩形
的边
延长线上的一点,且
,连接
交
于点
,连接
,下列结论不正确的是
A.
B.
C.
D.
16.
用直尺和圆规作一个角的平分线的示意图如图所示,则能说明
的依据是
A.
B.
C.
D.
角平分线上的点到角两边距离相等
二、填空题(共5小题;共25分)
17.
如图,要测量池塘的宽度
,在池塘外选取一点
,连接
,
并各自延长,使
,,连接
,测得
长为
,则池塘宽
为
?
,依据是
?.
18.
如图,在
中,,,
经过
点,且
,.若
,,则
?.
19.
如图,
是
的角平分线,,垂足为
,
交
的延长线于点
,若
恰好平分
,.给出下列四个结论:;;;.其中正确的结论的序号为
?.
20.
如图,
中,,,,直线
经过点
且与边
相交.动点
从点
出发沿
路径向终点
运动;动点
从点
出发沿
路径向终点
运动.点
和点
的速度分别为
和
,两点同时出发并开始计时,当点
到达终点
时计时结束.在某时刻分别过点
和点
作
于点
,
于点
,设运动时间为
秒,则当
?时,
与
全等.
21.
如图所示,,,垂足分别为
,,,,则
?
?
.
三、解答题(共3小题;共45分)
22.
如图,在
中,,,
过点
,,,垂足分别为点
,.求证:.
23.
是经过
顶点
的一条直线,.,
分别是直线
上两点,且
.
(1)若直线
经过
的内部,且
,
在射线
上,请解决下面两个问题:
①如图1,若
,,则
?
;
?
(填“”,“”或“”);
②如图2,若
,请添加一个关于
与
关系的条件
?,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线
经过
的外部,,请提出
,,
三条线段数量关系是合理猜想(不要求证明).
24.
已知
,
.求证:.
答案
第一部分
1.
B
2.
B
3.
C
4.
A
5.
C
6.
B
7.
D
【解析】因为用量角器可以量出一个角等于
,三角板中有一个角等于
,
因此A,B都不属于尺规作图;
因为通过目测画一个角等于
是不准确的,
所以C也不属于尺规作图;
只有D属于尺规作图.
8.
B
【解析】,
是锐角
的高,
.
.
又
,,
.
,.
,
.
.
9.
B
【解析】易证
.
.
,
,
.
10.
B
【解析】根据同一时刻的太阳光线是平行的,可得出
;然后根据塔松和小杨树都是垂直于地面且他们的影子相等,利用
可得
.
11.
A
12.
B
【解析】因为
,,
所以
,
在
和
中,
,
所以
13.
D
14.
D
【解析】①
,
.
即
.
在
和
中,
(),
.故①正确;
②
,,
.
.
,故②正确;
③
,
.
,
.
.
.
;故③正确;
④
,
.
15.
A
【解析】,,
为
的中位线,
,
在
和
中,
();
在
和
中,
();
,
;
故B、C、D均正确.
16.
A
第二部分
17.
,,全等三角形对应边相等
18.
【解析】,,
,
,,,
,.
在
和
中,
,
,.
,,,
.
19.
20.
或
或
秒
【解析】由题意得,,,
,,
,.
①如图
,当
时,
则
,即
,解得:;
②如图
,
点
与点
重合,
与
全等,则
,
,解得:;
③如图
,当点
与
重合时,,
则
,即
,解得:.
综上所述:当
秒或
秒或
秒时,
与
全等.
21.
,
第三部分
22.
略.
23.
(1)
①
;
②所填的条件是:.
证明:在
中,.
因为
,
所以
,
又因为
,
所以
,
又因为
,,
在
和
中,
所以
,
所以
,,
又因为
,
所以
.
【解析】①因为
,,
所以
,,
所以
,
因为
,;
在
和
中,
所以
,
所以
;.
??????(2)
猜想:.
【解析】证明过程:
因为
,,,,
所以
,
又因为
,
在
和
中,
所以
.
所以
,,
所以
.
24.
在
和
中,
,
,
,
,
即
.
第1页(共14
页)
