2020-2021学年苏科新版八年级数学上册《第3章 勾股定理》单元测试卷(word解析版)
文档属性
| 名称 | 2020-2021学年苏科新版八年级数学上册《第3章 勾股定理》单元测试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-01 00:00:00 | ||
图片预览



文档简介
2020-2021学年苏科新版八年级数学上册《第3章
勾股定理》单元测试卷
一.选择题(共10小题)
1.在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则a4+b4的值为( )
A.35
B.43
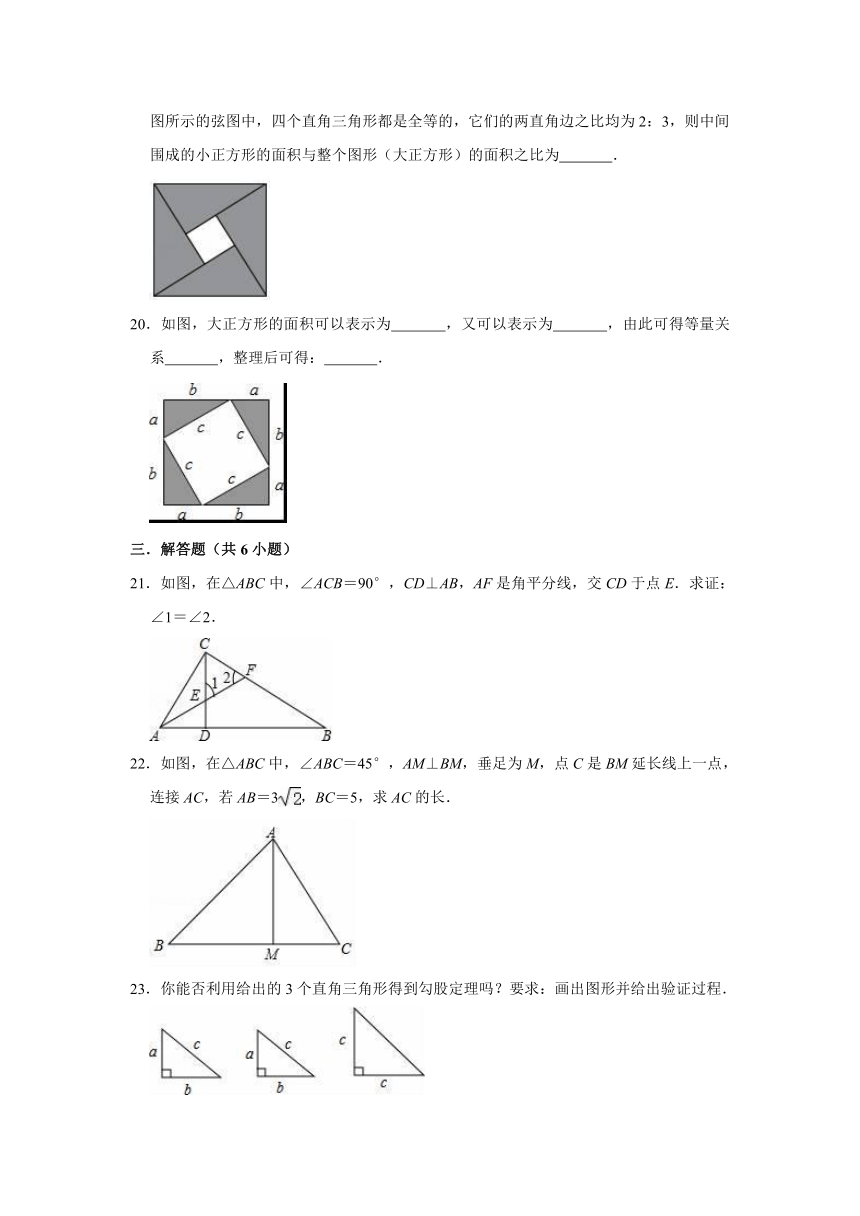
C.89
D.97
2.下列长度的3条线段能构成直角三角形的是( )
①8,15,17;②4,5,6;③7.5,4,8.5;④24,25,7;⑤5,8,17.
A.①②④
B.②④⑤
C.①③⑤
D.①③④
3.小丰妈妈买了一部29英寸(74cm)电视机,下列对29英寸的说法中正确的是( )
A.指的是屏幕的长度
B.指的是屏幕的宽度
C.指的是屏幕的周长
D.是屏幕对角线的长度
4.如图,已知直角△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA.∠ADE的度数为( )
A.56°
B.34°
C.44°
D.46°
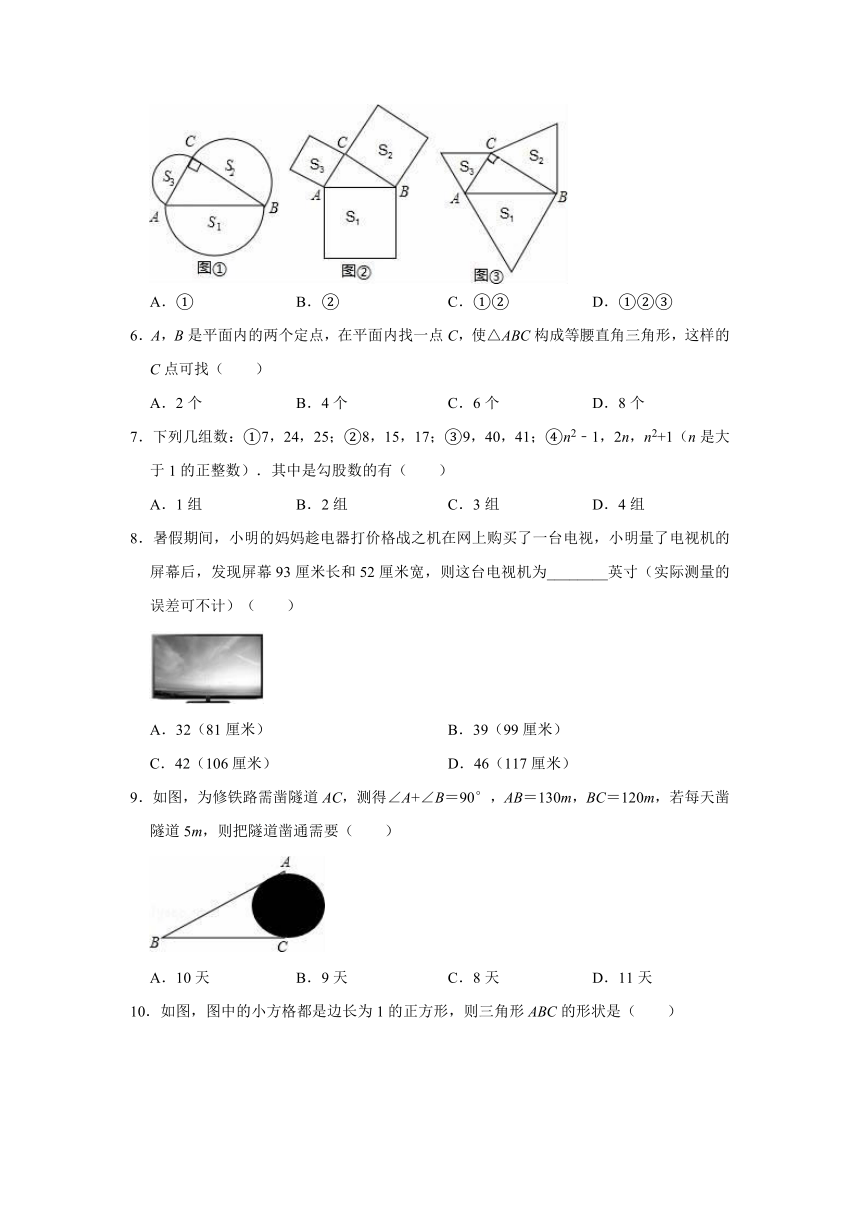
5.如图①,分别以Rt△ABC三边为直径向形外作三个半圆,其面积分别为S1,S2,S3;图②,分别以Rt△ABC三边为边向形外作三个正方形,其面积分别为S1,S2,S3;图③,分别以Rt△ABC三边为边向形外作三个等边三角形,其面积分别为S1,S2,S3.其中满足S1=S2+S3的有( )
A.①
B.②
C.①②
D.①②③
6.A,B是平面内的两个定点,在平面内找一点C,使△ABC构成等腰直角三角形,这样的C点可找( )
A.2个
B.4个
C.6个
D.8个
7.下列几组数:①7,24,25;②8,15,17;③9,40,41;④n2﹣1,2n,n2+1(n是大于1的正整数).其中是勾股数的有( )
A.1组
B.2组
C.3组
D.4组
8.暑假期间,小明的妈妈趁电器打价格战之机在网上购买了一台电视,小明量了电视机的屏幕后,发现屏幕93厘米长和52厘米宽,则这台电视机为________英寸(实际测量的误差可不计)( )
A.32(81厘米)
B.39(99厘米)
C.42(106厘米)
D.46(117厘米)
9.如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130m,BC=120m,若每天凿隧道5m,则把隧道凿通需要( )
A.10天
B.9天
C.8天
D.11天
10.如图,图中的小方格都是边长为1的正方形,则三角形ABC的形状是( )
A.钝角三角形
B.等腰直角三角形
C.锐角三角形
D.以上都有可能
二.填空题(共10小题)
11.在△ABC中,AC=17,AB=8,BC=15,则∠ABC=
.
12.如图,Rt△ABC中,直角边是
,斜边是
.
13.等腰直角三角形中,斜边上的高为acm,则这个三角形的面积为
.
14.在△ABC中,若a2=b2﹣c2,则△ABC是
三角形,
是直角;若a2<b2﹣c2,则∠B是
.
15.观察下列一组勾股数:①3,4,5;②5,12,13;③7,24,25;④9,40,41;⑤15,m,n.根据你发现的规律可得m+n=
.
16.如图所示,为测得池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长50m,BC长40m,则A,B两点间的距离是
m.
17.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1+∠2的度数为
.
18.若一个直角三角形的三边长分别是6、8、a,则a2=
.
19.汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2:3,则中间围成的小正方形的面积与整个图形(大正方形)的面积之比为
.
20.如图,大正方形的面积可以表示为
,又可以表示为
,由此可得等量关系
,整理后可得:
.
三.解答题(共6小题)
21.如图,在△ABC中,∠ACB=90°,CD⊥AB,AF是角平分线,交CD于点E.求证:∠1=∠2.
22.如图,在△ABC中,∠ABC=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC,若AB=3,BC=5,求AC的长.
23.你能否利用给出的3个直角三角形得到勾股定理吗?要求:画出图形并给出验证过程.
24.如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
①△ABC≌△DBE;②△ACB≌△ABD;
③△CBE≌△BED;④△ACE≌△ADE.
这些三角形真的全等吗?简要说明理由.
25.如图,∠C=90°,AC=12,BC=9,AD=8,BD=17,求△ABD的面积.
26.小明和小亮在同一所学校上学,放学后,小明先向东走1800米,再向南走200米到家,小亮先向北1000米,再向东走200米到家,根据题意,先画出示意图,再计算小明家和小亮家的距离.
参考答案与试题解析
一.选择题(共10小题)
1.解:依题意有:
a2+b2=大正方形的面积=13,
2ab=四个直角三角形的面积和=13﹣1=12,
ab=6,
则a4+b4
=(a2+b2)2﹣2a2b2
=(a2+b2)2﹣2(ab)2
=132﹣2×62
=169﹣72
=97.
故选:D.
2.解:①152+82=172,故能构成直角三角形;
②42+52≠62,故不能构成直角三角形;
③7.52+42=8.52,故能构成直角三角形;
④242+72=252,故能构成直角三角形;
⑤52+82≠172,故不能构成直角三角形;
故选:D.
3.解:29英寸指的是荧屏对角线的长度.
故选:D.
4.解:∵∠BAC=90°,DE∥AC(已知)
∴∠DEA=180°﹣∠BAC=90°(两直线平行,同旁内角互补).
∵AD⊥BC,∠B=56°,
∴∠BAD=34°,
在△ADE中,∵DE⊥AB,
∴∠ADE=56°.
故选:A.
5.解:∵S3=AC2,S2=BC2,S1=AB2,
∴S2+S3=S1.
由三个四边形都是正方形则:
∵S3=AC2,S2=BC2,S1=AB2,
∵三角形ABC是直角三角形,
又∵AC2+BC2=AB2,
∴S2+S3=S1.
∵S1=AB2,S2=BC2,S3=AC2,
∴S2+S3=S1.
故选:D.
6.解:A,B是平面内的两个定点,在平面内找一点C,使△ABC构成等腰直角三角形,
如图所示:
则这样的C点有6个,
故选:C.
7.解:①72+242=252,是勾股数;
②82+152=172,是勾股数;
③92+402=412,是勾股数;
④(n2﹣1)2+2n2=(n2﹣1)2,是勾股数.
故选:D.
8.解:根据勾股定理≈106.
故选:C.
9.解:∵∠A+∠B=90°,AB=130m,BC=120m,
∴AC===50(m).
∵每天凿隧道5m,
∴=10(天).
故选:A.
10.解:在直角△ABF、直角△BCD、直角△ACE中,
根据勾股定理即可得到:AB==;
BC=AC==,
则AB2=BC2+AC2,
故△ABC是等腰直角三角形.
故选:B.
二.填空题(共10小题)
11.解:∵△ABC中,AC=17,AB=8,BC=15,
∵152+82=172,即BC2+AB2=AC2,
∴∠ABC=90°.
故答案为90°.
12.解:Rt△ABC中,直角边是AC、BC,斜边是AB.
故答案为:AC、BC;AB.
13.解:∵等腰直角三角形中,斜边上的高为acm,
∴斜边=2acm,
∴S=×2a?a=a2(cm2).
答:这个等腰直角三角形的面积是a2cm2.
故答案为:a2cm2.
14.解:∵a2=b2﹣c2,
∴a2+c2=b2,
∴这个三角形是直角三角形,b是最长边,
∴b边所对的∠B为直角.
故答案为:直角;∠B;
在△ABC中,
∵a2<b2﹣c2,
∴a2+c2<b2,
由余弦定理可得:cosB=<0,
∴∠B为钝角,
故答案为:钝角.
15.解:由题意得:第n组数为(2n+1),,,
∴第1个数为15时,即相当于第7组数据,
∴m==112,
n==113,
m+n=112+113=225,
故答案为:225.
16.解:由题意得,AC=50m,BC=40m,∠ABC=90°,
∴在Rt△ABC中,AB===30(m).
故答案为:30.
17.解:由题意得:∠A=30°,∠ABC=∠ABD=90°,∠D=45°,
∴∠2=90°+45°=135°,
∴∠AEF=180°﹣∠2=45°,
∴∠1=∠A+AEF=30°+45°=75°,
∴∠1+∠2=135°+75°=210°;
故答案为:210°.
18.解:(1)若8是直角边,则第三边x是斜边,由勾股定理得:
62+82=a2,所以a2=100;
(2)若8是斜边,则第三边a为直角边,由勾股定理得:
62+x2=82,所以a2=28.
故答案为:100或28.
19.解:设两直角边分别是2x,3x,则斜边即大正方形的边长为x,小正方形边长为x,
所以S大正方形=13x2,S小正方形=x2,S阴影=12x2,
∴中间围成的小正方形的面积与整个图形(大正方形)的面积之比为=1:13;
故答案为:1:13.
20.解:大正方形的面积=(a+b)2,大正方形的面积=2ab+c2,则(a+b)2=2ab+c2,
∴a2+2ab+b2=2ab+c2.
∴a2+b2=c2.
故答案为:(a+b)2;2ab+c2;(a+b)2=2ab+c2;a2+b2=c2.
三.解答题(共6小题)
21.证明:∵AF是角平分线,
∴∠CAF=∠BAF,
∵∠ACB=90°,CD⊥AB,
∴∠CAF+∠2=90°,∠BAF+∠AED=90°,
∴∠2=∠AED,
∵∠1=∠AED,
∴∠1=∠2.
22.解:∵∠ABM=45°,AM⊥BM,
∴AM=BM.
∵AM2+BM2=AB2,AB=3,
∴AM=BM=3.
∴CM=BC﹣BM=5﹣3=2,
∴AC===.
23.解:如图,梯形的面积=(a+b)(a+b)=ab+ab+c2,
整理得,a2+b2=c2.
24.解:①△ABC≌△DBE,BC=BE,∠ABC=∠DBE=90°,AB=BD,符合SAS;
②△ACB与△ABD不全等,因为它们的形状不相同,
△ACB只是直角三角形,△ABD是等腰直角三角形;
③△CBE与△BED不全等,理由同②;
④△ACE与△ADE不全等,它们只有一边一角对应相等.
25.解:∵∠C=90°,AC=12,BC=9,
∴AB2=AC2+CB2,
∴AB=15.
∵AD=8,BD=17,
∴DB2=AD2+AB2,
∴∠DAB=90°,
∴△ABD的面积=AB×AD=60.
答:△ABD的面积为60.
26.解:如图所示:AB⊥BC,
由题意可得:AB=1200m,BC=1600m,
故AC==2000(m).
答:小明家和小亮家的距离为2000m.
勾股定理》单元测试卷
一.选择题(共10小题)
1.在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则a4+b4的值为( )
A.35
B.43
C.89
D.97
2.下列长度的3条线段能构成直角三角形的是( )
①8,15,17;②4,5,6;③7.5,4,8.5;④24,25,7;⑤5,8,17.
A.①②④
B.②④⑤
C.①③⑤
D.①③④
3.小丰妈妈买了一部29英寸(74cm)电视机,下列对29英寸的说法中正确的是( )
A.指的是屏幕的长度
B.指的是屏幕的宽度
C.指的是屏幕的周长
D.是屏幕对角线的长度
4.如图,已知直角△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA.∠ADE的度数为( )
A.56°
B.34°
C.44°
D.46°
5.如图①,分别以Rt△ABC三边为直径向形外作三个半圆,其面积分别为S1,S2,S3;图②,分别以Rt△ABC三边为边向形外作三个正方形,其面积分别为S1,S2,S3;图③,分别以Rt△ABC三边为边向形外作三个等边三角形,其面积分别为S1,S2,S3.其中满足S1=S2+S3的有( )
A.①
B.②
C.①②
D.①②③
6.A,B是平面内的两个定点,在平面内找一点C,使△ABC构成等腰直角三角形,这样的C点可找( )
A.2个
B.4个
C.6个
D.8个
7.下列几组数:①7,24,25;②8,15,17;③9,40,41;④n2﹣1,2n,n2+1(n是大于1的正整数).其中是勾股数的有( )
A.1组
B.2组
C.3组
D.4组
8.暑假期间,小明的妈妈趁电器打价格战之机在网上购买了一台电视,小明量了电视机的屏幕后,发现屏幕93厘米长和52厘米宽,则这台电视机为________英寸(实际测量的误差可不计)( )
A.32(81厘米)
B.39(99厘米)
C.42(106厘米)
D.46(117厘米)
9.如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130m,BC=120m,若每天凿隧道5m,则把隧道凿通需要( )
A.10天
B.9天
C.8天
D.11天
10.如图,图中的小方格都是边长为1的正方形,则三角形ABC的形状是( )
A.钝角三角形
B.等腰直角三角形
C.锐角三角形
D.以上都有可能
二.填空题(共10小题)
11.在△ABC中,AC=17,AB=8,BC=15,则∠ABC=
.
12.如图,Rt△ABC中,直角边是
,斜边是
.
13.等腰直角三角形中,斜边上的高为acm,则这个三角形的面积为
.
14.在△ABC中,若a2=b2﹣c2,则△ABC是
三角形,
是直角;若a2<b2﹣c2,则∠B是
.
15.观察下列一组勾股数:①3,4,5;②5,12,13;③7,24,25;④9,40,41;⑤15,m,n.根据你发现的规律可得m+n=
.
16.如图所示,为测得池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长50m,BC长40m,则A,B两点间的距离是
m.
17.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1+∠2的度数为
.
18.若一个直角三角形的三边长分别是6、8、a,则a2=
.
19.汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2:3,则中间围成的小正方形的面积与整个图形(大正方形)的面积之比为
.
20.如图,大正方形的面积可以表示为
,又可以表示为
,由此可得等量关系
,整理后可得:
.
三.解答题(共6小题)
21.如图,在△ABC中,∠ACB=90°,CD⊥AB,AF是角平分线,交CD于点E.求证:∠1=∠2.
22.如图,在△ABC中,∠ABC=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC,若AB=3,BC=5,求AC的长.
23.你能否利用给出的3个直角三角形得到勾股定理吗?要求:画出图形并给出验证过程.
24.如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
①△ABC≌△DBE;②△ACB≌△ABD;
③△CBE≌△BED;④△ACE≌△ADE.
这些三角形真的全等吗?简要说明理由.
25.如图,∠C=90°,AC=12,BC=9,AD=8,BD=17,求△ABD的面积.
26.小明和小亮在同一所学校上学,放学后,小明先向东走1800米,再向南走200米到家,小亮先向北1000米,再向东走200米到家,根据题意,先画出示意图,再计算小明家和小亮家的距离.
参考答案与试题解析
一.选择题(共10小题)
1.解:依题意有:
a2+b2=大正方形的面积=13,
2ab=四个直角三角形的面积和=13﹣1=12,
ab=6,
则a4+b4
=(a2+b2)2﹣2a2b2
=(a2+b2)2﹣2(ab)2
=132﹣2×62
=169﹣72
=97.
故选:D.
2.解:①152+82=172,故能构成直角三角形;
②42+52≠62,故不能构成直角三角形;
③7.52+42=8.52,故能构成直角三角形;
④242+72=252,故能构成直角三角形;
⑤52+82≠172,故不能构成直角三角形;
故选:D.
3.解:29英寸指的是荧屏对角线的长度.
故选:D.
4.解:∵∠BAC=90°,DE∥AC(已知)
∴∠DEA=180°﹣∠BAC=90°(两直线平行,同旁内角互补).
∵AD⊥BC,∠B=56°,
∴∠BAD=34°,
在△ADE中,∵DE⊥AB,
∴∠ADE=56°.
故选:A.
5.解:∵S3=AC2,S2=BC2,S1=AB2,
∴S2+S3=S1.
由三个四边形都是正方形则:
∵S3=AC2,S2=BC2,S1=AB2,
∵三角形ABC是直角三角形,
又∵AC2+BC2=AB2,
∴S2+S3=S1.
∵S1=AB2,S2=BC2,S3=AC2,
∴S2+S3=S1.
故选:D.
6.解:A,B是平面内的两个定点,在平面内找一点C,使△ABC构成等腰直角三角形,
如图所示:
则这样的C点有6个,
故选:C.
7.解:①72+242=252,是勾股数;
②82+152=172,是勾股数;
③92+402=412,是勾股数;
④(n2﹣1)2+2n2=(n2﹣1)2,是勾股数.
故选:D.
8.解:根据勾股定理≈106.
故选:C.
9.解:∵∠A+∠B=90°,AB=130m,BC=120m,
∴AC===50(m).
∵每天凿隧道5m,
∴=10(天).
故选:A.
10.解:在直角△ABF、直角△BCD、直角△ACE中,
根据勾股定理即可得到:AB==;
BC=AC==,
则AB2=BC2+AC2,
故△ABC是等腰直角三角形.
故选:B.
二.填空题(共10小题)
11.解:∵△ABC中,AC=17,AB=8,BC=15,
∵152+82=172,即BC2+AB2=AC2,
∴∠ABC=90°.
故答案为90°.
12.解:Rt△ABC中,直角边是AC、BC,斜边是AB.
故答案为:AC、BC;AB.
13.解:∵等腰直角三角形中,斜边上的高为acm,
∴斜边=2acm,
∴S=×2a?a=a2(cm2).
答:这个等腰直角三角形的面积是a2cm2.
故答案为:a2cm2.
14.解:∵a2=b2﹣c2,
∴a2+c2=b2,
∴这个三角形是直角三角形,b是最长边,
∴b边所对的∠B为直角.
故答案为:直角;∠B;
在△ABC中,
∵a2<b2﹣c2,
∴a2+c2<b2,
由余弦定理可得:cosB=<0,
∴∠B为钝角,
故答案为:钝角.
15.解:由题意得:第n组数为(2n+1),,,
∴第1个数为15时,即相当于第7组数据,
∴m==112,
n==113,
m+n=112+113=225,
故答案为:225.
16.解:由题意得,AC=50m,BC=40m,∠ABC=90°,
∴在Rt△ABC中,AB===30(m).
故答案为:30.
17.解:由题意得:∠A=30°,∠ABC=∠ABD=90°,∠D=45°,
∴∠2=90°+45°=135°,
∴∠AEF=180°﹣∠2=45°,
∴∠1=∠A+AEF=30°+45°=75°,
∴∠1+∠2=135°+75°=210°;
故答案为:210°.
18.解:(1)若8是直角边,则第三边x是斜边,由勾股定理得:
62+82=a2,所以a2=100;
(2)若8是斜边,则第三边a为直角边,由勾股定理得:
62+x2=82,所以a2=28.
故答案为:100或28.
19.解:设两直角边分别是2x,3x,则斜边即大正方形的边长为x,小正方形边长为x,
所以S大正方形=13x2,S小正方形=x2,S阴影=12x2,
∴中间围成的小正方形的面积与整个图形(大正方形)的面积之比为=1:13;
故答案为:1:13.
20.解:大正方形的面积=(a+b)2,大正方形的面积=2ab+c2,则(a+b)2=2ab+c2,
∴a2+2ab+b2=2ab+c2.
∴a2+b2=c2.
故答案为:(a+b)2;2ab+c2;(a+b)2=2ab+c2;a2+b2=c2.
三.解答题(共6小题)
21.证明:∵AF是角平分线,
∴∠CAF=∠BAF,
∵∠ACB=90°,CD⊥AB,
∴∠CAF+∠2=90°,∠BAF+∠AED=90°,
∴∠2=∠AED,
∵∠1=∠AED,
∴∠1=∠2.
22.解:∵∠ABM=45°,AM⊥BM,
∴AM=BM.
∵AM2+BM2=AB2,AB=3,
∴AM=BM=3.
∴CM=BC﹣BM=5﹣3=2,
∴AC===.
23.解:如图,梯形的面积=(a+b)(a+b)=ab+ab+c2,
整理得,a2+b2=c2.
24.解:①△ABC≌△DBE,BC=BE,∠ABC=∠DBE=90°,AB=BD,符合SAS;
②△ACB与△ABD不全等,因为它们的形状不相同,
△ACB只是直角三角形,△ABD是等腰直角三角形;
③△CBE与△BED不全等,理由同②;
④△ACE与△ADE不全等,它们只有一边一角对应相等.
25.解:∵∠C=90°,AC=12,BC=9,
∴AB2=AC2+CB2,
∴AB=15.
∵AD=8,BD=17,
∴DB2=AD2+AB2,
∴∠DAB=90°,
∴△ABD的面积=AB×AD=60.
答:△ABD的面积为60.
26.解:如图所示:AB⊥BC,
由题意可得:AB=1200m,BC=1600m,
故AC==2000(m).
答:小明家和小亮家的距离为2000m.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
