2020-2021学年苏科新版八年级数学上册《第6章 一次函数》单元测试卷(word解析版)
文档属性
| 名称 | 2020-2021学年苏科新版八年级数学上册《第6章 一次函数》单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 245.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-01 21:57:54 | ||
图片预览



文档简介
2020-2021学年苏科新版八年级数学上册《第6章
一次函数》单元测试卷
一.选择题(共10小题)
1.我们都知道,圆的周长计算公式是c=2πr,下列说法正确的是( )
A.c,π,r都是变量
B.只有r是变量
C.只有c是变量
D.c,r是变量
2.在等式①x=|y|;②y=|x|;③x2+y2﹣1=0;④5x﹣2y=0;⑤,y是x的函数的有( )
A.2个
B.3个
C.4个
D.5个
3.在函数y=+中,自变量x的取值范围是( )
A.x≥2
B.x≤2
C.2≤x≤3
D.x≤2或x≥3
4.下列函数中,是一次函数的有( )
①;②y=4x;③;④;⑤y=2x2﹣1.
A.1个
B.2个
C.3个
D.4个
5.下列关系式中,表示y是x的正比例函数的是( )
A.y=
B.y=1
C.y=x+1
D.y=2x
6.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的( )
A.
B.
C.
D.
7.邮购一种图书,每册定价20元,另加书价的5%作邮资,购书x册,需付款y(元)与x的函数解析式为( )
A.y=20x+5%x
B.y=20.05x
C.y=20(1+5%)x
D.y=19.95x
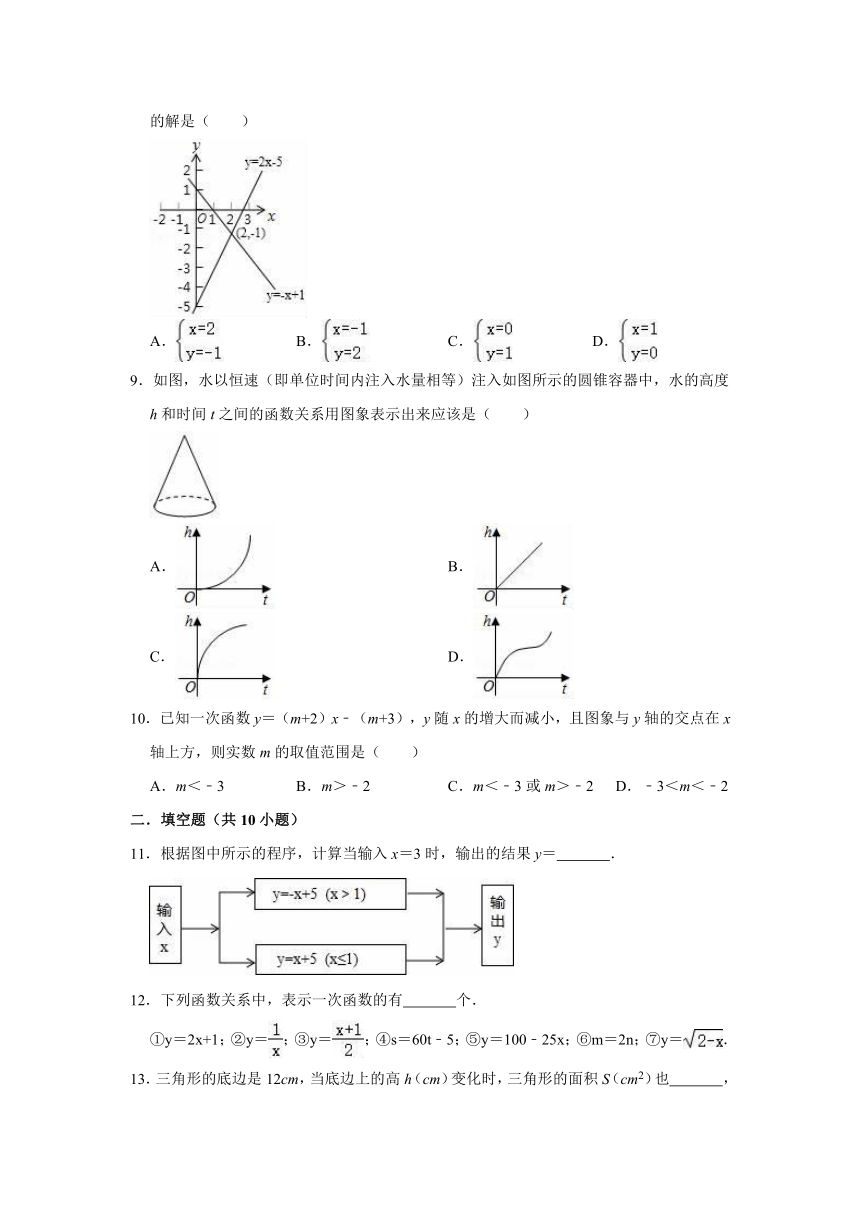
8.如图所示,在直角坐标系中的两条直线分别是y=﹣x+1和y=2x﹣5,那么方程组的解是( )
A.
B.
C.
D.
9.如图,水以恒速(即单位时间内注入水量相等)注入如图所示的圆锥容器中,水的高度h和时间t之间的函数关系用图象表示出来应该是( )
A.
B.
C.
D.
10.已知一次函数y=(m+2)x﹣(m+3),y随x的增大而减小,且图象与y轴的交点在x轴上方,则实数m的取值范围是( )
A.m<﹣3
B.m>﹣2
C.m<﹣3或m>﹣2
D.﹣3<m<﹣2
二.填空题(共10小题)
11.根据图中所示的程序,计算当输入x=3时,输出的结果y=
.
12.下列函数关系中,表示一次函数的有
个.
①y=2x+1;②y=;③y=;④s=60t﹣5;⑤y=100﹣25x;⑥m=2n;⑦y=.
13.三角形的底边是12cm,当底边上的高h(cm)变化时,三角形的面积S(cm2)也
,其中
是自变量,
是因变量,可用式子表示成S=
.
14.拖拉机耕地,油箱内装有油42升,如果每小时耗油5升,写出所剩油量w(升)与时间t(小时)之间的函数关系式
,其中
是常量,
是变量.
15.观察下表:则y与x的关系式为
.
x
1
2
3
4
5
…
y
2
9
28
65
126
…
16.根据一次函数y=﹣3x﹣6的图象,当函数值大于零时,x的范围是
.
17.一个矩形的周长为6,一条边长为x,另一条边长为y,则用x表示y的函数表达式为
(0<x<3)
18.若一次函数y=3x﹣7与y=2x+8的交点P的坐标为(15,38),则方程组的解为
.
19.一元一次方程0.5x+1=0的解是一次函数y=0.5x+1的图象与
的横坐标.
20.如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是
,直线AE的解析式是
.
三.解答题(共7小题)
21.一个圆柱的高等于底面半径,写出它的表面积S与底面半径r之间的关系式.
22.已知关于x的函数y=(m+1)x+(m2﹣1).
(1)当m取什么值时,y是x的一次函数?
(2)当m取什么值时,y是x的正比例函数?
(3)当m取什么值时,该函数与函数y=﹣x+3是同一个函数?
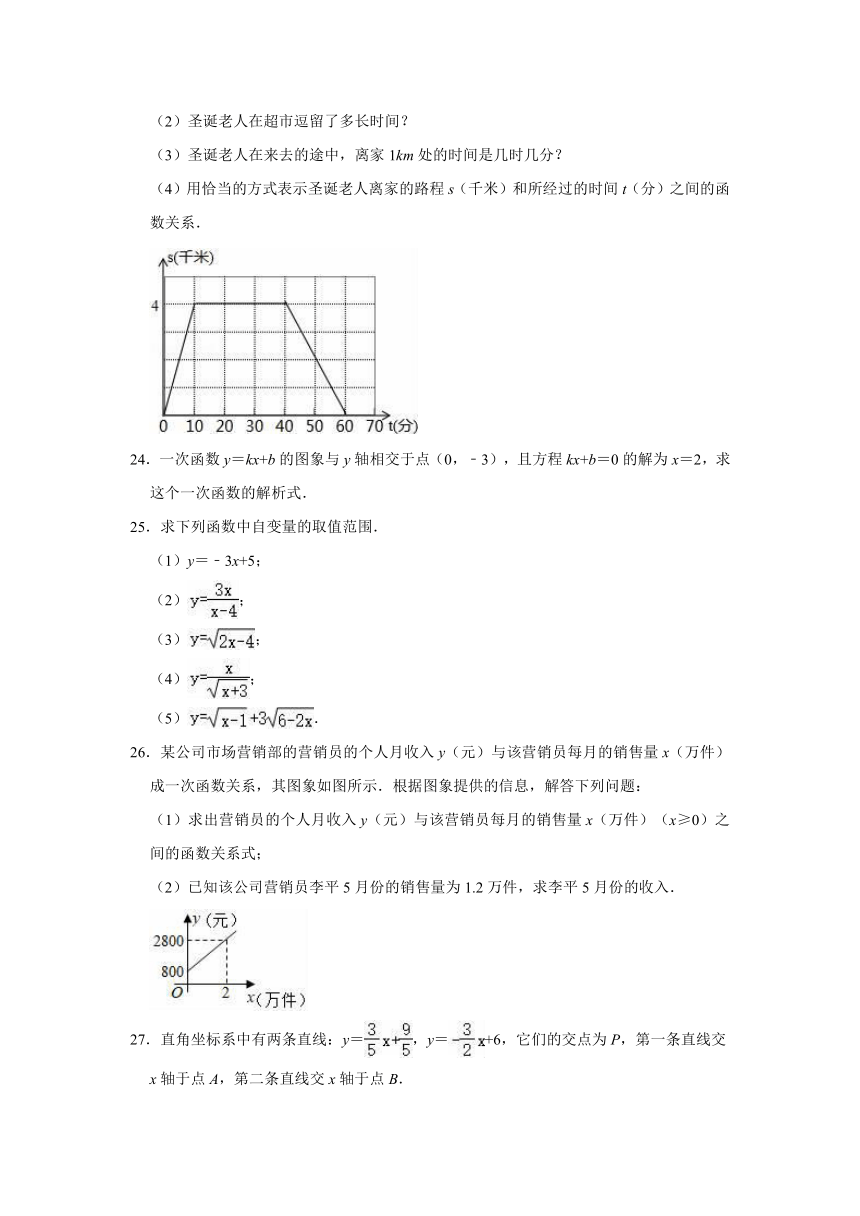
23.圣诞老人上午8:00从家里出发,骑车去一家超市购物,然后从这家超市回到家中,圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,
请根据图象回到问题:
(1)圣诞老人去超市途中的速度是多少?回家途中的速度是多少?
(2)圣诞老人在超市逗留了多长时间?
(3)圣诞老人在来去的途中,离家1km处的时间是几时几分?
(4)用恰当的方式表示圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系.
24.一次函数y=kx+b的图象与y轴相交于点(0,﹣3),且方程kx+b=0的解为x=2,求这个一次函数的解析式.
25.求下列函数中自变量的取值范围.
(1)y=﹣3x+5;
(2);
(3);
(4);
(5).
26.某公司市场营销部的营销员的个人月收入y(元)与该营销员每月的销售量x(万件)成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
(1)求出营销员的个人月收入y(元)与该营销员每月的销售量x(万件)(x≥0)之间的函数关系式;
(2)已知该公司营销员李平5月份的销售量为1.2万件,求李平5月份的收入.
27.直角坐标系中有两条直线:y=,y=+6,它们的交点为P,第一条直线交x轴于点A,第二条直线交x轴于点B.
(1)求A、B两点坐标;
(2)用图象法解方程组
(3)求△PAB的面积.
参考答案与试题解析
一.选择题(共10小题)
1.解:圆的周长计算公式是c=2πr,C和r是变量,2、π是常量,
故选:D.
2.解:∵对于x的每一个取值,y都有唯一确定的值,
∴②y=|x|;④5x﹣2y=0;⑤当x取值时,y有唯一的值对应;
故选:B.
3.解:由题意得,x﹣2≥0且3﹣x≥0,
解得x≥2且x≤3,
所以,2≤x≤3.
故选:C.
4.解:①y=是反比例函数,故本选项错误;
②y=4x是一次函数,故本选项正确;
③y=x是一次函数,故本选项正确;
④y=﹣+1是一次函数,故本选项正确;
⑤y=2x2﹣1是二次函数,故本选项错误.
故正确的有3个.
故选:C.
5.解:A、是反比例函数,故A错误;
B、是常函数,故B错误;
C、是一次函数,故C错误;
D、是正比例函数,故正确;
故选:D.
6.解:整理为y=kx﹣2
∵y随x的增大而减小
∴k<0
又因为图象过2,4,3象限
故选:D.
7.解:由题意得;购买一册书需要花费(20+20×5%)元
∴购买x册数需花费x(20+20×5%)元
即:y=x(20+20×5%)=20(1+5%)x
故选:C.
8.解:由图可知,直线y=﹣x+1和y=2x﹣5的交点坐标为(2,﹣1);
因此方程组的解是.
故选:A.
9.解:∵容器下底大而上口小,
∴将水以恒速注入,
则容器内对应的水高度h随时间t的增加而增加,但增加的速度越来越快,
∴h与t的函数图象只可能是A,
故选:A.
10.解:由题意得:
解得:m<﹣3
故选:A.
二.填空题(共10小题)
11.解:由图可知,x=3时,y=﹣3+5=2.
故答案为:2.
12.一次函数有y=2x+1,y=,s=60t﹣5,y=100﹣25x,m=2n,共5个,
故答案为:5.
13.解:三角形的面积S(cm2)也
变化,其中
h是自变量,S是因变量,可用式子表示成S=6h,
故答案为:变化,h,S,6h.
14.解:由题意可得出:
w=42﹣5t,其中42,5是常量,w,t是变量.
故答案为:w=42﹣5t,42,5,w,t.
15.解:当x=1时,y=13+1=2;
当x=2时,y=22+1=9;
当x=3时,y=33+1=28;
…
由此可得出y=x3+1.
16.解:由函数y=﹣3x﹣6可知,此函数与两坐标轴的交点分别为(0,﹣6)、(﹣2,0),
由函数图象可知,当函数值大于零时,x的范围是x<﹣2.
17.解:由题意得,2(x+y)=6,
故:y=3﹣x(0<x<3).
故答案为:y=3﹣x.
18.解:一次函数y=3x﹣7与y=2x+8的交点P的坐标为(15,38),
所以x=15,y=38同时满足两个函数解析式,
则是二元一次方程组的解.
故答案为.
19.解:∵0.5x+1=0,∴0.5x=﹣1,
∴x=﹣2,
∴一次函数y=0.5x+1的图象与x轴交点的横坐标为:x=﹣2,
故答案为:x轴交点.
20.解:由于正方形ABCO的边长是2,E是BC中点,
则A(0,2),E(2,1);
设直线AE的解析式为y=kx+b,
则,解得:;
故直线AE的解析式是y=﹣x+2.
三.解答题(共7小题)
21.解:由圆柱的表面积=2×圆柱的底面积+圆柱的侧面积,得
S=2πr2+2πr?r=4πr2.
22.解:(1)根据一次函数的定义可知:m+1≠0,
解得:m≠﹣1.
(2)∵函数y=(m+1)x+(m2﹣1)是正比例函数,
∴m+1≠0且m2﹣1=0.
解得:m=1.
(3)∵该函数与函数y=﹣x+3是同一个函数,
∴m+1=﹣1且m2﹣1=3.
解得:m=﹣2.
23.解:(1)由横坐标看出,去超市用了10分钟,从超市返回用了20分钟,由纵坐标看出,家到超市的距离是4千米,
去超市的速度是4÷10=(千米/分钟);从超市返回的速度是4÷20=(千米/分钟);
(2)由横坐标看出,在超市逗留的时间40﹣10=30(分钟);
(3)去超市时1÷=(分钟),返回时3÷=15,40+15=55(分钟);
(4)用恰当的方式表示圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系
s=.
24.解:∵方程kx+b=0的解为x=2,
∴一次函数y=kx+b的图象经过点(2,0).
把(0,﹣3)、(2,0)代入y=kx+b中,
得,
解得.
故一次函数的解析式是y=x﹣3.
25.解:(1)x的取值范围为全体实数;
(2)解不等式x﹣4≠0,得x≠4,故x的取值范围为x≠4;
(3)解不等式2x﹣4≥0,得x≥2,故x的取值范围为x≥2;
(4)解不等式x+3>0,得x>﹣3,故x的取值范围为x>﹣3;
(5)解不等式组得1≤x≤3,故x的取值范围为1≤x≤3.
26.解:(1)设所求的函数关系式为y=kx+b,
∵函数图象过(0,800)和(2,2800)两点,
∴,
解得,,
即营销员的个人月收入y(元)与该营销员每月的销售量x(万件)(x≥0)之间的函数关系式为y=1000x+800(x≥0);
(2)当x=1.2时,y=1000×1.2+800=2000,
即李平5月份的收入为2000元.
27.解:(1)令y=0,则=0,
解得x=﹣3,
所以点A的坐标为(﹣3,0),
令+6=0,
解得x=4,
所以,点B的坐标为(4,0);
(2)如图所示,方程组的解是;
(3)AB=4﹣(﹣3)=4+3=7,
△PAB的面积=×7×3=.
一次函数》单元测试卷
一.选择题(共10小题)
1.我们都知道,圆的周长计算公式是c=2πr,下列说法正确的是( )
A.c,π,r都是变量
B.只有r是变量
C.只有c是变量
D.c,r是变量
2.在等式①x=|y|;②y=|x|;③x2+y2﹣1=0;④5x﹣2y=0;⑤,y是x的函数的有( )
A.2个
B.3个
C.4个
D.5个
3.在函数y=+中,自变量x的取值范围是( )
A.x≥2
B.x≤2
C.2≤x≤3
D.x≤2或x≥3
4.下列函数中,是一次函数的有( )
①;②y=4x;③;④;⑤y=2x2﹣1.
A.1个
B.2个
C.3个
D.4个
5.下列关系式中,表示y是x的正比例函数的是( )
A.y=
B.y=1
C.y=x+1
D.y=2x
6.函数kx﹣y=2中,y随x的增大而减小,则它的图象是下图中的( )
A.
B.
C.
D.
7.邮购一种图书,每册定价20元,另加书价的5%作邮资,购书x册,需付款y(元)与x的函数解析式为( )
A.y=20x+5%x
B.y=20.05x
C.y=20(1+5%)x
D.y=19.95x
8.如图所示,在直角坐标系中的两条直线分别是y=﹣x+1和y=2x﹣5,那么方程组的解是( )
A.
B.
C.
D.
9.如图,水以恒速(即单位时间内注入水量相等)注入如图所示的圆锥容器中,水的高度h和时间t之间的函数关系用图象表示出来应该是( )
A.
B.
C.
D.
10.已知一次函数y=(m+2)x﹣(m+3),y随x的增大而减小,且图象与y轴的交点在x轴上方,则实数m的取值范围是( )
A.m<﹣3
B.m>﹣2
C.m<﹣3或m>﹣2
D.﹣3<m<﹣2
二.填空题(共10小题)
11.根据图中所示的程序,计算当输入x=3时,输出的结果y=
.
12.下列函数关系中,表示一次函数的有
个.
①y=2x+1;②y=;③y=;④s=60t﹣5;⑤y=100﹣25x;⑥m=2n;⑦y=.
13.三角形的底边是12cm,当底边上的高h(cm)变化时,三角形的面积S(cm2)也
,其中
是自变量,
是因变量,可用式子表示成S=
.
14.拖拉机耕地,油箱内装有油42升,如果每小时耗油5升,写出所剩油量w(升)与时间t(小时)之间的函数关系式
,其中
是常量,
是变量.
15.观察下表:则y与x的关系式为
.
x
1
2
3
4
5
…
y
2
9
28
65
126
…
16.根据一次函数y=﹣3x﹣6的图象,当函数值大于零时,x的范围是
.
17.一个矩形的周长为6,一条边长为x,另一条边长为y,则用x表示y的函数表达式为
(0<x<3)
18.若一次函数y=3x﹣7与y=2x+8的交点P的坐标为(15,38),则方程组的解为
.
19.一元一次方程0.5x+1=0的解是一次函数y=0.5x+1的图象与
的横坐标.
20.如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是
,直线AE的解析式是
.
三.解答题(共7小题)
21.一个圆柱的高等于底面半径,写出它的表面积S与底面半径r之间的关系式.
22.已知关于x的函数y=(m+1)x+(m2﹣1).
(1)当m取什么值时,y是x的一次函数?
(2)当m取什么值时,y是x的正比例函数?
(3)当m取什么值时,该函数与函数y=﹣x+3是同一个函数?
23.圣诞老人上午8:00从家里出发,骑车去一家超市购物,然后从这家超市回到家中,圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,
请根据图象回到问题:
(1)圣诞老人去超市途中的速度是多少?回家途中的速度是多少?
(2)圣诞老人在超市逗留了多长时间?
(3)圣诞老人在来去的途中,离家1km处的时间是几时几分?
(4)用恰当的方式表示圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系.
24.一次函数y=kx+b的图象与y轴相交于点(0,﹣3),且方程kx+b=0的解为x=2,求这个一次函数的解析式.
25.求下列函数中自变量的取值范围.
(1)y=﹣3x+5;
(2);
(3);
(4);
(5).
26.某公司市场营销部的营销员的个人月收入y(元)与该营销员每月的销售量x(万件)成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
(1)求出营销员的个人月收入y(元)与该营销员每月的销售量x(万件)(x≥0)之间的函数关系式;
(2)已知该公司营销员李平5月份的销售量为1.2万件,求李平5月份的收入.
27.直角坐标系中有两条直线:y=,y=+6,它们的交点为P,第一条直线交x轴于点A,第二条直线交x轴于点B.
(1)求A、B两点坐标;
(2)用图象法解方程组
(3)求△PAB的面积.
参考答案与试题解析
一.选择题(共10小题)
1.解:圆的周长计算公式是c=2πr,C和r是变量,2、π是常量,
故选:D.
2.解:∵对于x的每一个取值,y都有唯一确定的值,
∴②y=|x|;④5x﹣2y=0;⑤当x取值时,y有唯一的值对应;
故选:B.
3.解:由题意得,x﹣2≥0且3﹣x≥0,
解得x≥2且x≤3,
所以,2≤x≤3.
故选:C.
4.解:①y=是反比例函数,故本选项错误;
②y=4x是一次函数,故本选项正确;
③y=x是一次函数,故本选项正确;
④y=﹣+1是一次函数,故本选项正确;
⑤y=2x2﹣1是二次函数,故本选项错误.
故正确的有3个.
故选:C.
5.解:A、是反比例函数,故A错误;
B、是常函数,故B错误;
C、是一次函数,故C错误;
D、是正比例函数,故正确;
故选:D.
6.解:整理为y=kx﹣2
∵y随x的增大而减小
∴k<0
又因为图象过2,4,3象限
故选:D.
7.解:由题意得;购买一册书需要花费(20+20×5%)元
∴购买x册数需花费x(20+20×5%)元
即:y=x(20+20×5%)=20(1+5%)x
故选:C.
8.解:由图可知,直线y=﹣x+1和y=2x﹣5的交点坐标为(2,﹣1);
因此方程组的解是.
故选:A.
9.解:∵容器下底大而上口小,
∴将水以恒速注入,
则容器内对应的水高度h随时间t的增加而增加,但增加的速度越来越快,
∴h与t的函数图象只可能是A,
故选:A.
10.解:由题意得:
解得:m<﹣3
故选:A.
二.填空题(共10小题)
11.解:由图可知,x=3时,y=﹣3+5=2.
故答案为:2.
12.一次函数有y=2x+1,y=,s=60t﹣5,y=100﹣25x,m=2n,共5个,
故答案为:5.
13.解:三角形的面积S(cm2)也
变化,其中
h是自变量,S是因变量,可用式子表示成S=6h,
故答案为:变化,h,S,6h.
14.解:由题意可得出:
w=42﹣5t,其中42,5是常量,w,t是变量.
故答案为:w=42﹣5t,42,5,w,t.
15.解:当x=1时,y=13+1=2;
当x=2时,y=22+1=9;
当x=3时,y=33+1=28;
…
由此可得出y=x3+1.
16.解:由函数y=﹣3x﹣6可知,此函数与两坐标轴的交点分别为(0,﹣6)、(﹣2,0),
由函数图象可知,当函数值大于零时,x的范围是x<﹣2.
17.解:由题意得,2(x+y)=6,
故:y=3﹣x(0<x<3).
故答案为:y=3﹣x.
18.解:一次函数y=3x﹣7与y=2x+8的交点P的坐标为(15,38),
所以x=15,y=38同时满足两个函数解析式,
则是二元一次方程组的解.
故答案为.
19.解:∵0.5x+1=0,∴0.5x=﹣1,
∴x=﹣2,
∴一次函数y=0.5x+1的图象与x轴交点的横坐标为:x=﹣2,
故答案为:x轴交点.
20.解:由于正方形ABCO的边长是2,E是BC中点,
则A(0,2),E(2,1);
设直线AE的解析式为y=kx+b,
则,解得:;
故直线AE的解析式是y=﹣x+2.
三.解答题(共7小题)
21.解:由圆柱的表面积=2×圆柱的底面积+圆柱的侧面积,得
S=2πr2+2πr?r=4πr2.
22.解:(1)根据一次函数的定义可知:m+1≠0,
解得:m≠﹣1.
(2)∵函数y=(m+1)x+(m2﹣1)是正比例函数,
∴m+1≠0且m2﹣1=0.
解得:m=1.
(3)∵该函数与函数y=﹣x+3是同一个函数,
∴m+1=﹣1且m2﹣1=3.
解得:m=﹣2.
23.解:(1)由横坐标看出,去超市用了10分钟,从超市返回用了20分钟,由纵坐标看出,家到超市的距离是4千米,
去超市的速度是4÷10=(千米/分钟);从超市返回的速度是4÷20=(千米/分钟);
(2)由横坐标看出,在超市逗留的时间40﹣10=30(分钟);
(3)去超市时1÷=(分钟),返回时3÷=15,40+15=55(分钟);
(4)用恰当的方式表示圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系
s=.
24.解:∵方程kx+b=0的解为x=2,
∴一次函数y=kx+b的图象经过点(2,0).
把(0,﹣3)、(2,0)代入y=kx+b中,
得,
解得.
故一次函数的解析式是y=x﹣3.
25.解:(1)x的取值范围为全体实数;
(2)解不等式x﹣4≠0,得x≠4,故x的取值范围为x≠4;
(3)解不等式2x﹣4≥0,得x≥2,故x的取值范围为x≥2;
(4)解不等式x+3>0,得x>﹣3,故x的取值范围为x>﹣3;
(5)解不等式组得1≤x≤3,故x的取值范围为1≤x≤3.
26.解:(1)设所求的函数关系式为y=kx+b,
∵函数图象过(0,800)和(2,2800)两点,
∴,
解得,,
即营销员的个人月收入y(元)与该营销员每月的销售量x(万件)(x≥0)之间的函数关系式为y=1000x+800(x≥0);
(2)当x=1.2时,y=1000×1.2+800=2000,
即李平5月份的收入为2000元.
27.解:(1)令y=0,则=0,
解得x=﹣3,
所以点A的坐标为(﹣3,0),
令+6=0,
解得x=4,
所以,点B的坐标为(4,0);
(2)如图所示,方程组的解是;
(3)AB=4﹣(﹣3)=4+3=7,
△PAB的面积=×7×3=.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
