人教版九年级上册数学 24.2.2直线与圆的位置关系 同步习题(Word版 含解析)
文档属性
| 名称 | 人教版九年级上册数学 24.2.2直线与圆的位置关系 同步习题(Word版 含解析) | 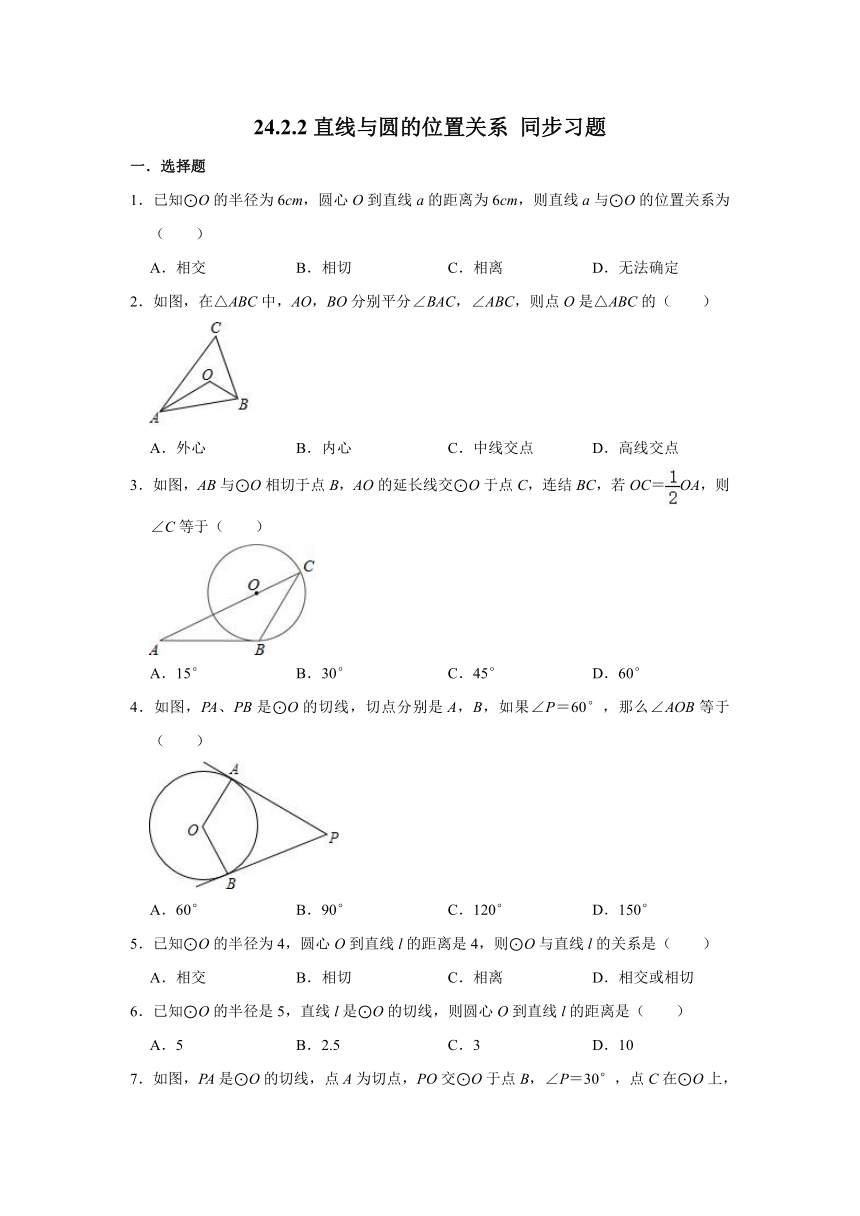 | |
| 格式 | zip | ||
| 文件大小 | 163.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-01 22:26:31 | ||
图片预览




文档简介
24.2.2直线与圆的位置关系
同步习题
一.选择题
1.已知⊙O的半径为6cm,圆心O到直线a的距离为6cm,则直线a与⊙O的位置关系为( )
A.相交
B.相切
C.相离
D.无法确定
2.如图,在△ABC中,AO,BO分别平分∠BAC,∠ABC,则点O是△ABC的( )
A.外心
B.内心
C.中线交点
D.高线交点
3.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC,若OC=OA,则∠C等于( )
A.15°
B.30°
C.45°
D.60°
4.如图,PA、PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
A.60°
B.90°
C.120°
D.150°
5.已知⊙O的半径为4,圆心O到直线l的距离是4,则⊙O与直线l的关系是( )
A.相交
B.相切
C.相离
D.相交或相切
6.已知⊙O的半径是5,直线l是⊙O的切线,则圆心O到直线l的距离是( )
A.5
B.2.5
C.3
D.10
7.如图,PA是⊙O的切线,点A为切点,PO交⊙O于点B,∠P=30°,点C在⊙O上,连接AC,BC,则∠ACB的度数为( )
A.25°
B.28°
C.30°
D.35°
8.如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=32°,则∠ACB的度数是( )
A.29°
B.30°
C.31°
D.32°
9.如图,在△ABC中,O是BC边上的点,以点O为圆心,BO为半径的⊙O与AC相切于点A,D是优弧AB上一点,∠ADB=65°,则∠C的度数是( )
A.40°
B.50°
C.65°
D.45°
10.如图所示,△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若∠DEF=55°,则∠A的度数是( )
A.35°
B.55°
C.70°
D.125°
二.填空题
11.如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,若以1cm为半径的⊙O与直线a相切,则OP的长为
.
12.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B=
.
13.若△ABC的三边长为3,4,5,则△ABC的外接圆半径R与内切圆半径r的差为
.
14.如图,AB是⊙O的直径,CD与⊙O相切于点C,∠BCD=25°,∠ABC=
°.
15.如图,等边△ABC中,CD为AB边上的高,⊙O与边AC、BC相切,当AB=4,OD=1时,⊙O的半径是
.
三.解答题
16.如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为点D,直线AC交⊙C于点E、F,且CF=AC
(1)求证:△ABF是直角三角形.
(2)若AC=6,则直接回答BF的长是多少.
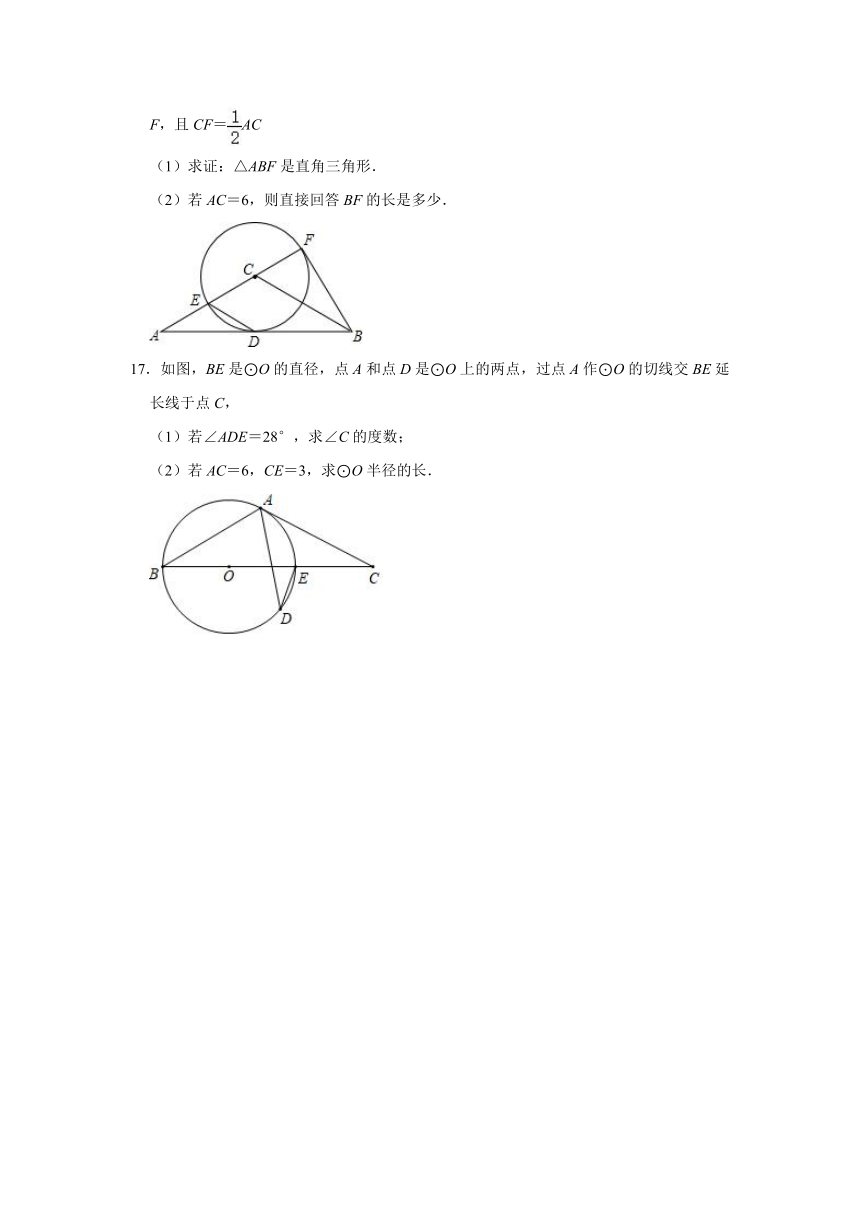
17.如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C,
(1)若∠ADE=28°,求∠C的度数;
(2)若AC=6,CE=3,求⊙O半径的长.
参考答案
1.解:∵⊙0的半径为6cm,点O到直线a的距离为6cm,
6=6,
∴⊙O与直线a的位置关系是相切,
故选:B.
2.解:∵AO,BO分别平分∠BAC,∠ABC,
∴点O是△ABC的内心.
故选:B.
3.解:如图,连接OB.
∵AB与⊙O相切于点B,
∴∠ABO=90°.
∵OB=OC,,
∴∠C=∠OBC,OB=OA,
∴∠A=30°,
∴∠AOB=60°,则∠C+∠OBC=60°,
∴∠C=30°.
故选:B.
4.解:∵PA是圆的切线.
∴∠OAP=90°
同理∠OBP=90°
根据四边形内角和定理可得:∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣60°=120°
故选:C.
5.解:∵圆心O到直线l的距离是4,等于⊙O的半径4,
∴直线l与⊙O相切.
故选:B.
6.解:∵直线l是⊙O的切线,
∴圆心O到直线l的距离等于圆的半径,
即圆心O到直线l的距离为5
故选:A.
7.
解:连接OA,
∵PA为⊙O的切线,
∴∠OAP=90°,
∵∠P=30°,
∴∠AOP=90°﹣∠P=90°﹣30°=60°,
∴∠ACB=∠AOP=30°,
故选:C.
8.解:如图:连接OB,
∵AB切⊙O于点B,
∴∠OBA=90°,
∵∠A=32°,
∴∠AOB=90°﹣34°=58°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=2∠C,
∴∠C=29°.
故选:A.
9.解:连接AO,
∵∠ADB=65°,
∴∠AOB=2∠ADB=130°,
∴∠AOC=50°,
∵AC是⊙O的切线,
∴∠OAC=90°,
∴∠C=90°﹣50°=40°,
故选:A.
10.解:连接OD,OF,OA,如下图所示,
∵△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,
∵∠DEF=55°,
∴∠DOF=2∠DEF=2×55°=110°(圆心角是圆周角的2倍),
∵在三角形AOD与三角形AOF中,
∵∠A+∠ADO+∠AFO+∠DOF=360°,
∵AD,AF是圆的切线,
∴∠ADO=∠AFO=90°,
∴∠A=360°﹣90°﹣90°﹣110°=70°,
故选:C.
11.解:∵直线a⊥b,O为直线b上一动点,
∴⊙O与直线a相切时,切点为H,
∴OH=1cm,
当点O在点H的左侧,⊙O与直线a相切时,如图1所示:
OP=PH﹣OH=4﹣1=3(cm);
当点O在点H的右侧,⊙O与直线a相切时,如图2所示:
OP=PH+OH=4+1=5(cm);
∴⊙O与直线a相切,OP的长为3cm或5cm,
故答案为:3cm或5cm.
12.解:∵PA切⊙O于点A,
∴∠OAP=90°,
∵∠P=36°,
∴∠AOP=54°,
∵=,
∴∠B=∠AOP=27°.
故答案为:27°.
13.解:
∵32+42=52,
∴△ABC为直角三角形,
∴斜边=5.
∴Rt△ABC的外接圆的半径为×5=2.5.
∵三角形ABC的面积=×三角形ABC的周长×内切圆半径,
∴×3×4=(3+4+5)r.
解得:r=1.
∴△ABC的外接圆半径R与内切圆半径r的差=2.5﹣1=
故答案为:.
14.解:连接OC,如图,
∵CD切⊙O于点C,
∴OC⊥CD,
∴∠OCD=90°,
∴∠OCB=90°﹣∠BCD=90°﹣25°=65°,
∵OB=OC,
∴∠B=∠OCB=65°.
故答案为:65.
15.解:如图,设图中圆O与BC的切点为M,
连接OM,
则OM⊥MC,
∴∠OMC=90°,
依题意知,∠DCB=30°,
∵CD⊥AB,AB=4,
∴∠CDB=90°,BD=2,
∴CD=BD=6,
∵OD=1,
∴OC=5,
∴OM=OC=,
故答案为:.
16.(1)证明:如图,连接CD,
则CF=CD,
∵AB是⊙C的切线.
∴CD⊥AB,∠ADC=∠BDC=90°,
在Rt△ACD中,
∵CF=,
∴CD=CF=,
∴∠A=30°
∵AC=BC∴∠ABC=∠A=30°,
∴∠ACB=120°,
∠BCD=∠BCF=60°,
又∵BC=BC,
∴△BCD≌△BCF(SAS),
∴∠BFC=∠BDC=90°,
∴△ABF是直角三角形.
(2)解:∵AC=BC,CD⊥AB,
∴AD=BD=BF,
在Rt△ACD中,∵∠A=30°,AC=6,
∴CD=AC=3,
∴AD=CD=3.
∴BF=3.
17.解:(1)如图,连接OA,
∵∠ADE=28°,
∴由圆周角定理得:∠AOC=2∠ADE=56°,
∵AC切⊙O于A,
∴∠OAC=90°,
∴∠C=180°﹣∠AOC﹣∠OAC=180°﹣56°﹣90°=34°;
(2)设OA=OE=r,
在Rt△OAC中,由勾股定理得:OA2+AC2=OC2,
即r2+62=(r+3)2,
解得:r=,
答:⊙O半径的长是.
同步习题
一.选择题
1.已知⊙O的半径为6cm,圆心O到直线a的距离为6cm,则直线a与⊙O的位置关系为( )
A.相交
B.相切
C.相离
D.无法确定
2.如图,在△ABC中,AO,BO分别平分∠BAC,∠ABC,则点O是△ABC的( )
A.外心
B.内心
C.中线交点
D.高线交点
3.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC,若OC=OA,则∠C等于( )
A.15°
B.30°
C.45°
D.60°
4.如图,PA、PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
A.60°
B.90°
C.120°
D.150°
5.已知⊙O的半径为4,圆心O到直线l的距离是4,则⊙O与直线l的关系是( )
A.相交
B.相切
C.相离
D.相交或相切
6.已知⊙O的半径是5,直线l是⊙O的切线,则圆心O到直线l的距离是( )
A.5
B.2.5
C.3
D.10
7.如图,PA是⊙O的切线,点A为切点,PO交⊙O于点B,∠P=30°,点C在⊙O上,连接AC,BC,则∠ACB的度数为( )
A.25°
B.28°
C.30°
D.35°
8.如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=32°,则∠ACB的度数是( )
A.29°
B.30°
C.31°
D.32°
9.如图,在△ABC中,O是BC边上的点,以点O为圆心,BO为半径的⊙O与AC相切于点A,D是优弧AB上一点,∠ADB=65°,则∠C的度数是( )
A.40°
B.50°
C.65°
D.45°
10.如图所示,△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若∠DEF=55°,则∠A的度数是( )
A.35°
B.55°
C.70°
D.125°
二.填空题
11.如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,若以1cm为半径的⊙O与直线a相切,则OP的长为
.
12.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B=
.
13.若△ABC的三边长为3,4,5,则△ABC的外接圆半径R与内切圆半径r的差为
.
14.如图,AB是⊙O的直径,CD与⊙O相切于点C,∠BCD=25°,∠ABC=
°.
15.如图,等边△ABC中,CD为AB边上的高,⊙O与边AC、BC相切,当AB=4,OD=1时,⊙O的半径是
.
三.解答题
16.如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为点D,直线AC交⊙C于点E、F,且CF=AC
(1)求证:△ABF是直角三角形.
(2)若AC=6,则直接回答BF的长是多少.
17.如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C,
(1)若∠ADE=28°,求∠C的度数;
(2)若AC=6,CE=3,求⊙O半径的长.
参考答案
1.解:∵⊙0的半径为6cm,点O到直线a的距离为6cm,
6=6,
∴⊙O与直线a的位置关系是相切,
故选:B.
2.解:∵AO,BO分别平分∠BAC,∠ABC,
∴点O是△ABC的内心.
故选:B.
3.解:如图,连接OB.
∵AB与⊙O相切于点B,
∴∠ABO=90°.
∵OB=OC,,
∴∠C=∠OBC,OB=OA,
∴∠A=30°,
∴∠AOB=60°,则∠C+∠OBC=60°,
∴∠C=30°.
故选:B.
4.解:∵PA是圆的切线.
∴∠OAP=90°
同理∠OBP=90°
根据四边形内角和定理可得:∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣60°=120°
故选:C.
5.解:∵圆心O到直线l的距离是4,等于⊙O的半径4,
∴直线l与⊙O相切.
故选:B.
6.解:∵直线l是⊙O的切线,
∴圆心O到直线l的距离等于圆的半径,
即圆心O到直线l的距离为5
故选:A.
7.
解:连接OA,
∵PA为⊙O的切线,
∴∠OAP=90°,
∵∠P=30°,
∴∠AOP=90°﹣∠P=90°﹣30°=60°,
∴∠ACB=∠AOP=30°,
故选:C.
8.解:如图:连接OB,
∵AB切⊙O于点B,
∴∠OBA=90°,
∵∠A=32°,
∴∠AOB=90°﹣34°=58°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=2∠C,
∴∠C=29°.
故选:A.
9.解:连接AO,
∵∠ADB=65°,
∴∠AOB=2∠ADB=130°,
∴∠AOC=50°,
∵AC是⊙O的切线,
∴∠OAC=90°,
∴∠C=90°﹣50°=40°,
故选:A.
10.解:连接OD,OF,OA,如下图所示,
∵△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,
∵∠DEF=55°,
∴∠DOF=2∠DEF=2×55°=110°(圆心角是圆周角的2倍),
∵在三角形AOD与三角形AOF中,
∵∠A+∠ADO+∠AFO+∠DOF=360°,
∵AD,AF是圆的切线,
∴∠ADO=∠AFO=90°,
∴∠A=360°﹣90°﹣90°﹣110°=70°,
故选:C.
11.解:∵直线a⊥b,O为直线b上一动点,
∴⊙O与直线a相切时,切点为H,
∴OH=1cm,
当点O在点H的左侧,⊙O与直线a相切时,如图1所示:
OP=PH﹣OH=4﹣1=3(cm);
当点O在点H的右侧,⊙O与直线a相切时,如图2所示:
OP=PH+OH=4+1=5(cm);
∴⊙O与直线a相切,OP的长为3cm或5cm,
故答案为:3cm或5cm.
12.解:∵PA切⊙O于点A,
∴∠OAP=90°,
∵∠P=36°,
∴∠AOP=54°,
∵=,
∴∠B=∠AOP=27°.
故答案为:27°.
13.解:
∵32+42=52,
∴△ABC为直角三角形,
∴斜边=5.
∴Rt△ABC的外接圆的半径为×5=2.5.
∵三角形ABC的面积=×三角形ABC的周长×内切圆半径,
∴×3×4=(3+4+5)r.
解得:r=1.
∴△ABC的外接圆半径R与内切圆半径r的差=2.5﹣1=
故答案为:.
14.解:连接OC,如图,
∵CD切⊙O于点C,
∴OC⊥CD,
∴∠OCD=90°,
∴∠OCB=90°﹣∠BCD=90°﹣25°=65°,
∵OB=OC,
∴∠B=∠OCB=65°.
故答案为:65.
15.解:如图,设图中圆O与BC的切点为M,
连接OM,
则OM⊥MC,
∴∠OMC=90°,
依题意知,∠DCB=30°,
∵CD⊥AB,AB=4,
∴∠CDB=90°,BD=2,
∴CD=BD=6,
∵OD=1,
∴OC=5,
∴OM=OC=,
故答案为:.
16.(1)证明:如图,连接CD,
则CF=CD,
∵AB是⊙C的切线.
∴CD⊥AB,∠ADC=∠BDC=90°,
在Rt△ACD中,
∵CF=,
∴CD=CF=,
∴∠A=30°
∵AC=BC∴∠ABC=∠A=30°,
∴∠ACB=120°,
∠BCD=∠BCF=60°,
又∵BC=BC,
∴△BCD≌△BCF(SAS),
∴∠BFC=∠BDC=90°,
∴△ABF是直角三角形.
(2)解:∵AC=BC,CD⊥AB,
∴AD=BD=BF,
在Rt△ACD中,∵∠A=30°,AC=6,
∴CD=AC=3,
∴AD=CD=3.
∴BF=3.
17.解:(1)如图,连接OA,
∵∠ADE=28°,
∴由圆周角定理得:∠AOC=2∠ADE=56°,
∵AC切⊙O于A,
∴∠OAC=90°,
∴∠C=180°﹣∠AOC﹣∠OAC=180°﹣56°﹣90°=34°;
(2)设OA=OE=r,
在Rt△OAC中,由勾股定理得:OA2+AC2=OC2,
即r2+62=(r+3)2,
解得:r=,
答:⊙O半径的长是.
同课章节目录
