2020-2021学年九年级数学北师大版3.2用频率估计概率同步练习(Word版 含答案)
文档属性
| 名称 | 2020-2021学年九年级数学北师大版3.2用频率估计概率同步练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 246.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 00:06:22 | ||
图片预览



文档简介
第2节
用频率估计概率
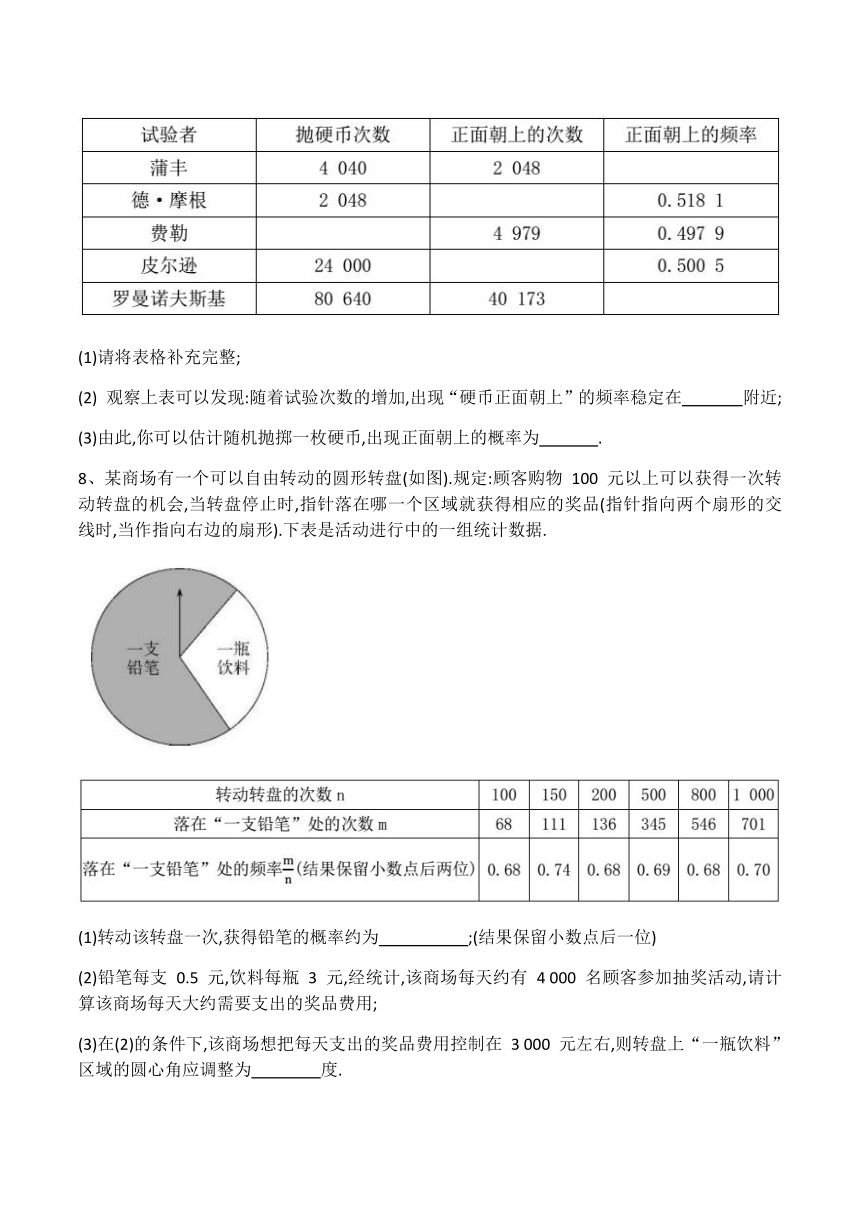
1、小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表:
若抛掷硬币的次数为
1
000,则“正面朝上”的频数最接近(
)
A.
200
B.
300
C.
500
D.
800
2、在一个不透明的布袋中,共有
30
个小球,除颜色外其他完全相同.若每次将球搅匀后摸一个球记下颜色后再放回布袋.通过大量重复摸球试验后发现,摸到红色球的频率稳定在
0.2
左右,则布袋中红色球的个数应该是(
)
A.
6
B.
15
C.
24
D.
12
3、下表显示的是某种大豆在相同条件下的发芽试验结果:
①当
n
为
400
时,大豆发芽的粒数为
382,发芽的频率为
0.955,所以大豆发芽的概率是
0.955;
②试验时随着大豆粒数的增加,大豆发芽的频率总在
0.95
附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是
0.95;
③若大豆的粒数
n
为
4
000,则大豆发芽的粒数大约为
3
800.
其中推断合理的是(
)
A.
①②③
B.
①②
C.
①③
D.
②③
4、某学习小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是(
)
A.
掷一枚质地均匀的正六面体骰子,出现
1
点朝上
B.
任意写一个整数,它能被
2
整除
C.
不透明袋中装有大小和质地都相同的1
个红球和
2
个黄球,从中随机取一个球,取到红球
D.
先后两次掷一枚质地均匀的硬币,两次都出现反面
5、“六一”期间,小洁的妈妈经营的玩具店进了一纸箱除颜色外都相同的散装塑料球共
1000
个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下其颜色,再把它放回纸箱中;搅匀后再随机摸出一个球记下其颜色,再把它放回纸箱中;……,多次重复上述过程后,发现摸到红球的频率逐渐稳定在
0.2
左右,由此可以估计纸箱内红球的个数是
.
6、下表显示了同学们用计算机模拟随机投针试验的某次试验的结果.
下面有三个推断:
①投掷
1
000
次时,针与直线相交的次数是
454,则针与直线相交的概率是
0.454;
②随着试验次数的增加,针与直线相交的频率总在
0.477
附近摆动,显示出一定的稳定性,可以估计针与直线相交的概率是
0.477;
③若再次用计算机模拟此试验,则当投掷次数为
10
000
时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是
.
7、下表给出了一些著名科学家做抛硬币试验的部分资料,请按要求完成下列问题:
(1)请将表格补充完整;
(2)
观察上表可以发现:随着试验次数的增加,出现“硬币正面朝上”的频率稳定在
附近;
(3)由此,你可以估计随机抛掷一枚硬币,出现正面朝上的概率为
.
8、某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物
100
元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据.
(1)转动该转盘一次,获得铅笔的概率约为
;(结果保留小数点后一位)
(2)铅笔每支
0.5
元,饮料每瓶
3
元,经统计,该商场每天约有
4
000
名顾客参加抽奖活动,请计算该商场每天大约需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在
3
000
元左右,则转盘上“一瓶饮料”区域的圆心角应调整为
度.
9、4
件同型号的产品中,有
1
件不合格品和
3
件合格品.
(1)从这
4
件产品中随机抽取
1
件进行检测,求抽到的是不合格品的概率;
(2)从这
4
件产品中随机抽取
2
件进行检测,求抽到的都是合格品的概率;
(3)在这
4
件产品中加入
x
件合格品后,进行如下试验:随机抽取
1
件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在
0.95,则可以推算出
x的值大约是多少.
10、某同学发现操场中有一个不规则的封闭图形,如图所示,为了知道它的面积,他在封闭图形内画出了一个半径为
1
米的圆,在不远处向圆内掷石子,结果记录如下:
请根据以上信息,回答问题:
(1)估计石子落在圆内(含圆上)的概率;
(2)估计封闭图形的面积.
答案
1.C
2.A
3.D
4.C
5.
200
6.
②
7.
(1)从上到下空白处依次填:0.5069;1061;10000;12012;0.4982.
(2)0.5
(3)0.5
8.
(1)转动该转盘一次,获得铅笔的概率约为
0.7.
(2)4
000×0.5×0.7+4
000×3×0.3=5
000(元),所以该商场每天大约需要支出的奖品费用为
5
000
元.
(3)设转盘上“一瓶饮料”区域的圆心角应调整为
n
度,则
4
000×3×+4
000×0.5×(1-
)=3
000,解得
n=36,所以转盘上“一瓶饮料”区域的圆心角应调整为
36
度.
9.
(1)∵4
件同型号的产品中,有
1
件不合格品,∴P(抽到的是不合格品)=.
(2)设不合格产品为甲,合格产品为乙、丙、丁,则随机抽取
2
件的情况有甲乙,甲丙,甲丁,
乙丙,乙丁,丙丁,共
6
种情况.其中,合格的有
3
种情况,∴P(抽到的都是合格品)==.
(3)∵大量重复试验后发现,抽到合格品的频率稳定在0.95,∴估计抽到合格品的概率等于
0.95,∴=0.95,解得
x=16.经检验,x=16
是分式方程的解,且符合题意.
10.
(1)≈0.378,≈0.321,=,=.
随着投掷次数的增大,石子落在圆内(含圆上)的频率稳定在附近,故估计石子落在圆内(含圆上)的概率为.
(2)设封闭图形的面积为
a
平方米,根据题意得=,解得
a=3π,经检验,a=3π
是分式方程的解.
答:估计封闭图形的面积为
3π
平方米.
6
用频率估计概率
1、小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表:
若抛掷硬币的次数为
1
000,则“正面朝上”的频数最接近(
)
A.
200
B.
300
C.
500
D.
800
2、在一个不透明的布袋中,共有
30
个小球,除颜色外其他完全相同.若每次将球搅匀后摸一个球记下颜色后再放回布袋.通过大量重复摸球试验后发现,摸到红色球的频率稳定在
0.2
左右,则布袋中红色球的个数应该是(
)
A.
6
B.
15
C.
24
D.
12
3、下表显示的是某种大豆在相同条件下的发芽试验结果:
①当
n
为
400
时,大豆发芽的粒数为
382,发芽的频率为
0.955,所以大豆发芽的概率是
0.955;
②试验时随着大豆粒数的增加,大豆发芽的频率总在
0.95
附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是
0.95;
③若大豆的粒数
n
为
4
000,则大豆发芽的粒数大约为
3
800.
其中推断合理的是(
)
A.
①②③
B.
①②
C.
①③
D.
②③
4、某学习小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是(
)
A.
掷一枚质地均匀的正六面体骰子,出现
1
点朝上
B.
任意写一个整数,它能被
2
整除
C.
不透明袋中装有大小和质地都相同的1
个红球和
2
个黄球,从中随机取一个球,取到红球
D.
先后两次掷一枚质地均匀的硬币,两次都出现反面
5、“六一”期间,小洁的妈妈经营的玩具店进了一纸箱除颜色外都相同的散装塑料球共
1000
个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下其颜色,再把它放回纸箱中;搅匀后再随机摸出一个球记下其颜色,再把它放回纸箱中;……,多次重复上述过程后,发现摸到红球的频率逐渐稳定在
0.2
左右,由此可以估计纸箱内红球的个数是
.
6、下表显示了同学们用计算机模拟随机投针试验的某次试验的结果.
下面有三个推断:
①投掷
1
000
次时,针与直线相交的次数是
454,则针与直线相交的概率是
0.454;
②随着试验次数的增加,针与直线相交的频率总在
0.477
附近摆动,显示出一定的稳定性,可以估计针与直线相交的概率是
0.477;
③若再次用计算机模拟此试验,则当投掷次数为
10
000
时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是
.
7、下表给出了一些著名科学家做抛硬币试验的部分资料,请按要求完成下列问题:
(1)请将表格补充完整;
(2)
观察上表可以发现:随着试验次数的增加,出现“硬币正面朝上”的频率稳定在
附近;
(3)由此,你可以估计随机抛掷一枚硬币,出现正面朝上的概率为
.
8、某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物
100
元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据.
(1)转动该转盘一次,获得铅笔的概率约为
;(结果保留小数点后一位)
(2)铅笔每支
0.5
元,饮料每瓶
3
元,经统计,该商场每天约有
4
000
名顾客参加抽奖活动,请计算该商场每天大约需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在
3
000
元左右,则转盘上“一瓶饮料”区域的圆心角应调整为
度.
9、4
件同型号的产品中,有
1
件不合格品和
3
件合格品.
(1)从这
4
件产品中随机抽取
1
件进行检测,求抽到的是不合格品的概率;
(2)从这
4
件产品中随机抽取
2
件进行检测,求抽到的都是合格品的概率;
(3)在这
4
件产品中加入
x
件合格品后,进行如下试验:随机抽取
1
件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在
0.95,则可以推算出
x的值大约是多少.
10、某同学发现操场中有一个不规则的封闭图形,如图所示,为了知道它的面积,他在封闭图形内画出了一个半径为
1
米的圆,在不远处向圆内掷石子,结果记录如下:
请根据以上信息,回答问题:
(1)估计石子落在圆内(含圆上)的概率;
(2)估计封闭图形的面积.
答案
1.C
2.A
3.D
4.C
5.
200
6.
②
7.
(1)从上到下空白处依次填:0.5069;1061;10000;12012;0.4982.
(2)0.5
(3)0.5
8.
(1)转动该转盘一次,获得铅笔的概率约为
0.7.
(2)4
000×0.5×0.7+4
000×3×0.3=5
000(元),所以该商场每天大约需要支出的奖品费用为
5
000
元.
(3)设转盘上“一瓶饮料”区域的圆心角应调整为
n
度,则
4
000×3×+4
000×0.5×(1-
)=3
000,解得
n=36,所以转盘上“一瓶饮料”区域的圆心角应调整为
36
度.
9.
(1)∵4
件同型号的产品中,有
1
件不合格品,∴P(抽到的是不合格品)=.
(2)设不合格产品为甲,合格产品为乙、丙、丁,则随机抽取
2
件的情况有甲乙,甲丙,甲丁,
乙丙,乙丁,丙丁,共
6
种情况.其中,合格的有
3
种情况,∴P(抽到的都是合格品)==.
(3)∵大量重复试验后发现,抽到合格品的频率稳定在0.95,∴估计抽到合格品的概率等于
0.95,∴=0.95,解得
x=16.经检验,x=16
是分式方程的解,且符合题意.
10.
(1)≈0.378,≈0.321,=,=.
随着投掷次数的增大,石子落在圆内(含圆上)的频率稳定在附近,故估计石子落在圆内(含圆上)的概率为.
(2)设封闭图形的面积为
a
平方米,根据题意得=,解得
a=3π,经检验,a=3π
是分式方程的解.
答:估计封闭图形的面积为
3π
平方米.
6
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
