人教版数学九年级上册24.1.4 圆周角的概念和圆周角的定理课件(17张)
文档属性
| 名称 | 人教版数学九年级上册24.1.4 圆周角的概念和圆周角的定理课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 00:00:00 | ||
图片预览




文档简介
24.1.4 圆周角的概念和圆周角定理
一、复习引入:
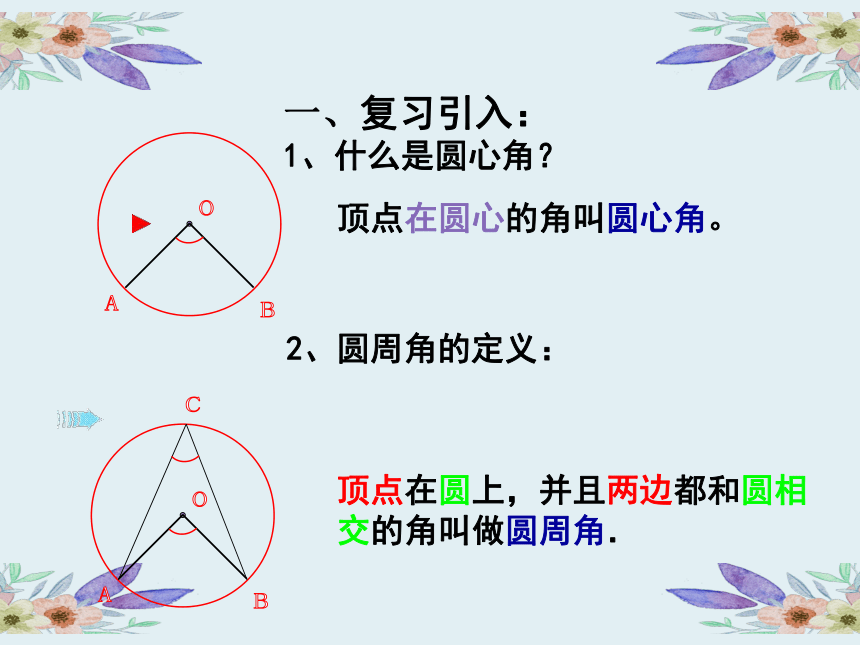
1、什么是圆心角?
o
A
B
顶点在圆心的角叫圆心角。
o
A
B
C
2、圆周角的定义:
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
3、慧眼识图:
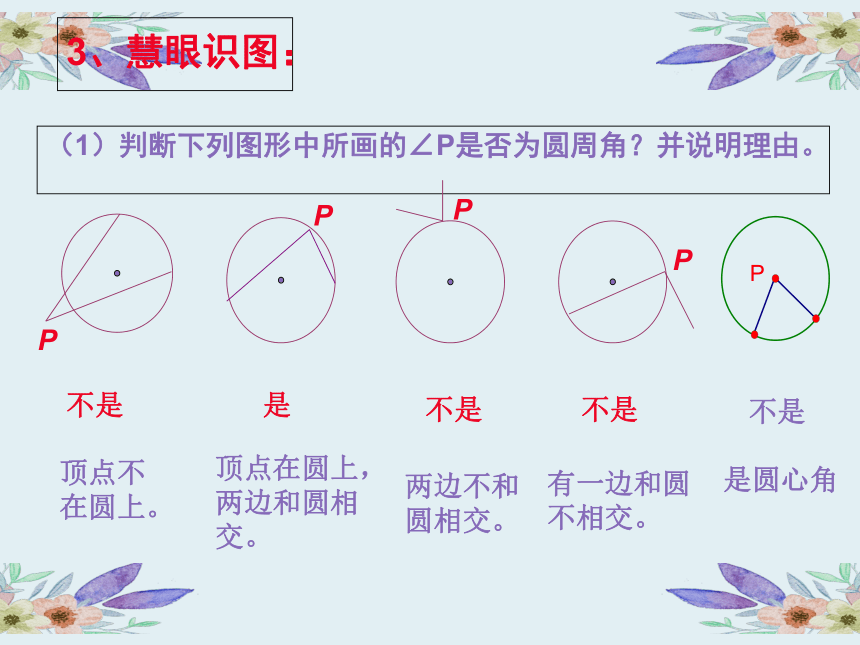
(1)判断下列图形中所画的∠P是否为圆周角?并说明理由。
P
P
P
不是
是
不是
不是
顶点不在圆上。
顶点在圆上,两边和圆相交。
两边不和圆相交。
有一边和圆不相交。
P
不是
是圆心角
(2)图1中有几个圆周角?( )
A、2个, B、3个, C、4个, D、5个。
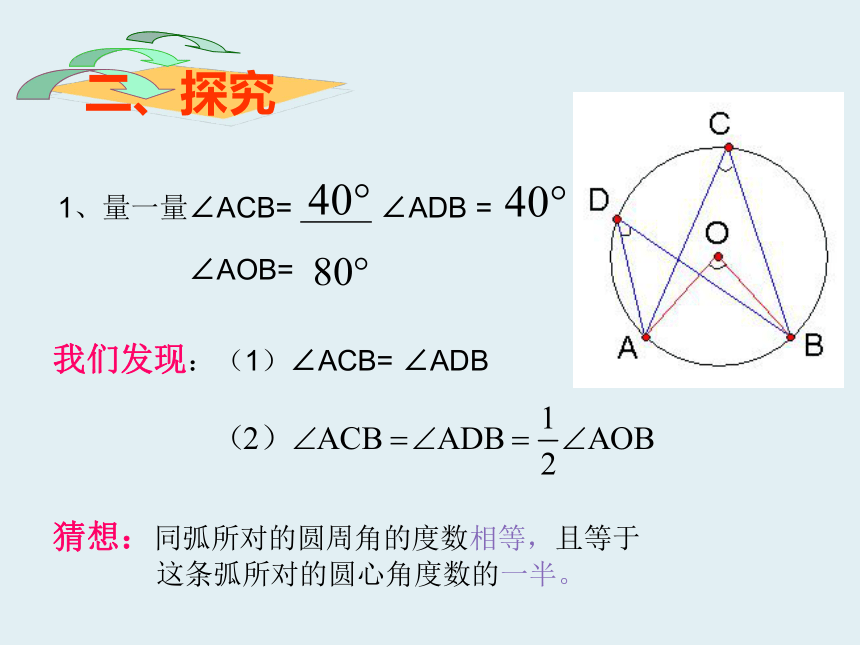
我们发现:(1)∠ACB= ∠ADB
1、量一量∠ACB= ∠ADB =
∠AOB=
猜想:同弧所对的圆周角的度数相等,且等于
这条弧所对的圆心角度数的一半。
二、探究
(1)由演示我们可得圆心与圆周角有三种位置关系
A
B
o
C
o
A
B
C
o
A
B
C
圆心在一边上
圆心在角内
圆心在角外
2、证明(几何画板演示)
同弧所对的圆周角相等,且都等于它所对的圆心角的一半。
你能证明吗?
已知:在⊙O中,BC所对的圆周角是∠BAC,圆心角是
∠BOC。求证: ∠BAC= ∠BOC
︵
A
O
C
B
(1)
A
O
C
B
(2)
A
O
C
B
(3)
证明:
分三种情况讨论:
(1)圆心O在∠BAC的一边上。
OA=OC
∠C=∠BAC
∠BOC=∠C+∠BAC
∠BAC= ∠BOC
已知:在⊙O中,BC所对的圆周角是∠BAC,圆心角是
∠BOC。求证: ∠BAC= ∠BOC
︵
A
O
C
B
(1)
A
O
C
B
(2)
A
O
C
B
(3)
D
E
同条弧所对的圆周角相等,且都等于它所对的圆心角的一半。
如图:
圆周角的定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
结论:
几何语言:
在⊙O中
1、如图,在⊙O中, ∠AOC=100°,则等于∠ABC为( )
A、50°; B、80°; C、90°; D、100°
跟踪训练
B
A
C
O
A
2、如图d,已知∠ACB = 20?,则∠AOB = _____。
O
B
A
C
图d
40?
3、如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?(注意:同弧所对的圆周角相等)
∠8= ∠5
∠2 = ∠7
∠1 = ∠4
∠3 = ∠6
跟踪训练
问题1:如图,AB是⊙O的直径,请问:
∠C1、∠C2、∠C3的度数是 。
推论:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
问题2: 若∠C1、∠C2、∠C3是直角,那么∠AOB是 。
90°
180°
探究与思考:
几何语言:
在⊙O中∵AB是直径
∴ ∠C1=∠C2=∠C3= 90°
在⊙O中∵ ∠C1= 90°
∴AB是直径
(1)如图(a),AB是⊙O的直径,AC=BC,则∠A= °。
跟踪训练
(2)如图(b),AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为 。
45
75°
(3)如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平
分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
跟踪训练
今天我们收获了什么?
课堂小结
作业:教材P87 第2、4题。
结束寄语
不学自知,不问自晓,古今行事,未之有也.
下课了!
再见
一、复习引入:
1、什么是圆心角?
o
A
B
顶点在圆心的角叫圆心角。
o
A
B
C
2、圆周角的定义:
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
3、慧眼识图:
(1)判断下列图形中所画的∠P是否为圆周角?并说明理由。
P
P
P
不是
是
不是
不是
顶点不在圆上。
顶点在圆上,两边和圆相交。
两边不和圆相交。
有一边和圆不相交。
P
不是
是圆心角
(2)图1中有几个圆周角?( )
A、2个, B、3个, C、4个, D、5个。
我们发现:(1)∠ACB= ∠ADB
1、量一量∠ACB= ∠ADB =
∠AOB=
猜想:同弧所对的圆周角的度数相等,且等于
这条弧所对的圆心角度数的一半。
二、探究
(1)由演示我们可得圆心与圆周角有三种位置关系
A
B
o
C
o
A
B
C
o
A
B
C
圆心在一边上
圆心在角内
圆心在角外
2、证明(几何画板演示)
同弧所对的圆周角相等,且都等于它所对的圆心角的一半。
你能证明吗?
已知:在⊙O中,BC所对的圆周角是∠BAC,圆心角是
∠BOC。求证: ∠BAC= ∠BOC
︵
A
O
C
B
(1)
A
O
C
B
(2)
A
O
C
B
(3)
证明:
分三种情况讨论:
(1)圆心O在∠BAC的一边上。
OA=OC
∠C=∠BAC
∠BOC=∠C+∠BAC
∠BAC= ∠BOC
已知:在⊙O中,BC所对的圆周角是∠BAC,圆心角是
∠BOC。求证: ∠BAC= ∠BOC
︵
A
O
C
B
(1)
A
O
C
B
(2)
A
O
C
B
(3)
D
E
同条弧所对的圆周角相等,且都等于它所对的圆心角的一半。
如图:
圆周角的定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
结论:
几何语言:
在⊙O中
1、如图,在⊙O中, ∠AOC=100°,则等于∠ABC为( )
A、50°; B、80°; C、90°; D、100°
跟踪训练
B
A
C
O
A
2、如图d,已知∠ACB = 20?,则∠AOB = _____。
O
B
A
C
图d
40?
3、如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?(注意:同弧所对的圆周角相等)
∠8= ∠5
∠2 = ∠7
∠1 = ∠4
∠3 = ∠6
跟踪训练
问题1:如图,AB是⊙O的直径,请问:
∠C1、∠C2、∠C3的度数是 。
推论:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
问题2: 若∠C1、∠C2、∠C3是直角,那么∠AOB是 。
90°
180°
探究与思考:
几何语言:
在⊙O中∵AB是直径
∴ ∠C1=∠C2=∠C3= 90°
在⊙O中∵ ∠C1= 90°
∴AB是直径
(1)如图(a),AB是⊙O的直径,AC=BC,则∠A= °。
跟踪训练
(2)如图(b),AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为 。
45
75°
(3)如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平
分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
跟踪训练
今天我们收获了什么?
课堂小结
作业:教材P87 第2、4题。
结束寄语
不学自知,不问自晓,古今行事,未之有也.
下课了!
再见
同课章节目录
