人教版九年级数学上册22.2 二次函数与一元二次方程课件(共20张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.2 二次函数与一元二次方程课件(共20张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 00:00:00 | ||
图片预览




文档简介
22.2 二次函数与一元二次方程
【例题】以 40 m/s 的速度将小球沿与地面成 30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度 h (单位:m )与飞行时间t(单位:s)之间具有函数关系 h = 20t - 5t 2.
(1)小球的飞行高度能否达到 15 m? 如果能,需要多少飞行时间?
知识点 1
二次函数与一元二次方程的关系
一、自学生疑
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
O
h
t
15
1
3
∴当球飞行1s或3s时,它的高度为15m.
解:15=20t-5t2,
t2-4t+3=0,
t1=1,t2=3.
你能结合上图,指出为什么在两个时间求的高度为15m吗?
函数关系 h = 20t - 5t 2.
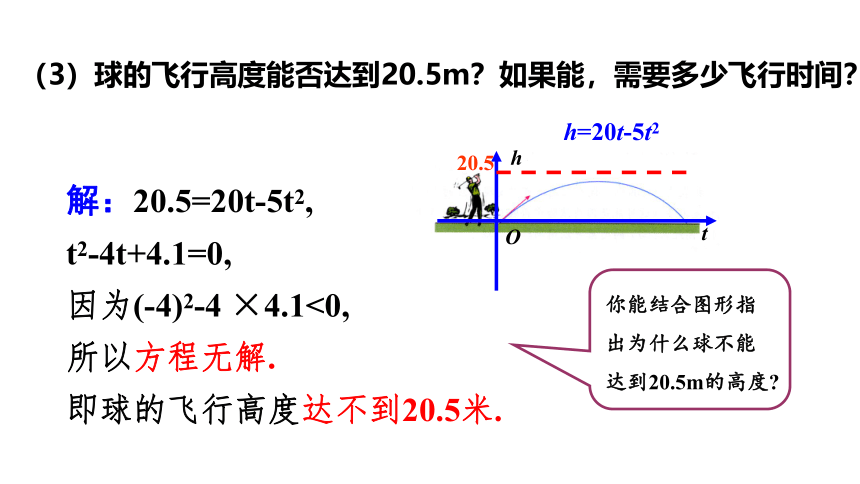
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
你能结合图形指出为什么只在一个时间球的高度为20m?
O
h
t
20
4
20=20t-5t2,
t2-4t+4=0,
t1=t2=2.
当球飞行2秒时,它的高度为20米.
h=20t-5t2
解:
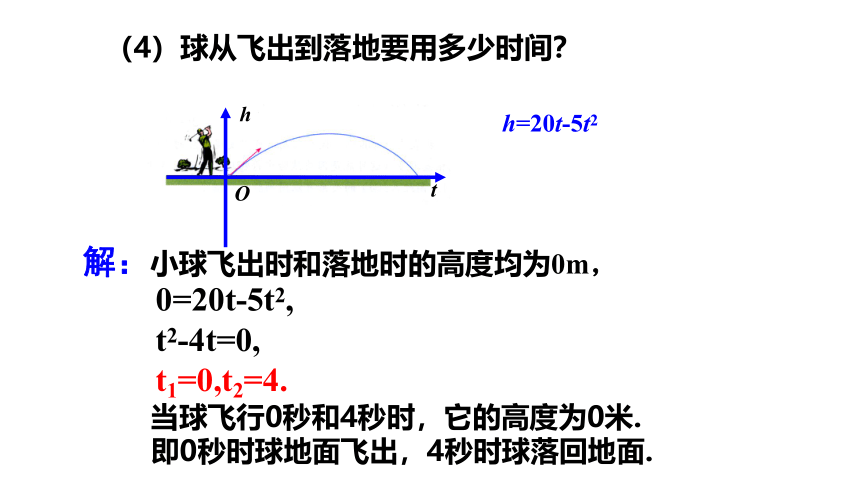
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
O
h
t
你能结合图形指出为什么球不能达到20.5m的高度?
20.5
解:20.5=20t-5t2,
t2-4t+4.1=0,
因为(-4)2-4 ×4.1<0,
所以方程无解.
即球的飞行高度达不到20.5米.
h=20t-5t2
(4)球从飞出到落地要用多少时间?
O
h
t
0=20t-5t2,
t2-4t=0,
t1=0,t2=4.
当球飞行0秒和4秒时,它的高度为0米.
即0秒时球地面飞出,4秒时球落回地面.
h=20t-5t2
解:小球飞出时和落地时的高度均为0m,
从上面发现,二次函数y=ax2+bx+c何时为一元二次方程?
?
如:y=5时,则5=ax2+bx+c就是一个一元二次方程.
为一个常数
(定值)
二、合作探究
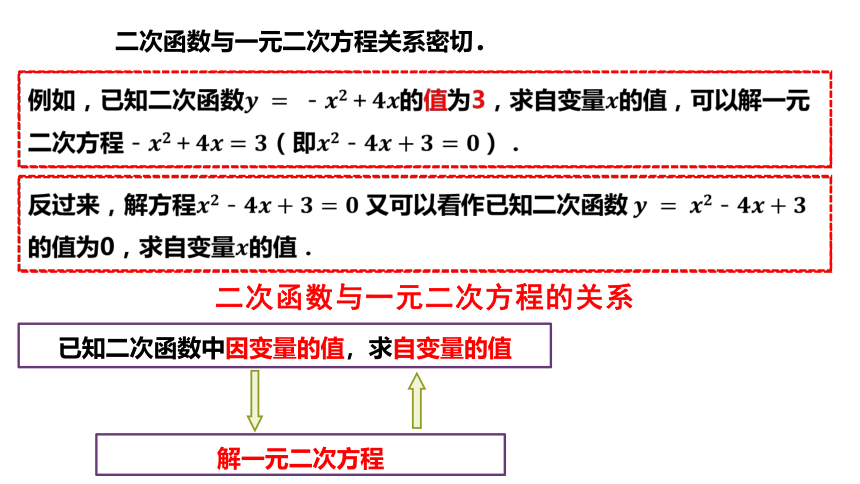
二次函数与一元二次方程关系密切.
?
?
二次函数与一元二次方程的关系
已知二次函数中因变量的值,求自变量的值
解一元二次方程
?
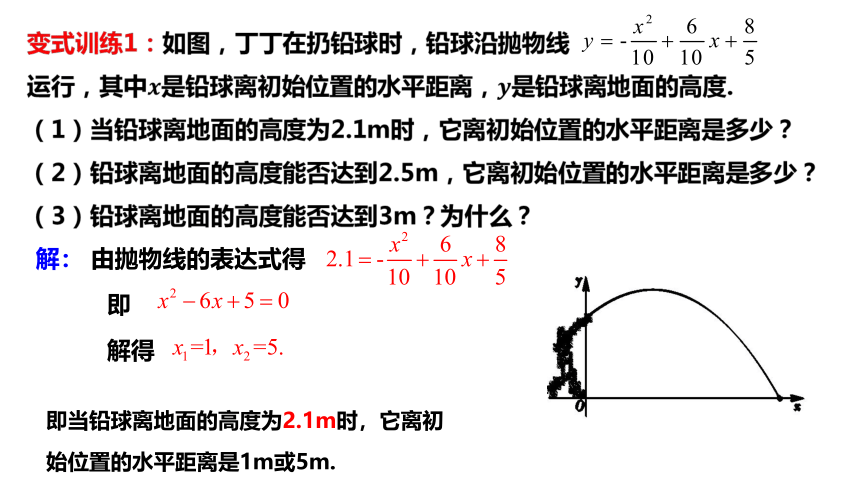
解: 由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.1m时,它离初始位置的水平距离是1m或5m.
?
由抛物线的表达式得
即
解得
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距 离是多少?
即当铅球离地面的高度为2.5m时,它离初始位置的水平距离是3m.
(3)铅球离地面的高度能否达到3m?为什么?
∴方程无实根.
利用二次函数与x轴的交点讨论一元二次方程的根的情况
【思考】观察思考下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗?
(1)y=x2+x-2; (2)y=x2-6x+9; (3)y=x2-x+1.
知识 2
二次函数图象与x轴的公共点的横坐标是多少?
无公共点
先画出函数图象:
对应一元二次方程的根是多少?
x1 =-2,
x2 =1.
x1 =x2 =3.
方程无解
?
有两个不等实根
有两个相等实根
没有实数根
有两个交点
有一个交点
没有交点
△ > 0
△ = 0
△ < 0
?
抛物线 y=ax2+bx+c与x轴
若抛物线 y=ax2+bx+c 与 x 轴有交点,则
b2 – 4ac ≥ 0
△= b2 – 4ac
二次函数与一元二次方程的关系(2)
?
?
1. 若一元二次方程 无实根,则抛物线 图象位于( )
A.x轴上方 B.第一、二、三象限
C.x轴下方 D.第二、三、四象限
A
三、训练总结
2. 二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3 B.k<3且k≠0
C.k≤3 D.k≤3且k≠0
D
三、训练总结
3.若二次函数y=-x2+2x+k的部分图象如图所示,且关于x的一元二次方程-x2+2x+k=0的一个解x1=3,则另一个解x2= ;
-1
y
O
x
1
3
4. 一元二次方程 3x2+x-10=0的两个根是x1=-2 ,x2= ,那么二次函数 y= 3x2+x-10与x轴的交点坐标是 .
(-2,0) ( ,0)
某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面 米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
能力拓展
四、评点小结
【例题】以 40 m/s 的速度将小球沿与地面成 30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度 h (单位:m )与飞行时间t(单位:s)之间具有函数关系 h = 20t - 5t 2.
(1)小球的飞行高度能否达到 15 m? 如果能,需要多少飞行时间?
知识点 1
二次函数与一元二次方程的关系
一、自学生疑
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
O
h
t
15
1
3
∴当球飞行1s或3s时,它的高度为15m.
解:15=20t-5t2,
t2-4t+3=0,
t1=1,t2=3.
你能结合上图,指出为什么在两个时间求的高度为15m吗?
函数关系 h = 20t - 5t 2.
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
你能结合图形指出为什么只在一个时间球的高度为20m?
O
h
t
20
4
20=20t-5t2,
t2-4t+4=0,
t1=t2=2.
当球飞行2秒时,它的高度为20米.
h=20t-5t2
解:
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
O
h
t
你能结合图形指出为什么球不能达到20.5m的高度?
20.5
解:20.5=20t-5t2,
t2-4t+4.1=0,
因为(-4)2-4 ×4.1<0,
所以方程无解.
即球的飞行高度达不到20.5米.
h=20t-5t2
(4)球从飞出到落地要用多少时间?
O
h
t
0=20t-5t2,
t2-4t=0,
t1=0,t2=4.
当球飞行0秒和4秒时,它的高度为0米.
即0秒时球地面飞出,4秒时球落回地面.
h=20t-5t2
解:小球飞出时和落地时的高度均为0m,
从上面发现,二次函数y=ax2+bx+c何时为一元二次方程?
?
如:y=5时,则5=ax2+bx+c就是一个一元二次方程.
为一个常数
(定值)
二、合作探究
二次函数与一元二次方程关系密切.
?
?
二次函数与一元二次方程的关系
已知二次函数中因变量的值,求自变量的值
解一元二次方程
?
解: 由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.1m时,它离初始位置的水平距离是1m或5m.
?
由抛物线的表达式得
即
解得
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距 离是多少?
即当铅球离地面的高度为2.5m时,它离初始位置的水平距离是3m.
(3)铅球离地面的高度能否达到3m?为什么?
∴方程无实根.
利用二次函数与x轴的交点讨论一元二次方程的根的情况
【思考】观察思考下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗?
(1)y=x2+x-2; (2)y=x2-6x+9; (3)y=x2-x+1.
知识 2
二次函数图象与x轴的公共点的横坐标是多少?
无公共点
先画出函数图象:
对应一元二次方程的根是多少?
x1 =-2,
x2 =1.
x1 =x2 =3.
方程无解
?
有两个不等实根
有两个相等实根
没有实数根
有两个交点
有一个交点
没有交点
△ > 0
△ = 0
△ < 0
?
抛物线 y=ax2+bx+c与x轴
若抛物线 y=ax2+bx+c 与 x 轴有交点,则
b2 – 4ac ≥ 0
△= b2 – 4ac
二次函数与一元二次方程的关系(2)
?
?
1. 若一元二次方程 无实根,则抛物线 图象位于( )
A.x轴上方 B.第一、二、三象限
C.x轴下方 D.第二、三、四象限
A
三、训练总结
2. 二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3 B.k<3且k≠0
C.k≤3 D.k≤3且k≠0
D
三、训练总结
3.若二次函数y=-x2+2x+k的部分图象如图所示,且关于x的一元二次方程-x2+2x+k=0的一个解x1=3,则另一个解x2= ;
-1
y
O
x
1
3
4. 一元二次方程 3x2+x-10=0的两个根是x1=-2 ,x2= ,那么二次函数 y= 3x2+x-10与x轴的交点坐标是 .
(-2,0) ( ,0)
某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面 米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
能力拓展
四、评点小结
同课章节目录
