人教版八年级数学上册 13.3.1等腰三角形课件(共21张PPT)
文档属性
| 名称 | 人教版八年级数学上册 13.3.1等腰三角形课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 00:00:00 | ||
图片预览



文档简介
等
腰
三
角
形
图片欣赏
感知生活,
从生活走向数学
有两条边相等的三角形叫做等腰三角形。
C
B
回顾概念
A
问题引导,自主学习
A
B
C
D
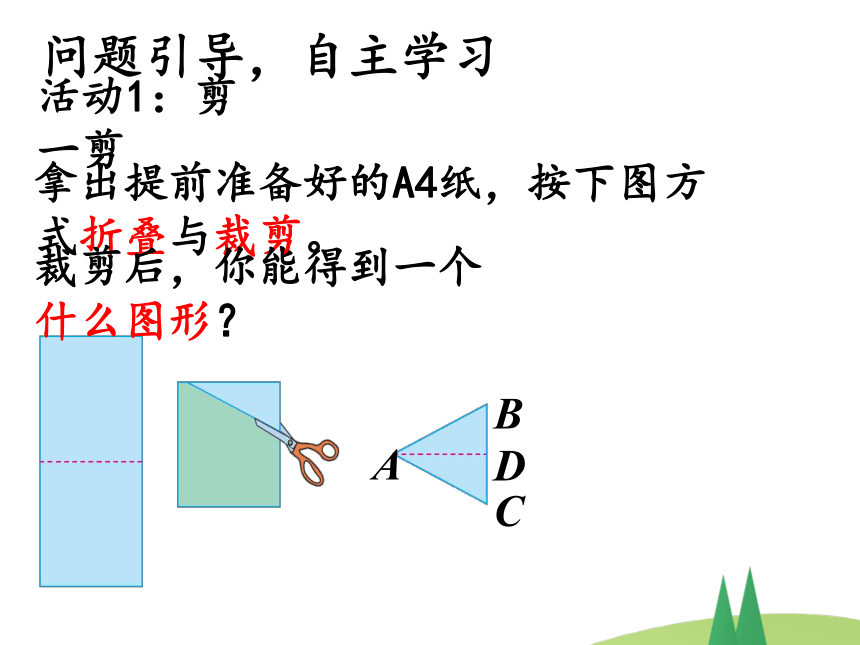
活动1:剪一剪
拿出提前准备好的A4纸,按下图方式折叠与裁剪。
裁剪后,你能得到一个什么图形?
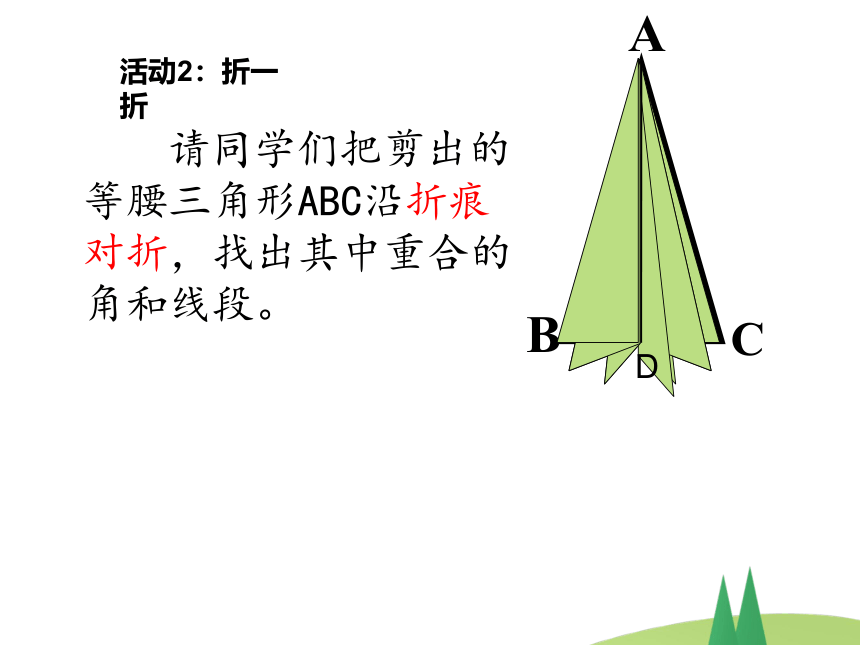
请同学们把剪出的等腰三角形ABC沿折痕对折,找出其中重合的角和线段。
A
B
C
活动2:折一折
D
{5940675A-B579-460E-94D1-54222C63F5DA}重合的角
重合的线段
1、观察第一组重合的角,你发现等腰三角形除了两腰相等,还有什么?
2、观察第二组重合的角,你发现什么?
3、观察第三组重合的角,你发现什么?
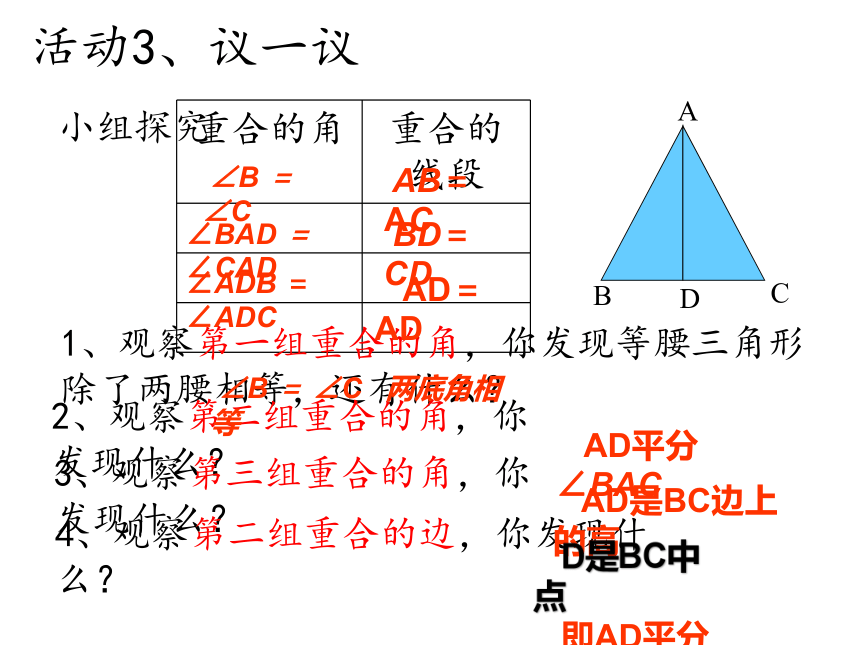
小组探究
活动3、议一议
C
D
A
B
∠B = ∠C
∠BAD = ∠CAD
∠ADB = ∠ADC
AB=AC
BD=CD
AD=AD
4、观察第二组重合的边,你发现什么?
∠B = ∠C 两底角相等
AD平分∠BAC
AD是BC边上的高
D是BC中点
即AD平分BC
猜想:等腰三角形的性质:
性质1:等腰三角形的两个底角相等 (简写为“等边对等角”)
性质2:等腰三角形的顶角平分线、底边上的中线和高线互相重合(简写“三线合一”)
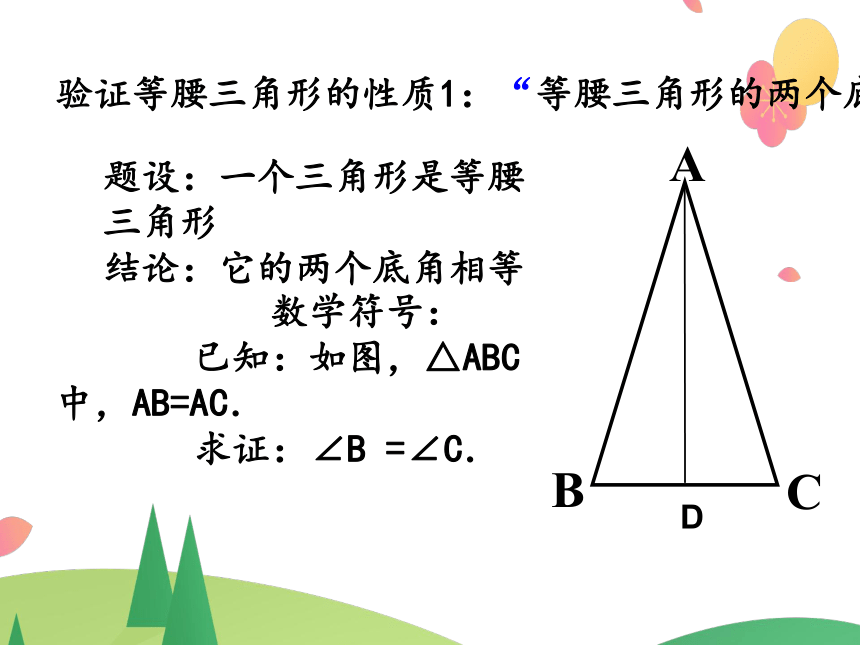
数学符号:
已知:如图,△ABC 中,AB=AC.
求证:∠B =∠C.
A
B
C
D
验证等腰三角形的性质1:“等腰三角形的两个底角相等”
题设:一个三角形是等腰三角形
结论:它的两个底角相等
A
B
C
则有∠1=∠2
D
1
2
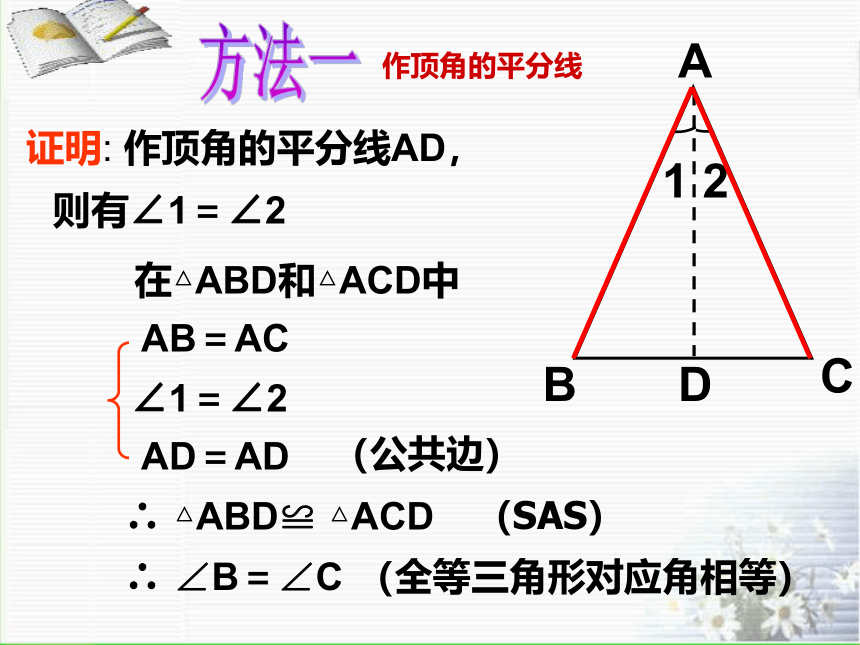
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
作顶角的平分线
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC底边上的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
方法二
A
B
C
则有 ∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC底边上 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
方法三
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
猜想 讨论 论证
猜想:
性质1、等腰三角形的两个底角相等。
(简写成“等边对等角”)
论证
A
B
C
D
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠BDA=∠CDA=90° BD=CD
再探新知
等腰三角形性质2,等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合 (三线合一)
(1) ∵ AD⊥BC,∴ = , =
∠
∠
(3)∵ AD是角平分线, ∴ ,
⊥
=
BAD
CAD
BD
CD
AD
BC
BD
CD
结论:
在等腰三角形中,(在 △ ABC中,AB=AC)
① ∠BAD =∠CAD,② AD ⊥ BC,③ BD = CD
中已知任意一个都可以得其它两个条件.
再创佳绩
在△ABC中,AB=AC 时
(2) ∵ AD是中线, ∴ , =
⊥
∠
∠
BC
BAD
CAD
AD
A
C
B
D
(2)等腰△ABC 中,其中一个角是50°, 则另外两个角的度数是 ;
(1)已知等腰三角形的一个内角为100°,则它的另外两个内角的度数分别是 .
50°、80°或 65°、65°
40°、40°
做一做
(3)等腰三角形的一个内角是另一个内角的2倍,则三个内角分别为:___________________________。
450、450、900
或360、720、720
阶梯训练一
例1.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,
求△ ABC各角的度数
解: ∵AB=AC,BD=BC=AD,
∴ ∠ ABC= ∠ C= ∠ BDC,∠ A= ∠ ABD (等边对等角)。
设∠A=x,则 ∠ BDC= ∠ A+ ∠ ABD=2x,
从而∠ ABC= ∠ C= ∠ BDC=2x.
于是在△ ABC中,有
∠ A+ ∠ ABC+ ∠ C=x+2x+2x=1800.
解得x=360
在△ ABC中, ∠ A=360 ∠ABC= ∠C=720.
等腰三角形性质定理的运用
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
等腰三角形的顶角平分线与底边上的中线,底边上的高相互重合。(简写成“三线合一”)
等腰三角形的性质2
根据等腰三角形性质2,在△ABC中,AB=AC时,
符号语言
(1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
“三线合一”
思考:
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高线,它们是否重合?
不重合!
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高。
为什么?
三线合一
轴对称图形
等腰三角形两个底角相等,简称“等边对等角”
等腰三角形的顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合 一”
等腰三角形
小 结
求有关等腰三角形的问题,作顶角平分线、底边上中线,
底边上的高是常用的辅助线;
谢谢聆听!
腰
三
角
形
图片欣赏
感知生活,
从生活走向数学
有两条边相等的三角形叫做等腰三角形。
C
B
回顾概念
A
问题引导,自主学习
A
B
C
D
活动1:剪一剪
拿出提前准备好的A4纸,按下图方式折叠与裁剪。
裁剪后,你能得到一个什么图形?
请同学们把剪出的等腰三角形ABC沿折痕对折,找出其中重合的角和线段。
A
B
C
活动2:折一折
D
{5940675A-B579-460E-94D1-54222C63F5DA}重合的角
重合的线段
1、观察第一组重合的角,你发现等腰三角形除了两腰相等,还有什么?
2、观察第二组重合的角,你发现什么?
3、观察第三组重合的角,你发现什么?
小组探究
活动3、议一议
C
D
A
B
∠B = ∠C
∠BAD = ∠CAD
∠ADB = ∠ADC
AB=AC
BD=CD
AD=AD
4、观察第二组重合的边,你发现什么?
∠B = ∠C 两底角相等
AD平分∠BAC
AD是BC边上的高
D是BC中点
即AD平分BC
猜想:等腰三角形的性质:
性质1:等腰三角形的两个底角相等 (简写为“等边对等角”)
性质2:等腰三角形的顶角平分线、底边上的中线和高线互相重合(简写“三线合一”)
数学符号:
已知:如图,△ABC 中,AB=AC.
求证:∠B =∠C.
A
B
C
D
验证等腰三角形的性质1:“等腰三角形的两个底角相等”
题设:一个三角形是等腰三角形
结论:它的两个底角相等
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
作顶角的平分线
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC底边上的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
方法二
A
B
C
则有 ∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC底边上 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
方法三
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
猜想 讨论 论证
猜想:
性质1、等腰三角形的两个底角相等。
(简写成“等边对等角”)
论证
A
B
C
D
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠BDA=∠CDA=90° BD=CD
再探新知
等腰三角形性质2,等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合 (三线合一)
(1) ∵ AD⊥BC,∴ = , =
∠
∠
(3)∵ AD是角平分线, ∴ ,
⊥
=
BAD
CAD
BD
CD
AD
BC
BD
CD
结论:
在等腰三角形中,(在 △ ABC中,AB=AC)
① ∠BAD =∠CAD,② AD ⊥ BC,③ BD = CD
中已知任意一个都可以得其它两个条件.
再创佳绩
在△ABC中,AB=AC 时
(2) ∵ AD是中线, ∴ , =
⊥
∠
∠
BC
BAD
CAD
AD
A
C
B
D
(2)等腰△ABC 中,其中一个角是50°, 则另外两个角的度数是 ;
(1)已知等腰三角形的一个内角为100°,则它的另外两个内角的度数分别是 .
50°、80°或 65°、65°
40°、40°
做一做
(3)等腰三角形的一个内角是另一个内角的2倍,则三个内角分别为:___________________________。
450、450、900
或360、720、720
阶梯训练一
例1.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,
求△ ABC各角的度数
解: ∵AB=AC,BD=BC=AD,
∴ ∠ ABC= ∠ C= ∠ BDC,∠ A= ∠ ABD (等边对等角)。
设∠A=x,则 ∠ BDC= ∠ A+ ∠ ABD=2x,
从而∠ ABC= ∠ C= ∠ BDC=2x.
于是在△ ABC中,有
∠ A+ ∠ ABC+ ∠ C=x+2x+2x=1800.
解得x=360
在△ ABC中, ∠ A=360 ∠ABC= ∠C=720.
等腰三角形性质定理的运用
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
等腰三角形的顶角平分线与底边上的中线,底边上的高相互重合。(简写成“三线合一”)
等腰三角形的性质2
根据等腰三角形性质2,在△ABC中,AB=AC时,
符号语言
(1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
“三线合一”
思考:
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高线,它们是否重合?
不重合!
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高。
为什么?
三线合一
轴对称图形
等腰三角形两个底角相等,简称“等边对等角”
等腰三角形的顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合 一”
等腰三角形
小 结
求有关等腰三角形的问题,作顶角平分线、底边上中线,
底边上的高是常用的辅助线;
谢谢聆听!
