人教版九年级数学上册 21.2.1配方法解元二次方程 课件(16张PPT)
文档属性
| 名称 | 人教版九年级数学上册 21.2.1配方法解元二次方程 课件(16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 12:06:20 | ||
图片预览






文档简介
配方法解一元二次方程(二)
课前小练习
温故而知新
1.解下列方程(2分钟)
(1)2x?=8
(2)(x+3)?-25=0
(3)9x?+6x+1=4
直接开平方法
2.你能解下面这个方程吗?
x?+6x+4=0
一元二次方程的解法
——配方法
回顾与复习
温故而知新
3.因式分解的完全平方式,你还记得吗?
完全平方式
填一填
1
4
有什么规律
移项
两边加上32,使左边配成
左边写成完全平方形式
降次
以上解法中,为什么在方程 两边加9?加其他数行吗?
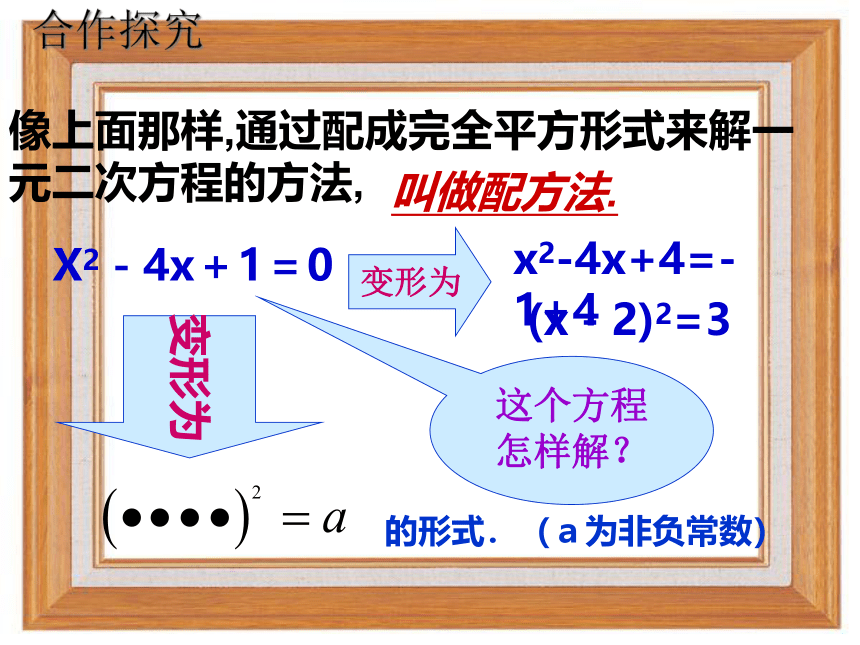
像上面那样,通过配成完全平方形式来解一元二次方程的方法,
叫做配方法.
这个方程怎样解?
变形为
的形式.(a为非负常数)
变形为
X2-4x+1=0
(x-2)2=3
合作探究
x2-4x+4=-1+4
你能行吗
用配方法解一元二次方程的步骤:
1.移项:把常数项移到方程的右边;
2.配方:方程两边都加上一次项系数
绝对值一半的平方;
3.变形:方程左边分解因式,右边合并同类项;
4.开方:
5.求解:解一元一次方程;
6.定解:写出原方程的解.
(x+a)2=b
配方法
例2 解方程 3x2+8x-3=0.
1.化1:把二次项系数化为1;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左边分解因式,右边合并同类项;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
2.移项:把常数项移到方程的右边;
师生合作
练一练:
心动 不如行动
用配方法解方程
回味无穷
本节课你有收获吗?
用配方法解二次项系数不是1的一元二次方程的步骤:
1.化1:把二次项系数化为1(方程两边都除以二次项系数);
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左边分解因式,右边合并同类;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
用一元二次方程这个模型来解答或解决生活中的一些问题(即列一元二次方程解应用题).
小结 拓展
独立
完成
1. 解下列方程:
(1).6x2 -7x+ 1 = 0;
(2).5x2 -9x –18=0;
(3).4x 2 –3x =52;
(4). 5x2 =4-2x.
你能行吗
做一做
一小球以15m/s的初速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:
h=15t-5t2 .
小球何时能达到10m的高度?
开启 智慧
知识的升华
1.印度古算书中有这样一首诗:“一群猴子分两队,高高兴兴在游戏,八分之一再平方,蹦蹦跳跳树林里;其余十二叽喳喳,伶俐活泼又调皮.告我总数共多少”?
解:设总共有 x 只猴子,根据题意得
即
x2 - 64x+768 =0.
解这个方程,得
x1 =48 x2 =16.
答:一共有猴子48只或者说16只.
结束寄语
配方法是一种重要的数学方法——配方法,它可以助你到达希望的顶点.
一元二次方程也是刻画现实世界的有效数学模型.
下课了!
再 见
课前小练习
温故而知新
1.解下列方程(2分钟)
(1)2x?=8
(2)(x+3)?-25=0
(3)9x?+6x+1=4
直接开平方法
2.你能解下面这个方程吗?
x?+6x+4=0
一元二次方程的解法
——配方法
回顾与复习
温故而知新
3.因式分解的完全平方式,你还记得吗?
完全平方式
填一填
1
4
有什么规律
移项
两边加上32,使左边配成
左边写成完全平方形式
降次
以上解法中,为什么在方程 两边加9?加其他数行吗?
像上面那样,通过配成完全平方形式来解一元二次方程的方法,
叫做配方法.
这个方程怎样解?
变形为
的形式.(a为非负常数)
变形为
X2-4x+1=0
(x-2)2=3
合作探究
x2-4x+4=-1+4
你能行吗
用配方法解一元二次方程的步骤:
1.移项:把常数项移到方程的右边;
2.配方:方程两边都加上一次项系数
绝对值一半的平方;
3.变形:方程左边分解因式,右边合并同类项;
4.开方:
5.求解:解一元一次方程;
6.定解:写出原方程的解.
(x+a)2=b
配方法
例2 解方程 3x2+8x-3=0.
1.化1:把二次项系数化为1;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左边分解因式,右边合并同类项;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
2.移项:把常数项移到方程的右边;
师生合作
练一练:
心动 不如行动
用配方法解方程
回味无穷
本节课你有收获吗?
用配方法解二次项系数不是1的一元二次方程的步骤:
1.化1:把二次项系数化为1(方程两边都除以二次项系数);
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左边分解因式,右边合并同类;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
用一元二次方程这个模型来解答或解决生活中的一些问题(即列一元二次方程解应用题).
小结 拓展
独立
完成
1. 解下列方程:
(1).6x2 -7x+ 1 = 0;
(2).5x2 -9x –18=0;
(3).4x 2 –3x =52;
(4). 5x2 =4-2x.
你能行吗
做一做
一小球以15m/s的初速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:
h=15t-5t2 .
小球何时能达到10m的高度?
开启 智慧
知识的升华
1.印度古算书中有这样一首诗:“一群猴子分两队,高高兴兴在游戏,八分之一再平方,蹦蹦跳跳树林里;其余十二叽喳喳,伶俐活泼又调皮.告我总数共多少”?
解:设总共有 x 只猴子,根据题意得
即
x2 - 64x+768 =0.
解这个方程,得
x1 =48 x2 =16.
答:一共有猴子48只或者说16只.
结束寄语
配方法是一种重要的数学方法——配方法,它可以助你到达希望的顶点.
一元二次方程也是刻画现实世界的有效数学模型.
下课了!
再 见
同课章节目录
