人教版七年级上册 3.2解一元一次方程(移项) 课件(15张PPT)
文档属性
| 名称 | 人教版七年级上册 3.2解一元一次方程(移项) 课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 506.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 12:07:57 | ||
图片预览





文档简介
课题:3.2 解一元一次方程(一)
---移项
难点名称:分析问题中的相等关系列出方程
七年级-上册-第三章
目录
CONTENTS
小结
导入
温故知新
1、等式的性质1是什么呢?
等式的两边加(或减)同一个数(或式子),结果仍相等。
2、如何解形如ax+bx=c类型的一元一次方程?
合并同类项
如果a=b,那么a±c=b±c
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
问题:把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
分析:1.设这个班有x名学生
2.找相等关系
难点突破
第一种分法:每人分3本,剩余20本,则这批书共 本;
第二种分法:每人分4本,还缺25本,则这批书共 本.
(3x+20)
(4x-25)
3.列方程
3x+20=4x- 25
这批书有几种分法?
表示同一个量的两个式子相等
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
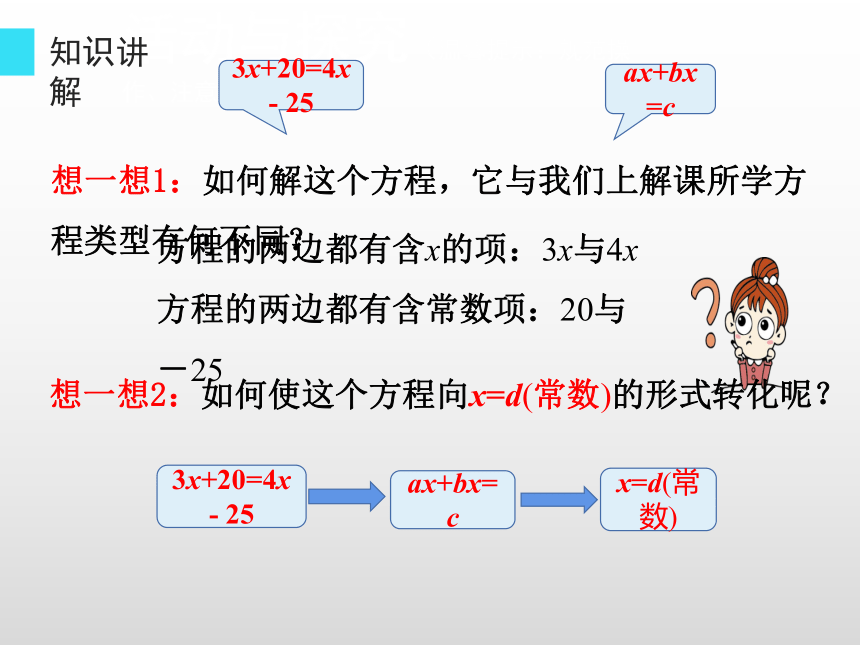
想一想1:如何解这个方程,它与我们上解课所学方程类型有何不同?
3x+20=4x- 25
ax+bx=c
方程的两边都有含x的项:3x与4x
方程的两边都有含常数项:20与-25
3x+20=4x- 25
ax+bx=c
想一想2:如何使这个方程向x=d(常数)的形式转化呢?
x=d(常数)
知识讲解
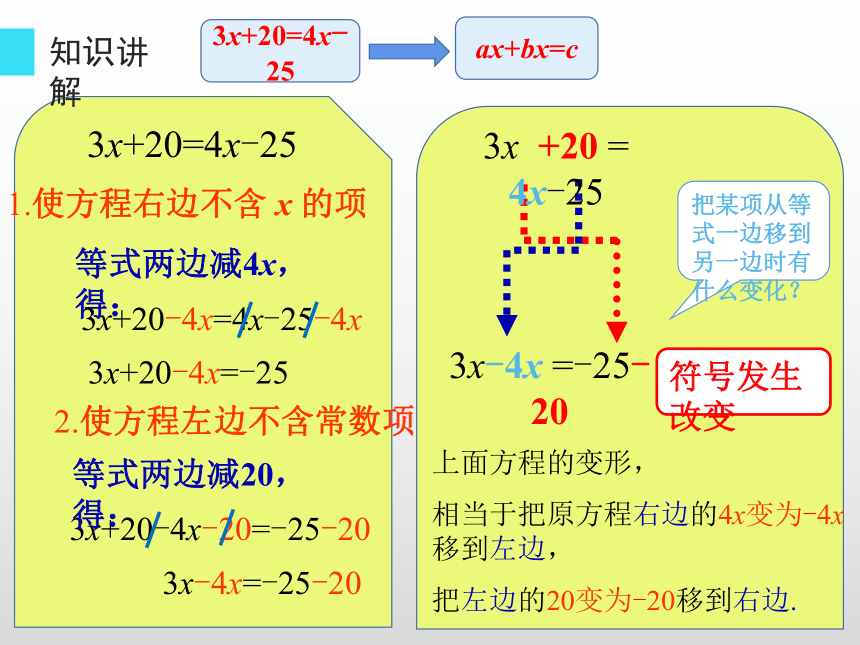
2.使方程左边不含常数项
等式两边减4x,得:
3x+20-4x=4x-25-4x
3x+20-4x=-25
3x+20-4x-20=-25-20
等式两边减20,得:
3x-4x=-25-20
3x+20=4x-25
1.使方程右边不含 x 的项
上面方程的变形,
相当于把原方程右边的4x变为-4x移到左边,
把左边的20变为-20移到右边.
把某项从等式一边移到另一边时有什么变化?
3x +20 = 4x-25
3x-4x =-25-20
3x+20=4x-25
ax+bx=c
符号发生改变
等式的性质1.
知识讲解
把等式一边的某项变号后移到另一边,叫做移项.
通过移项,将含有未知数的项移到方程的
一边,将常数项移到方程的另一边,使方
程更接近 x=a 的形式.
定义
思考1:移项的依据是什么?
思考2:上面解方程中“移项”起了什么作用?
知识讲解
下面的框图表示了解这个方程的流程
移项
合并同类项
系数化为1
由上可知,这个班有45名学生.
移项
要变号
知识讲解
例题讲解
例1:填一填,把下列方程移项可得:
(1)3x-4=5
移项
移项
(2)6x+3=2x-5
3x=5 +4
6x-2x=-5-3
移项
要变号
移项时需要移哪些项?
课堂练习
10
练习1:判断下列移项是否正确:
针对训练
×
×
√
×
×
知识讲解
例题讲解
例2:解下列方程:
解:移项,得
系数化为1,得
(1)
合并同类项,得
解:移项,得
合并同类项,得
系数化为1,得
(2)
解:移项,得
合并同类项,得
系数化为1,得
课堂练习
12
针对训练
练习2:解下列方程:
(1) 6x-7=4x-5
(2)
解:移项,得
6x-4x=-5+7
合并同类项,得
2x=2
系数化为1,得
x=1
课堂练习
13
练习3:几个人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种;如果每人种12棵,则缺6棵树苗.求参与种树的人数.
针对训练
难点巩固
解:设有x人参加种树,根据题意可得:
10x+6=12x-6
移项,得
10x-12x=-6-6
合并同类项,得
-2x=-12
系数化为1,得
x=6
答:共有6人参加种树.
寻找
相等关系
表示同一个量的两个式子相等
【课堂小结】
小结
移项解
一元一次方程
定义
步骤
应用
注意:移项一定要变号
移项
合并同类项
系数化为1
这节课我们学习了什么?
分配问题
---移项
难点名称:分析问题中的相等关系列出方程
七年级-上册-第三章
目录
CONTENTS
小结
导入
温故知新
1、等式的性质1是什么呢?
等式的两边加(或减)同一个数(或式子),结果仍相等。
2、如何解形如ax+bx=c类型的一元一次方程?
合并同类项
如果a=b,那么a±c=b±c
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
问题:把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
分析:1.设这个班有x名学生
2.找相等关系
难点突破
第一种分法:每人分3本,剩余20本,则这批书共 本;
第二种分法:每人分4本,还缺25本,则这批书共 本.
(3x+20)
(4x-25)
3.列方程
3x+20=4x- 25
这批书有几种分法?
表示同一个量的两个式子相等
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
想一想1:如何解这个方程,它与我们上解课所学方程类型有何不同?
3x+20=4x- 25
ax+bx=c
方程的两边都有含x的项:3x与4x
方程的两边都有含常数项:20与-25
3x+20=4x- 25
ax+bx=c
想一想2:如何使这个方程向x=d(常数)的形式转化呢?
x=d(常数)
知识讲解
2.使方程左边不含常数项
等式两边减4x,得:
3x+20-4x=4x-25-4x
3x+20-4x=-25
3x+20-4x-20=-25-20
等式两边减20,得:
3x-4x=-25-20
3x+20=4x-25
1.使方程右边不含 x 的项
上面方程的变形,
相当于把原方程右边的4x变为-4x移到左边,
把左边的20变为-20移到右边.
把某项从等式一边移到另一边时有什么变化?
3x +20 = 4x-25
3x-4x =-25-20
3x+20=4x-25
ax+bx=c
符号发生改变
等式的性质1.
知识讲解
把等式一边的某项变号后移到另一边,叫做移项.
通过移项,将含有未知数的项移到方程的
一边,将常数项移到方程的另一边,使方
程更接近 x=a 的形式.
定义
思考1:移项的依据是什么?
思考2:上面解方程中“移项”起了什么作用?
知识讲解
下面的框图表示了解这个方程的流程
移项
合并同类项
系数化为1
由上可知,这个班有45名学生.
移项
要变号
知识讲解
例题讲解
例1:填一填,把下列方程移项可得:
(1)3x-4=5
移项
移项
(2)6x+3=2x-5
3x=5 +4
6x-2x=-5-3
移项
要变号
移项时需要移哪些项?
课堂练习
10
练习1:判断下列移项是否正确:
针对训练
×
×
√
×
×
知识讲解
例题讲解
例2:解下列方程:
解:移项,得
系数化为1,得
(1)
合并同类项,得
解:移项,得
合并同类项,得
系数化为1,得
(2)
解:移项,得
合并同类项,得
系数化为1,得
课堂练习
12
针对训练
练习2:解下列方程:
(1) 6x-7=4x-5
(2)
解:移项,得
6x-4x=-5+7
合并同类项,得
2x=2
系数化为1,得
x=1
课堂练习
13
练习3:几个人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种;如果每人种12棵,则缺6棵树苗.求参与种树的人数.
针对训练
难点巩固
解:设有x人参加种树,根据题意可得:
10x+6=12x-6
移项,得
10x-12x=-6-6
合并同类项,得
-2x=-12
系数化为1,得
x=6
答:共有6人参加种树.
寻找
相等关系
表示同一个量的两个式子相等
【课堂小结】
小结
移项解
一元一次方程
定义
步骤
应用
注意:移项一定要变号
移项
合并同类项
系数化为1
这节课我们学习了什么?
分配问题
