人教版数学八年级上册12.3探究角平分线的性质课件(第2课时 共16张PPT)
文档属性
| 名称 | 人教版数学八年级上册12.3探究角平分线的性质课件(第2课时 共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 339.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 08:21:29 | ||
图片预览


文档简介
角的平分线的性质
新人教版 八年级 上册
(第2课时)
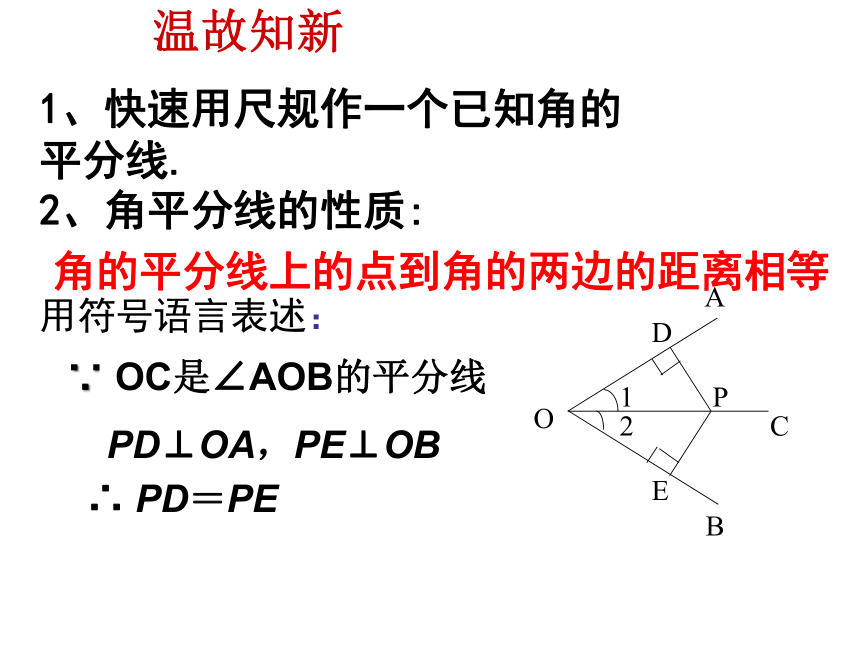
1、快速用尺规作一个已知角的平分线.
角的平分线上的点到角的两边的距离相等
2、角平分线的性质:
O
C
B
1
A
2
P
D
E
PD⊥OA,PE⊥OB
∵ OC是∠AOB的平分线
∴ PD=PE
用符号语言表述:
温故知新
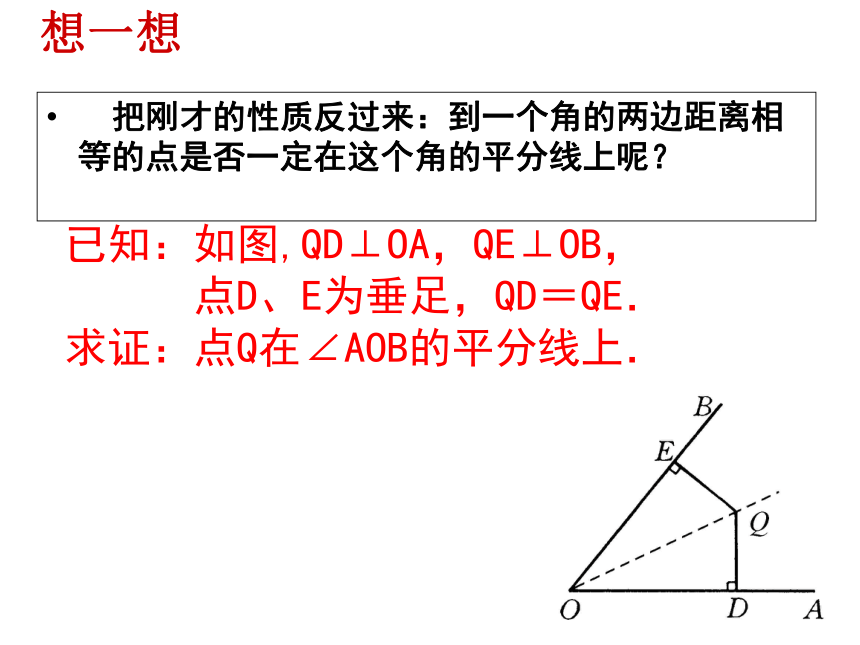
把刚才的性质反过来:到一个角的两边距离相等的点是否一定在这个角的平分线上呢?
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
想一想
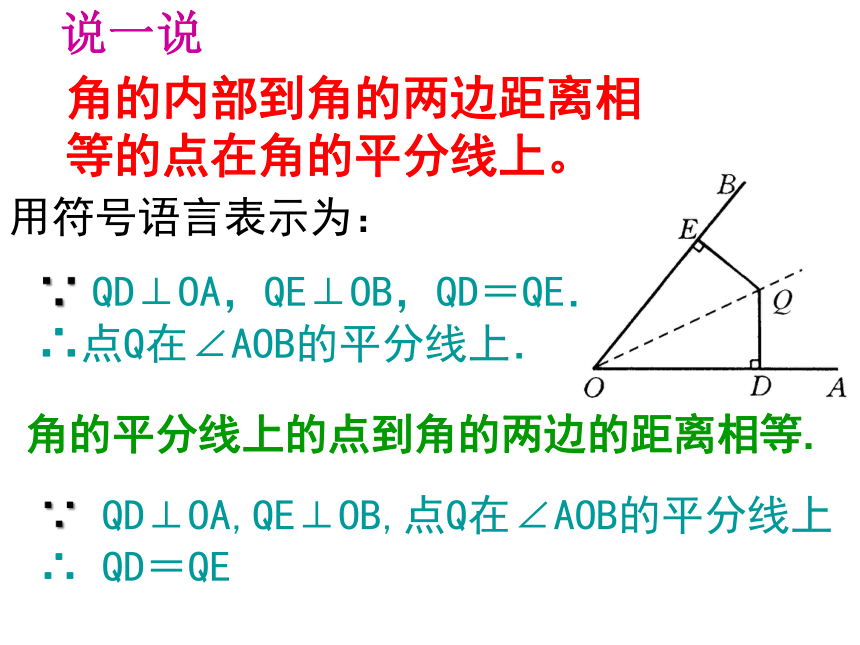
角的内部到角的两边距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用符号语言表示为:
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
说一说
所以:
角平分线可以看做到角的两边距离相等的所有点的集合
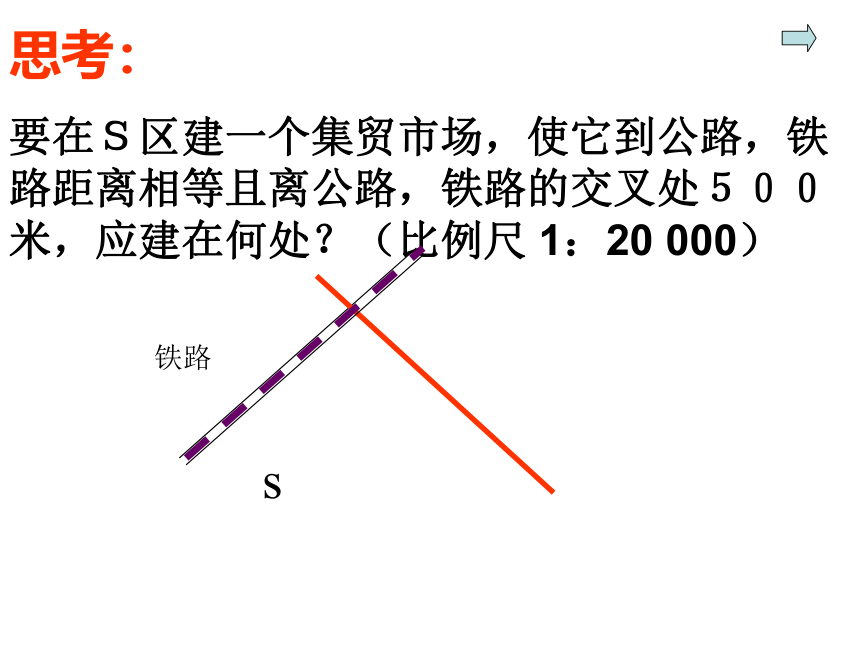
思考:
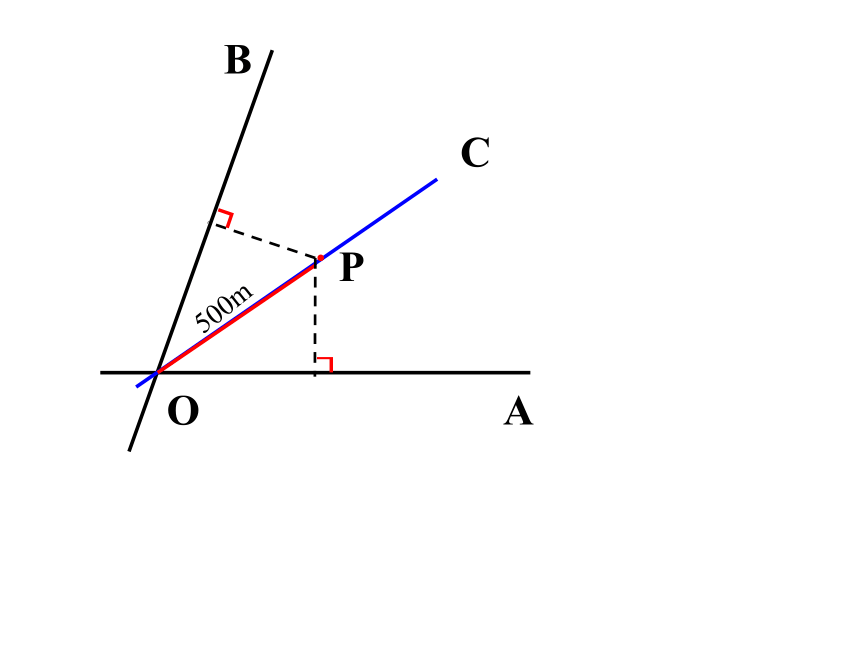
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)
s
O
公路
铁路
·
O
A
B
C
P
500m
┒
┓
例 已知:如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
学习例题
走进生活
1、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
想一想
在确定度假村的位置时,一定要画出三个角的平分线吗?你是怎样思考的?你是如何证明的?
2、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( )
A.一处 B. 两处
C.三处 D.四处
分析:由于没有限制在何处选址,故要求的地址共有四处。
丰收乐园
将你今天的收获与大家共同分享吧!
到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
角平分线可以看做到角的两边距离相等的 所有点的集合
某一个星期六,二十一中初一年级的同学参加义务劳动,其中有四个班的同学分别在M、N两处参加劳动,另外四个班的同学分别在道路AB、AC两处劳动,现要在道路AB、AC的交叉区域内设一个荼水供应点P,使P到两条道路的距离相等,且使PM=PN,请你找出点P的位置,并说明理由。
A
·M
B
·N
C
综合应用
P
2、如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
G
H
M
3、如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
A
B
C
E
F
D
再见
新人教版 八年级 上册
(第2课时)
1、快速用尺规作一个已知角的平分线.
角的平分线上的点到角的两边的距离相等
2、角平分线的性质:
O
C
B
1
A
2
P
D
E
PD⊥OA,PE⊥OB
∵ OC是∠AOB的平分线
∴ PD=PE
用符号语言表述:
温故知新
把刚才的性质反过来:到一个角的两边距离相等的点是否一定在这个角的平分线上呢?
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
想一想
角的内部到角的两边距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用符号语言表示为:
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
说一说
所以:
角平分线可以看做到角的两边距离相等的所有点的集合
思考:
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)
s
O
公路
铁路
·
O
A
B
C
P
500m
┒
┓
例 已知:如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
学习例题
走进生活
1、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
想一想
在确定度假村的位置时,一定要画出三个角的平分线吗?你是怎样思考的?你是如何证明的?
2、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( )
A.一处 B. 两处
C.三处 D.四处
分析:由于没有限制在何处选址,故要求的地址共有四处。
丰收乐园
将你今天的收获与大家共同分享吧!
到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
角平分线可以看做到角的两边距离相等的 所有点的集合
某一个星期六,二十一中初一年级的同学参加义务劳动,其中有四个班的同学分别在M、N两处参加劳动,另外四个班的同学分别在道路AB、AC两处劳动,现要在道路AB、AC的交叉区域内设一个荼水供应点P,使P到两条道路的距离相等,且使PM=PN,请你找出点P的位置,并说明理由。
A
·M
B
·N
C
综合应用
P
2、如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
G
H
M
3、如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
A
B
C
E
F
D
再见
